不同路径

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1, vector<int>(n+1,0));//创建dp表dp[0][1] = 1;//初始化//填表for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];}
};
不同路径II

代码一
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {//创建dp表int m = obstacleGrid.size(),n = obstacleGrid[0].size();vector<vector<int>> dp(m + 1, vector<int>(n+1, 0));dp[0][1] = 1;//初始化//填表for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(i >= 2 && obstacleGrid[i-1-1][j-1] == 1) dp[i-1][j] =0;if(j >= 2 && obstacleGrid[i-1][j-1-1] == 1) dp[i][j-1] =0;dp[i][j] = dp[i-1][j] + dp[i][j-1];if(obstacleGrid[i-1][j-1] == 1) dp[i][j] =0;//终点存在障碍}}return dp[m][n];}
};
代码二
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {//创建dp表int m = obstacleGrid.size(),n = obstacleGrid[0].size();vector<vector<int>> dp(m + 1, vector<int>(n+1, 0));dp[0][1] = 1;//初始化//填表for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)if(obstacleGrid[i-1][j-1] == 0)dp[i][j] = dp[i-1][j] + dp[i][j-1];return dp[m][n];}
};
以上代码一可以返回正确答案;但存在错误修改闲置背包问题,逻辑思维不严谨;
这道题只需要在上道题的基础上加一个障碍物判断即可,代码实现也是如此。
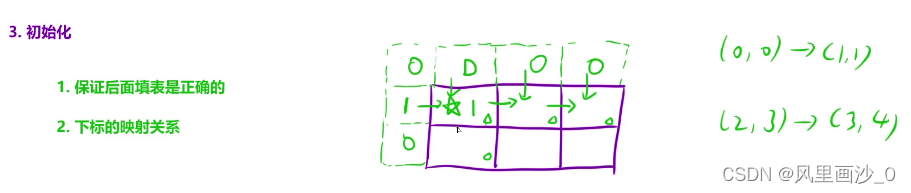
注意:注意这里的映射关系
obstacleGrid[i-1-1][j-1]对应的位置应是dp[i-1][j];<这里的映射关系非常重要>












:按键控制实验)

——综合案例)

页面渲染完成后让输入框自动获取焦点)


C++自制植物大战僵尸游戏客户端更新实现)

