HMM（Hidden Markov Model）是一种统计模型，用来描述一个隐含未知量的马尔可夫过程（马尔可夫过程是一类随机过程，它的原始模型是马尔科夫链），它是结构最简单的动态贝叶斯网，是一种著名的有向图模型，主要用于时序数据建模。在语音识别、自然语言处理等领域有广泛应用

Background requirements：

1、基础的概率学知识

2、动态规划是加分项

3、有实际运用Markov Model的应用会帮助学以致用

NOTE：

对于下面的介绍，我们依据这个节奏，参考。

1）指定模型参数

2）如何估计这些参数 【这个没有进行介绍】

3）利用这些参数进行预测

这三大类适用于任何统计机器学习模型

马尔可夫模型（Markov Model）是一种统计模型，广泛应用在语音识别，词性自动标注，音字转换，概率文法、序列分类等各个自然语言处理等应用领域。经过长期发展，尤其是在语音识别中的成功应用，使它成为一种通用的统计工具。到目前为止，它一直被认为是实现快速精确的语音识别系统的最成功的方法之一。

二、马尔科夫模型的案例之一——天气预报
下面是一个马尔科夫模型在天气预测方面的简单例子。如果第一天是雨天，第二天还是雨天的概率是0.8，是晴天的概率是0.2；如果第一天是晴天，第二天还是晴天的概率是0.6，是雨天的概率是0.4。问：如果第一天下雨了，第二天仍然是雨天的概率是多少？，第十天是晴天的概率是多少？；经过很长一段时间后雨天、晴天的概率分别是多少？

首先构建转移概率矩阵，由于这里每一天的状态就是晴天或者是下雨两种情况，所以矩阵是2x2的，如下：

雨天	晴天
0.8	0.4	雨天
0.2	0.6	晴天

注意：每列和为1，分别对雨天、晴天，这样构建出来的就是转移概率矩阵了。如下：

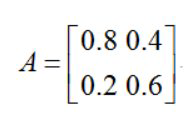
假设初始状态第一天是雨天，我们记为

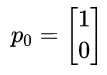
这里【1，0】分别对于雨天，晴天。

初始条件：第一天是雨天，第二天仍然是雨天（记为P1）的概率为：

P1 = AxP0

得到P1 = 【0.8,0.2】，正好满足雨天~雨天概率为0.8，当然这根据所给条件就是这样。

下面计算第十天（记为P9）是晴天概率：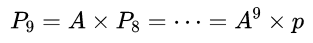

得到，第十天为雨天概率为0.6668，为晴天的概率为0.3332。

下面计算经过很长一段时间后雨天、晴天的概率，显然就是下面的递推公式了：

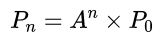
2.2 递推公式的改进

虽然上面构造了一个递推公式，但是直接计算矩阵A的n次方是很难计算的，我们将A进行特征分解（谱分解）一下，得到：

现在递推公式变成了下面的样子：

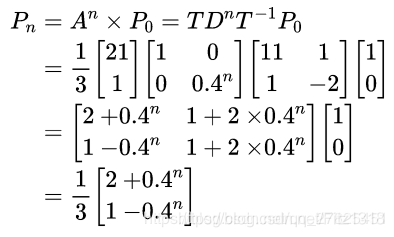
显然，当n趋于无穷即很长一段时间以后，Pn = 【0.67，0.33】。即雨天概率为0.67，晴天概率为0.33。并且，我们发现：初始状态如果是P0 =【0，1】，最后结果仍然是Pn = 【0.67，0.33】。这表明，马尔科夫过程与初始状态无关，跟转移矩阵有关。

一文带你了解隐马尔可夫模型（含详细推导） - 知乎