一.数组：

1.数组的地址计算：

数组的地址计算比较简单，读者可以自行了解，在这里不再赘述；

2.特殊矩阵的压缩存储：

 在这里我们主要说明稀疏矩阵的主要内容：

（1）稀疏矩阵的三元组表示法：

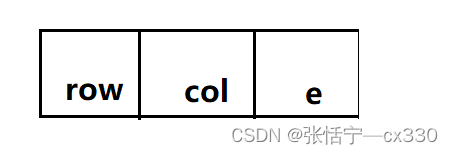
在这里，存放非零元素的行标，列标以及元素值：

三元组表存放在一维数组中，一行一行存储，并且在每一行中，按照列号递增的方式来 ！

（2）稀疏矩阵的三元组表的定义：

#define MAXSIZE 1000#define ElementType int
typedef struct
{int row, col;//定义行标，列标ElementType e;
}Triple;typedef struct//定义矩阵
{Triple data[MAXSIZE];int m, n, len;//矩阵的行，列数，以及非零元素的个数；
}TSmatrix;

 （3）矩阵的转置算法

a.经典的矩阵转置：

//经典的矩阵转置算法：就是给出矩阵及其转置矩阵，对应位置直接赋值void TransMatrix(ElementType source[m][n], ElementType dest[n][m])（二维的）
{int i, j;for (i = 0; i < m; i++){for (j = 0; j < n; j++){dest[j][i] = source[i][j];}}
}

b.用三元组实现稀疏矩阵的转置：

关键点：保证转置之后的三元组也是按照行序优先来进行存储的

那么如果说先直接交换行列的值，那么就会造成转换之后的顺序紊乱，如果要保证转置之后仍然按照行优先来进行存储，那么我们需要对其按照行优先进行排序，就会移动大量的元素；

为了解决上述问题：

（1）列序递增转置算法

假设A为要转置的三元组表，B为最终结果的存放；

列序递增即按照A的列号进行递增排列存储的算法；

依次扫描A的列，每一个分别找出列号为1-K的，找到后就存入B中；

在这里：可能会有读者有这样的疑问：我们已经按照A的列号进行递增存贮，我们是否还需要对A的行号进行比较判断呢?以保证转置之后的的元素按照“列序”递增的顺序进行排列

答案是否定的，在转置之前，A就是按照行号递增来进行排序的，那么我们一定是先找到行号比较小的符合条件的元素，所以不需要再对行号进行排序；

//稀疏矩阵的列序递增转置算法void TransposeTSMatrix(TSmatrix A, TSmatrix* B)//B传址调用
{int i, j, k;//先对B的行列数，以及元素个数进行初始化B->m = A.n;B->n = A.m;B->len = A.len;if (B->len > 0){j = 0;for (k = 1; k <= A.n; k++)//扫描A，找到列数等于K的元素{for (i = 1; i < A.len; i++)//对三元组表中所有的元素进行遍历{if (A.data[i].col == k){B->data[j].row = A.data[i].col;B->data[j].col = A.data[i].row;B->data[j].e = A.data[i].e;j++;}}}}
}

算法的时间复杂度分析：算法的时间耗费主要是在双重循环中，时间复杂度为：O（A.n*A.len)

A.len最大为A.m*A.n，此时算法时间复杂度为：O（A.m*A.n^2），而经典的算法实现转置的时间复杂度为：O(A.m*A.n)

由此可见：采用列序递增的算法，储存空间减少，但是在非零元素的个数较多时，时间复杂度并未显著降低；

（2）一次定位快速转置算法

一次定位快速转置：为了降低上述过程的时间复杂度；

那么我们需要以牺牲空间为代价：引入num[]，和position[]这两个数组

其中num[]用于存放每一列的非零元素的总个数，position数组用于存放每一列的第一个非零元素对应在B中应该存放的位置，即在B三元组中的下标；

num[col]：扫描一遍三元组表A，A的元素的列标出现一次，num[col]就增加1，最终得到相应的列标对应的总的非零元素的个数；

position[col]：根据上述position其实就是表示对应元素在B中应该存放的下标的值；那么position[col]=position[col-1]+num[col-1]，即上一列的下标，加上上一列的总的元素所占的位置，就是这一列的首非零元的在B中的下标；

在算法实现中：我们首先将num初始化为0，并且遍历一次A，求出相应的num数组；

其次我们应该利用：position[col]=position[col-1]+num[col-1]，这个语句来计算列对应的position的值，并且由于存在col-1,而col是从1开始的，而第一个存储的元素的在B中的下标一定为1，那么我们可以直接将position[1]=1即可；然后就可以从A的列标为2，开始遍历，计算position[col]；在这里是给position赋值，所以不用初始化为0；

关于B中的对应的下标的移动：在不同的列中，是通过position来进行增加移动的；

那在相同的列中呢？我们可以在相同的列中，每存储到B中一个元素，就把对应的列position[col]++，然后就可以使得position[col]一直都指向即将要存储的正确位置了；

最后，再次遍历A，将A的行列以及元素值都赋给B，每赋一个，就把对应的position[col]++，更新位置即可！（只要能够理解num和position的实现，就能够理解快速转置算法啦！）

以下是具体的代码实现：

void FastTransposeTSMatrix(TSmatrix A, TSmatrix *B)
{int col, t, p, q;//列标int num[MAXSIZE], position[MAXSIZE];//仍然是先初始化B的行列数以及非零元素值B->len = A.len;B->n = A.m;B->m = A.n;if (B->len > 0){for (col = 1;col <= A.n; col++){num[col] = 0;//先将num数组初始化为0；//且数组是从1开始的！}//接着遍历A中的所有元素for (t = 1; t < A.len; t++){num[A.data[t].col]++;//A中的元素的列标作为num的下标；}position[1] = 1;//第一个肯定是存储在第一个位置//那么从第二列开始赋值；for (col = 2; col <= A.n; col++){position[col] = position[col - 1] + num[col - 1];}for (p = 1; p <= A.len; p++){col = A.data[p].col;//列数取决于A中的元素的列数q = position[col];//q一直是在B中的下标；B->data[q].row = A.data[p].col;//B的行等于A的列；B->data[q].col = A.data[p].row;B->data[q].e = A.data[p].e;position[col]++;//下一个元素依然可能是这个列，因此改变下标位置；而不是这个列，对应的也有新的position值，所以....}}
}

一次定位快速转置的时间复杂度：在这里时间主要耗费在4个并列的单循环上；分别为：O(A.len)+O(A.n)+O（A.len)+O(A.n)，那么该算法的时间复杂度就为：O（A.n+A.len)

那么我们总结一下：按照列序递增的方式与一次定位的区别：

按照列序递增，遍历K次A，按照列号递增，每次找到对应的列号的运算，再存入到B中，也就是必须是依次存放，列号要么相等，要么相邻；

而对于一次定位快速转置来说：遍历一次，不用非要是挨着的或者是一样的列标一次存入，按照列标存入到对应的应该存放的位置，不一定非要连续存入，其实更像是插入；一次定位的关键也就在这，就是要找到列标对应的正确的存放位置，也就是上述所说的position[col]的计算；

---

以上就是关于稀疏矩阵快速转置的算法理解，欢迎大家在评论区进行交流！