怎么把Python当计算器用？(小白自学笔记)

Part I：标准数学包的导入

        今天刚刚装了python，打算用它来取代matlab的基本计算功能，当我的日常计算器用。(这里还有一个捷径，如果你跟我一样也是纯小白的话，直接问chatGPT就好了。。。关于python的常见问题，基本上他啥都知道。)

首先在python的官方文档中找到对应的标准数学库中函数的说明：

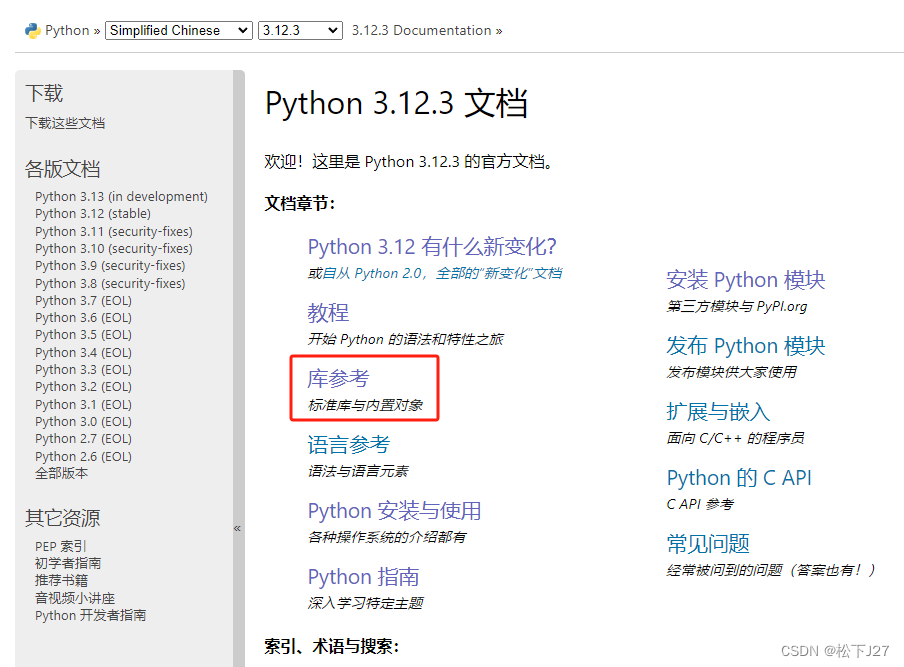
打开以后往下划拉，找到这一块：

打开以后就是各种常用的基础计算函数：

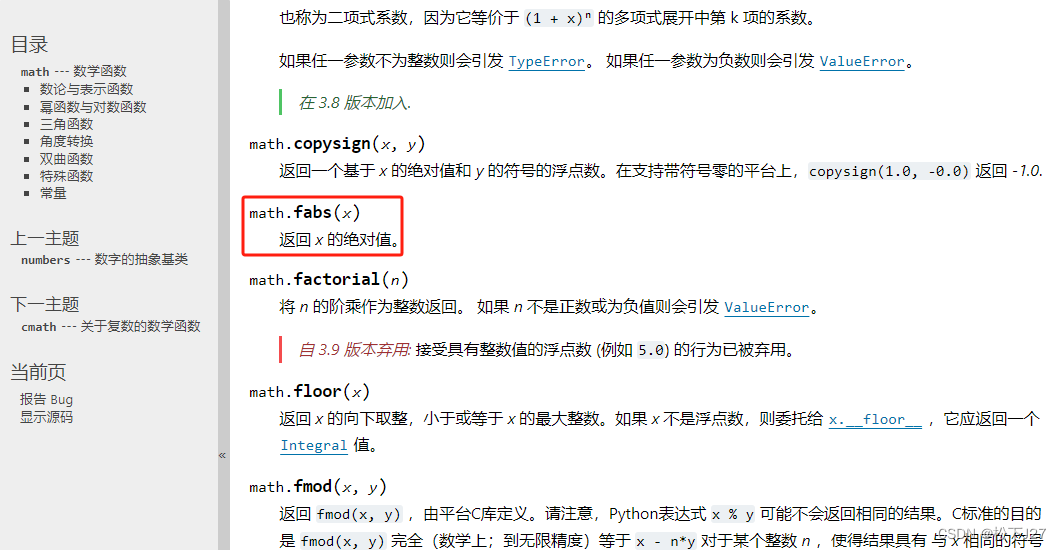
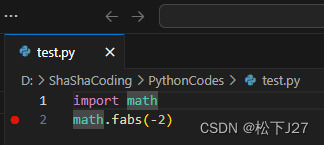
在我们的VS code中试一试这个求绝对值的函数。如图我按照官方函数的说明求“-2”的绝对值，然后单击右上角的"Run"。

运行报错：

 ‘math’没有定义。此外，我们还可以点击“PROBLEMS”，看看里面的详细错误提示。

        根据NameError后面的提示，他说，“did you forget to import ‘something’”。后面我才知道，如果要使用python自带的标准数学库math。需要先import(导入)这个math库。感觉这一点有点类似于C语言编程中的include xxx。

下面改写code如下：

 Line1: 导入数学库。

Line 2:把计算结果赋值给变量a。

Line3:使用了print函数打印计算结果，结果保存在变量a中。

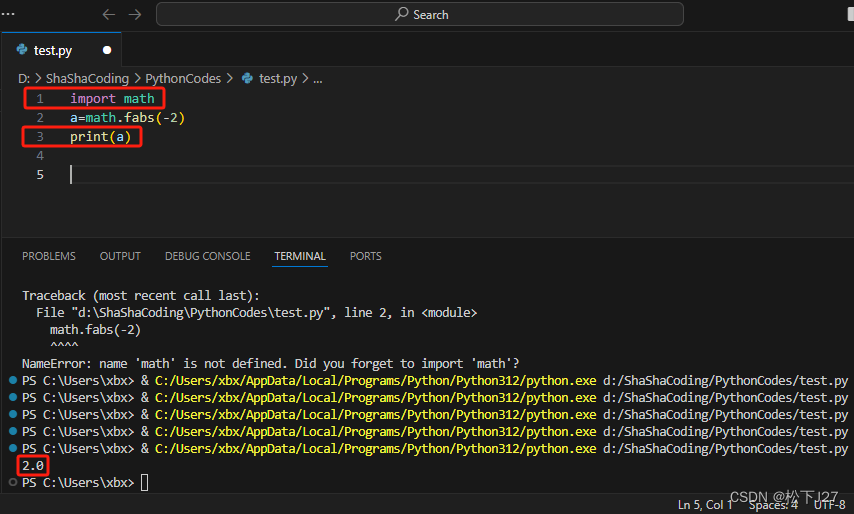
好了，现在可以把python当成计算器用了，但是还有一点就是你无法在命令行中输入带有函数的命令，只能在编译窗口中输入才行。比如说，下面的做法是行不通的：

但可以做简单的计算，比如：

---

Part II：标准数学包的使用

幂函数

幂函数(底是变量):是一个以变量为底数，以常数作为指数的函数。

其中 x 是变量，a是常数，表示a个未知数相乘的结果。

x的平方与x的立方：" x**2 "

#J27@CSDN 2024/04/11
import math#power
x=2
a2=x**2
b3=x**3
print("squre of a =",a2)
print("the cube of b =",b3)

x的平方根与立方根： "math.sqrt(x)"

a=math.sqrt(a2)
b=math.cbrt(b3)
print("sqrt=",a)
print("cbrt=",b)

平方根和立方根是前面的逆运算，得到结果都是2.

---

指数函数

指数函数(指数是变量):是一个以常数为底数，以变量作为指数的函数。

 

其中， a 是常数，x 是变量。表示未知数个a连乘的结果。

a的x次幂：" a**x "

#exponentinal
print("for x > 1:")
base=2
x=2
a=base**(x)
print("2 to the power of x =",a)
x=7
b=base**(x)
print("2 to the power of x =",b)
print("\n")

a的x次方根："a**x" 

print("for x < 1:")
base=2
x=1/2
a=base**(x)
print("2 to the power of x =",a)
x=1/3
b=base**(x)
print("2 to the power of x =",b,"\n")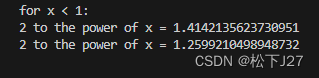

---

自然指数函数

自然指数函数(指数是变量):是以欧拉数e为底数，以变量x为指数的函数。

 

其中， e是常数，x是变量。表示未知数个e连乘的结果。

 e的x次幂："math.exp(x)"

#natural exponentinal
print("base = e")
x=1
a=math.exp(x)
print("e =",a)
x=10
b=math.exp(x)
print("e to the power of x =",b)
x=1
c=math.sqrt(math.exp(x))
print("squre root of e =",c)
print("\n")

e的x次方减1："math.expm1(x)"

        这是在连续复利的情况下计算有效年利率的计算公式，听起来很绕对吧。我也是前段时间才刚刚给自己科普过。

复利――定期复利https://www.shuxuele.com/money/compound-interest-periodic.html

        不懂也不要紧，反正这是python里面自带的一个函数，他可以用exp(x)-1的结果来代替。

#Effective annual rate
x=0.08
a=math.expm1(x)
print("Effective annual rate of 8% =",a)
b=math.exp(x)-1
print("Effective annual rate of 8% =",b)
print("\n")

---

 对数函数

对数是幂的逆运算:

 

读作：x以b为底的对数是y。 

比如说，幂运算要我们求2的三次方等于多少？8。对数运算问的就是，多少个2相乘才等于8呢？3。

这是幂运算： 

这是对数运算：

读作：8以2为底的对数是多少？ 

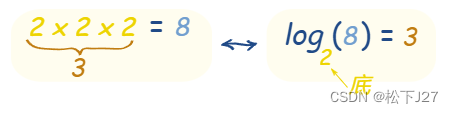
 x以2为底的对数："math.log2(x)"

#logarithm
x=8
a=math.log2(x)
print("log base 2 of 8 = ",a)
print("\n")

 x以10为底的对数："math.log10(x)"

x=50
a=math.log10(x)
print("log base 10 of 50 = ",a)
print("\n")

 x以e为底的对数："math.log(x)"

x=3
a=math.log(x)
print("log base e of 3 = ",a)
print("\n")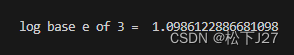

 x以任意数为底的对数："math.log(x，base)"

他的计算结果等于换底公式的计算结果，也就是说， math.log(x，base)可以用math.log(x)/math.log(base)来替换，他们两个是等价的。

base=5
x=3125
a=math.log(x,base)
print("log base 5 of 3125 = ",a)
b=math.log(x)/math.log(base)
print("log(x)/log(base) = ",a)
print("\n")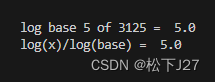

---

两个常量

pi:"math.pi"

print("pi = ",math.pi)
print("\n")

e:"math.e"

print("e = ",math.e)
print("\n")

---

 （全文完）

作者 --- 松下J27 

参考文献：

1，math --- 数学函数 — Python 3.12.3 文档

2，Introduction to Logarithms

3，指数与对数

版权声明：文中的部分图片，文字或者其他素材，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27