这篇文章我们来讲解一下数据结构中非常重要的B-树。
目录
1.B树的相关介绍
1.1、B树的介绍
1.2、B树的特点
2.B树的节点类
3.小结
1.B树的相关介绍
1.1、B树的介绍
在介绍B树之前,我们回顾一下我们学的树。
首先是二叉树,这个不用多说,然后为了查找的效率,我们提出了搜索二叉树(或者称为二叉搜索树),就是节点类加个key值,然后左边小右边大的那个。然后为了避免极端情况的出现,就是二叉搜索树节点集中在一侧的情况,我们提出了平衡二叉树,就是带自旋的,可以左旋或者右旋的,高度差小于1的那种,平衡二叉树里面有AVL树和红黑树两种实现方式,注意,平衡二叉树是在二叉搜索树的基础上提出的,所以平衡二叉树也叫平衡二叉搜索树。
下面介绍一下B树。
B-树是一种自平衡的多路查找树,注意: B树就是B-树,"-"是个连字符号,不是减号 。
在大多数的平衡查找树(Self-balancing search trees),比如 AVL树 和红黑树,都假设所有的数据放在主存当中。那为什么要使用 B-树呢(或者说为啥要有 B-树呢)?要解释清楚这一点,我们假设我们的数据量达到了亿级别,主存当中根本存储不下,我们只能以块的形式从磁盘读取数据,与主存的访问时间相比,磁盘的 I/O 操作相当耗时,而提出 B-树的主要目的就是减少磁盘的 I/O 操作。
大多数平衡树的操作(查找、插入、删除,最大值、最小值等等)需要 O(ℎ)次磁盘访问操作,其中 ℎ 是树的高度。但是对于 B-树 而言,树的高度将不再是log(n)(n为数中节点的个数),而是一个我们可控的高度 ℎ (通过调整 B-树中结点所包含的键【你也可以叫做数据库中的索引,本质上就是在磁盘上的一个位置信息】的数目,使得 B-树的高度保持一个较小的值)。一般而言,B-树的结点所包含的键的数目和磁盘块大小一样,从数个到数千个不等。由于B-树的高度 h 可控(一般远小于log(n)),所以与 AVL 树和红黑树相比,B-树的磁盘访问时间将极大地降低。
我们之前谈过红黑树与AVL树相比较,红黑树更好一些,这里我们将红黑树与B-树进行比较,并以一个例子对上面一段的内容进行解释。
假设我们现在有 838,8608 条记录,对于红黑树而言,树的高度 ℎ=log(838,8608)=23 ,也就是说树的高度为23,也就是说如果要查找到叶子结点需要 23 次磁盘 I/O 操作;但是 B-树,情况就不同了,假设每一个结点可以包含 8 个键(当然真实情况下没有这么平均,有的结点包含的键可能比8多一些,有些比 8 少一些),那么整颗树的高度将最多 8 ( log8(838,8608)=7.8 ) 层,也就意味着磁盘查找一个叶子结点上的键的磁盘访问时间只有 8 次,这就是 B-树提出来的原因所在。
1.2、B树的特点
下面讲一下B树的特点
在讲B树的特点之前,我们先来了解几个概念
度:degree 指树中节点的孩子数
阶:order 指所有节点中孩子数最大值
B树的特点:
- 每个节点最多有m个孩子,其中m称为B-树的阶;(孩子数目的上限)
- 除根节点和叶子节点外,其他节点至少有 ceil(m/2) (阶数除以2向上取整)个孩子,就是说B树中节点最大有m个孩子即阶个孩子,至少有 m/2(向上取整) 个孩子;(孩子数目的下限)
- 若根节点不是叶子节点,则至少有两个孩子;(根节点孩子数的下限)
- 所有叶子节点都在同一层;(B树是否平衡的前提条件)
- 每个非叶子节点由 n 个关键字(就是n个关键值,参考二叉搜索树中的关键值)和 n+1 个指针(就是n+1个孩子)组成,其中 ceil(m/2)-1 <= n <= m-1;
- 关键字按非降序排列(就是升序排列,和二叉树搜索相同),即节点中的第 i 个关键字大于等于第 i-1 个关键字;
- 指针P[ i ] 指向关键字值位于第 i 个关键字和第 i+1 个关键字之间的子树;
这些特性都要理解。看一下一个B树的实例:
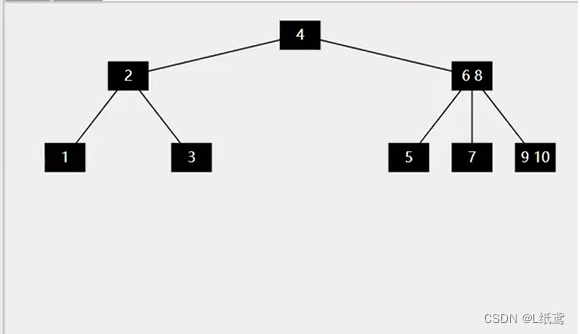
2.B树的节点类
下面,我们来看一下B树的具体实现吧
package Tree;import java.util.Arrays;public class L5_BTree {//B数的节点类static class Node{int[] keys; //关键字,即关键值,排序用的Node[] children; //孩子,存孩子用的节点类数组int keyNumber; //有效关键字数目(就是真正存了几个关键字)boolean leaf = true; //是否是叶子节点int t; //最小度数(最小孩子数)//构造函数public Node(int t) { // t >= 2this.t = t;//手动设置最小孩子数this.children = new Node[2 * t];//最大孩子数是最小孩子数的二倍this.keys = new int[2 * t -1];//关键字的最大数量 是 最大孩子数-1}@Overridepublic String toString() {return Arrays.toString(Arrays.copyOfRange(keys,0,keyNumber));}//多路查找,就是我给你一个关键值,你返回这个关键值对应的节点Node get(int key){int i = 0; //设置个变量i,方便用来循环遍历while (i < keyNumber){ //节点中有关键字if (keys[i] == key){ //如果节点中的关键字 等于 我给出的关键字,那就返回这个关键字对应的节点return this;}if (keys[i] > key){ //如果关键字中的最小值都比给出的大,那就直接退出这个节点的循环了break;}i++; //变量i自增}//执行到这里,就是说当前节点的关键字一定比给出的大,或者说,超出索引了,即keys[i]>key 或 i == keyNumberif (leaf){ //如果是叶子节点,那就肯定没有孩子了return null;}//这种情况就是 i == keyNumber 了,就找这个节点所对应的孩子了(孩子数比节点关键值数多1)return children[i].get(key);}//写一个方法,向 keys 指定索引 index 处插入 keyvoid insertKey(int key, int index){for (int i = keyNumber-1; i >= index ; i--) {keys[i+1] = keys[i];}keys[index] = key;keyNumber++;}//写一个方法,向 children 指定索引 index 处插入 childvoid insertChild(Node child, int index){System.arraycopy(children,index,children,index+1,keyNumber);children[index] = child;}//移除指定index处的keyint removeKey(int index){int t = keys[index];System.arraycopy(keys,index+1,keys,index,--keyNumber-index);return t;}//移除最左边的keyint removeLeftmostKey(){return removeKey(0);}//移除最右边的keyint removeRightmostKey(){return removeKey(keyNumber-1);}//移除指定index处的childNode removeChild(int index){Node node = children[index];children[index] = null;return children[index];}//移除最左边的childNode removeLeftmostChild(){return removeChild(0);}//移除最右边的childNode removeRightmostChild(){return removeChild(keyNumber);}//返回index孩子处左边的兄弟Node childLeftSibling(int index){return index > 0 ? children[index-1]:null;}//返回index孩子处右边的兄弟Node childRightSibling(int index){return index == keyNumber ? null : children[index+1];}//复制当前节点的所有key和child到targetvoid moveToTarget(Node target){int start = target.keyNumber;if (!leaf){for (int i = 0; i <= keyNumber; i++) {target.children[start+i] = children[i];}}for (int i = 0; i < keyNumber; i++) {target.keys[target.keyNumber++] = keys[i];}}}Node root; //定义一个根节点int t; //树中节点的最小度数(就是一个节点的最小孩子数,根节点叶子节点除外)final int MIN_KEY_NUMBER;//最小关键字的数量final int MAX_KEY_NUMBER;//最大关键字的数量//无参构造,最小度数默认值为2public L5_BTree() {this(2);}//有参构造public L5_BTree(int t) {this.t = t;root = new Node(t);//new出根节点,并给出根节点最小度数MIN_KEY_NUMBER = t-1;MAX_KEY_NUMBER = 2*t-1;}//判断关键字中是否存在指定关键字对应的节点public boolean contains(int key){return root.get(key) != null;}//新增一个关键字/**描述一下流程吧* 你构造一颗B树,给定了最小度数,那么最小关键字数、最大关键字数、阶数也就都定了* 你开始往节点中插入关键值,一开始没满,你继续插入* 当插入的关键字数等于最大关键字数时,这个节点就要分裂了,即将自身的关键字分出去,变为孩子节点* 然后你再插入,它就会按照关键字的顺序去选位置,* 如果找到位置了,是叶子节点,那么就直接插入(当然超过MAX_KEY_NUMBER就分裂一下)* 如果恰好发现一个非叶子节点里面也有位置,那么应该先搜索一下这个节点的孩子,然后再进行判断插在哪里* 当某个节点的关键字数再满,那这个树就再分裂一次* */public void put(int key){doPut(root,key,null,0);}//递归的函数private void doPut(Node node,int key,Node parent,int index){int i = 0;while (i < node.keyNumber){if (node.keys[i] == key){return; //更新逻辑}if (node.keys[i] > key){break; //找到插入位置,记为i}i++;}if (node.leaf){node.insertKey(key,i);//可能到达上限}else {doPut(node.children[i],key,node,i);//可能到达上限}if (node.keyNumber == MAX_KEY_NUMBER){split(node,parent,index);}}//分裂函数/*** left:要分裂的节点* parent:分裂节点的父节点* index:分裂节点是第几个孩子* */private void split(Node left, Node parent, int index){if (parent == null){//分裂的是根节点Node newRoot = new Node(t);newRoot.leaf = false;newRoot.insertChild(left,0);this.root = newRoot;parent = newRoot;}//1.创建right节点,把left中t之后的key和child移动过去Node right = new Node(t);right.leaf = left.leaf;System.arraycopy(left.keys,t,right.keys,0,t-1);//分裂节点是非叶子节点的情况if (!left.leaf){System.arraycopy(left.children,t,right.children,0,t);}right.keyNumber = t-1;left.keyNumber = t-1;//2.中间的key(t-1处)插入到父节点中int mid = left.keys[t-1];parent.insertKey(mid,index);//3.right节点作为父节点的孩子parent.insertChild(right,index+1);}//删除一个关键字public void remove(int key){doRemove(null,root,0,key);}private void doRemove(Node parent,Node node,int index,int key){int i = 0;while (i < node.keyNumber){if (node.keys[i] >= key){break;}i++;}//找到了,代表待删除key的索引//没找到,表示到第 i 个孩子里面继续查找if (node.leaf){if(!found(node, key, i)){//case1return;}else {//case2node.removeKey(i);}}else {if(!found(node, key, i)){//case3doRemove(node,node.children[i],i,key);}else {//case4Node s = node.children[i+1];while (!s.leaf){s = s.children[0];}int skey = s.keys[0];node.keys[i] = skey;doRemove(node,node.children[i+1],i+1,skey);}}if (node.keyNumber < MIN_KEY_NUMBER){//调整平衡 case5 and case6balance(parent,node,index);}}private void balance(Node parent, Node x, int i){//case6 根节点if (x == root){if (root.keyNumber == 0 && root.children[0] != null){root = root.children[0];}return;}Node left = parent.childLeftSibling(i);Node right = parent.childRightSibling(i);if (left != null && left.keyNumber > MAX_KEY_NUMBER){//case5-1 左边富裕 右旋//把父节点中前驱key旋转下来x.insertKey(parent.keys[i-1],0);if (!left.leaf){//left中最大的孩子换爹x.insertChild(left.removeRightmostChild(),0);}//left中最大的key旋转上去parent.keys[i-1] = left.removeRightmostKey();return;}if (right != null && right.keyNumber > MAX_KEY_NUMBER){//case5-2 右边富裕 左旋//把父节点中后继key旋转下来x.insertKey(parent.keys[i],x.keyNumber);//right中最小的孩子换爹if (!right.leaf){x.insertChild(right.removeLeftmostChild(),x.keyNumber+1);}//right中最小的key旋转上去parent.keys[i] = right.removeLeftmostKey();return;}//case5-3 两边都不富裕 向左合并if(left != null){//向左兄弟合并parent.removeChild(i);left.insertKey( parent.removeKey(i-1), left.keyNumber);x.moveToTarget(left);}else {//自己合并parent.removeChild(i+1);x.insertKey(parent.removeKey(i),x.keyNumber );right.moveToTarget(x);}}private boolean found(Node node, int key, int i) {return i < node.keyNumber && node.keys[i] == key;}}
为了对应代码中插入和删除的逻辑思路,下面给出两张图来看一下。
节点中插入key值后的节点分裂展示图:
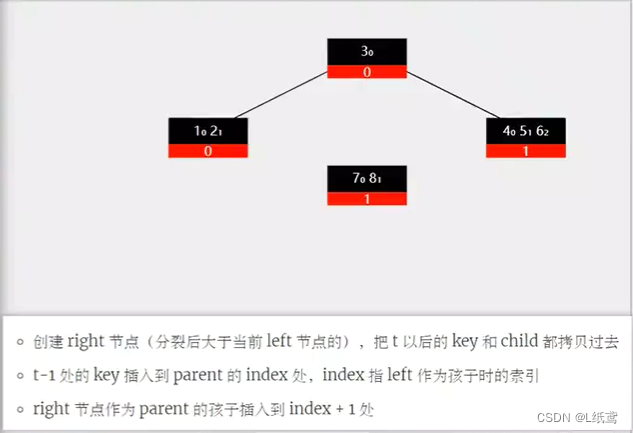
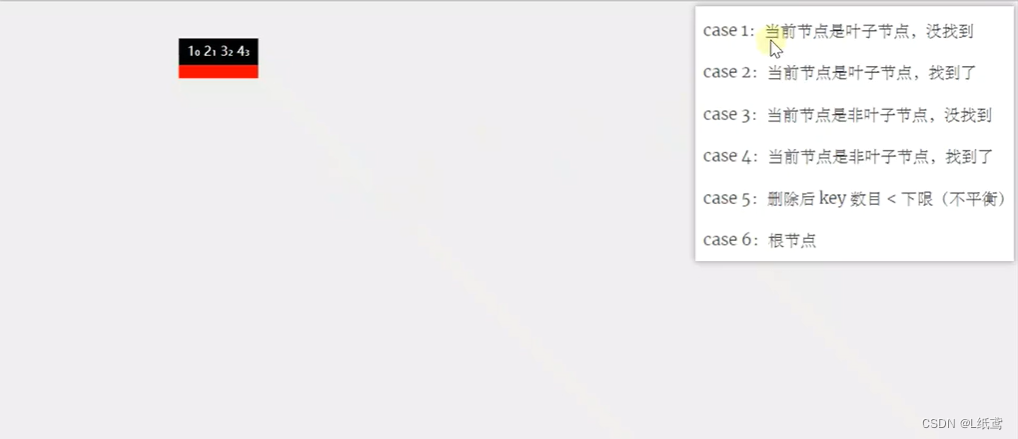
在节点中删除key的6种情况展示图(删除的是某个节点的key):
3.小结
说实话,我感觉这东西挺难的,写完之后脑瓜子都嗡嗡的。没有在纸上画图,单靠脑子想,我是肯定写不出来的,所以我的建议是:一定一定一定要画图,一定一定一定要看着图对着代码来一步一步的走,一定一定一定要看图!








![[每周一更]-第93期:探索大型生成式聊天工具:从ChatGPT到未来](http://pic.xiahunao.cn/[每周一更]-第93期:探索大型生成式聊天工具:从ChatGPT到未来)
![[前端][杂项] React版本](http://pic.xiahunao.cn/[前端][杂项] React版本)
的BMP280气压计驱动(I2C通信))






![[MAC] mac电脑更新 git的安装homebrew](http://pic.xiahunao.cn/[MAC] mac电脑更新 git的安装homebrew)
的行人检测器)
