漫步密度森林：借助HDBSCAN实现高效数据聚类

文章来源：navigating-the-density-forest-harnessing-hdbscan-for-advanced-data-clustering

2024 年 4 月 9 日

介绍

在数据科学中，聚类算法是揭示数据集内在结构的重要工具。在这些工具中，基于分层密度的噪声应用空间聚类 (HDBSCAN) 作为一种强大且通用的方法脱颖而出，用于发现不同形状和密度的聚类。本文深入研究了 HDBSCAN 的操作机制，阐明了其相对于传统聚类算法的优势，并讨论了其在实际场景中应用的实际考虑因素。

背景介绍

HDBSCAN (Hierarchical Density-Based Spatial Clustering of Applications with Noise) 是一种先进的聚类算法，它将 DBSCAN 转换为分层聚类算法，然后使用一种技术从分层树中提取平面聚类，从而扩展了 DBSCAN。以下是 HDBSCAN 的一些关键方面：

分层聚类： HDBSCAN 通过创建树枝图来建立聚类的层次结构，这使得聚类分配比 DBSCAN 更细致入微。
基于密度：与 DBSCAN 一样，HDBSCAN 也侧重于高密度区域，并试图将密度相似的区域连接成簇。它对噪声有很强的抗干扰能力，并能处理不同形状和大小的簇。
无需指定聚类数量：许多聚类算法需要事先指定聚类的数量，而 HDBSCAN 则不同，它会根据数据自动确定适当的聚类数量。
最小聚类大小： HDBSCAN 需要指定的主要参数是最小聚类大小，这有助于控制聚类的粒度。
处理噪声：HDBSCAN 能有效识别和排除噪声，将不适合任何聚类的数据点归入 "噪声 "类别。
应用：HDBSCAN 可用于异常检测、数据分析和生物信息学等多个领域，在这些领域中，了解未标记数据的固有分组情况至关重要。

HDBSCAN 在探索性数据分析中尤其有用，在这种分析中，数据结构是未知的，用户有兴趣识别数据集中的密集群组和异常值。

了解 HDBSCAN

HDBSCAN 的核心是将 DBSCAN 算法扩展到分层聚类框架中，增强其检测不同密度聚类的能力。该算法首先要构建一个 "互达距离 "图，作为构建连接组件层次结构的基础。这种层次结构以树枝图的形式表示，囊括了数据的密度聚类结构。

HDBSCAN 的一个显著特点是能够自动确定最佳聚类比例。为此，它将树状图转换成一棵浓缩树，树枝代表在不同密度阈值下持续存在的聚类。然后，该算法会根据聚类的持久性提取稳定的聚类，从而有效地识别出在不同尺度下仍保持高密度的群组。

与传统聚类方法相比的优势

HDBSCAN 具有多项优势，是许多从业人员的首选：

自动选择聚类：与 K-means 或标准 DBSCAN 不同，HDBSCAN 无需预先指定聚类的数量，而这在实际数据分析中往往是一个具有挑战性的决定。这一特点减轻了手动调整参数的负担，尤其是在探索性数据分析阶段。
处理噪声和异常值： HDBSCAN 能将噪声和异常值与重要数据点区分开来，从而提高所形成聚类的纯度。在异常检测等应用中，区分正常数据和异常数据至关重要，而这一特性尤其有益。
聚类形状的灵活性：该算法基于密度的方法使其能够识别任意形状和大小的聚类，与 K-means 等假定聚类为球形的方法相比，它更能适应复杂的数据结构。

实际考虑因素

要在实践中有效利用 HDBSCAN，数据从业人员需要考虑以下几个因素：

数据预处理：与许多聚类算法一样，HDBSCAN 的性能也会受到数据规模和性质的显著影响。对特征进行适当的规范化或标准化是确保算法准确捕捉底层数据结构的关键。
最小簇大小： HDBSCAN 的主要参数--最小聚类大小需要仔细选择。它决定了聚类的粒度，应根据具体情况和分析目标进行选择。
可解释性和验证：虽然 HDBSCAN 减少了对任意参数选择的需求，但解释由此产生的聚类并验证其与问题的相关性仍然至关重要。结合领域知识，利用剪影分数或其他验证指标，有助于评估聚类结果的质量和相关性。

代码

要说明在 Python 中使用 HDBSCAN 处理合成数据集的完整过程，包括特征工程、超参数调整、度量、绘图和解释，我们可以遵循以下步骤：

生成合成数据集。
执行特征工程
应用 HDBSCAN 聚类。
调整超参数
用指标进行评估。
结果可视化
解释结果。

以下是如何将这些功能整合到一个代码块中：

import seaborn as sns
import numpy as np
import pandas as pd
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler
import hdbscan
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score
# 1. Generate a synthetic dataset
X, _ = make_moons(n_samples=300, noise=0.1, random_state=42)
X = StandardScaler().fit_transform(X)  # Standardize for better clustering performance
# 2. Feature engineering (in this case, simple standardization)
X_standardized = StandardScaler().fit_transform(X)
# 3. Apply HDBSCAN clustering
clusterer = hdbscan.HDBSCAN(min_cluster_size=5, gen_min_span_tree=True)
labels = clusterer.fit_predict(X_standardized)
# 4. Hyperparameter tuning (skipping extensive tuning for brevity, but typically involves grid search or similar)
# 5. Evaluate with metrics
silhouette_avg = silhouette_score(X_standardized, labels)
print(f'Silhouette Score: {silhouette_avg:.2f}')
# 6. Visualize the results
plt.figure(figsize=(10, 8))
plt.scatter(X_standardized[:,0], X_standardized[:,1], c=labels, cmap='Spectral', s=50)
plt.title("HDBSCAN Clustering")
plt.colorbar(label='Cluster Label')
# Plot the cluster hierarchy
clusterer.condensed_tree_.plot(select_clusters=True,selection_palette=sns.color_palette('deep', 8))
# 7. Interpret the results
# Clusters are colored differently and noise points are typically colored in grey or black
# Silhouette score provides a metric for the cohesiveness of the clusters formed
print(f'Total clusters: {len(np.unique(labels)) - (1 if -1 in labels else 0)}')
print("Note: Negative label (-1) indicates noise points")

在这个例子中：

使用 sklearn 中的 make_moons 生成了一个合成数据集，该数据集创建了两个交错的半圆，这是聚类算法的一个典型测试案例。
在这种情况下，特征工程是最小的，因为我们处理的是一个简单的合成数据集，所以我们将特征标准化。
我们使用 HDBSCAN 对数据进行聚类，并将 min_cluster_size 作为主要的超参数。
我们可以使用网格搜索或贝叶斯优化等技术来找到超参数调整的最佳值，不过这里并没有广泛展示。
轮廓分数（silhouette_score）用于评估聚类性能，衡量一个对象与其聚类中其他对象的相似程度。
使用散点图对结果进行可视化，并通过浓缩树状图显示聚类层次，从而深入了解聚类的形成。
解释工作包括分析图和指标，以了解聚类结构和算法在捕捉数据固有分组方面的有效性。

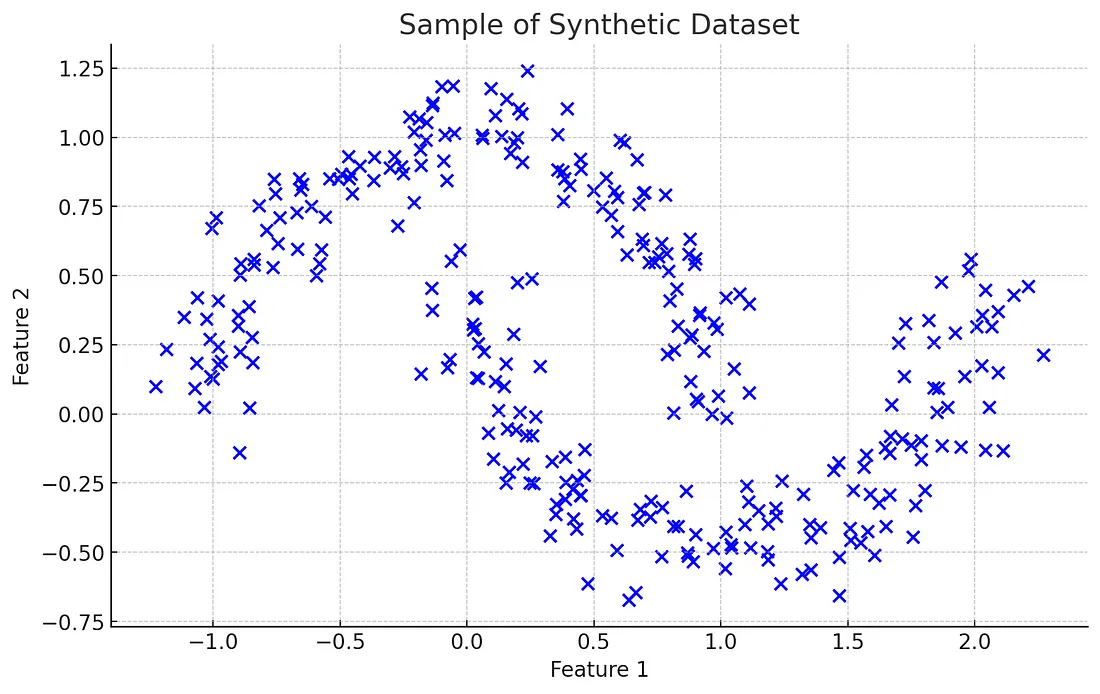
下面是使用 make_moons 函数生成的合成数据集的曲线图。这个数据集经常被用来演示聚类算法检测非线性模式的能力。它由两个交错的半圆组成，代表了一种传统线性聚类方法可能难以胜任，但 HDBSCAN 等算法却能大显身手的情况。

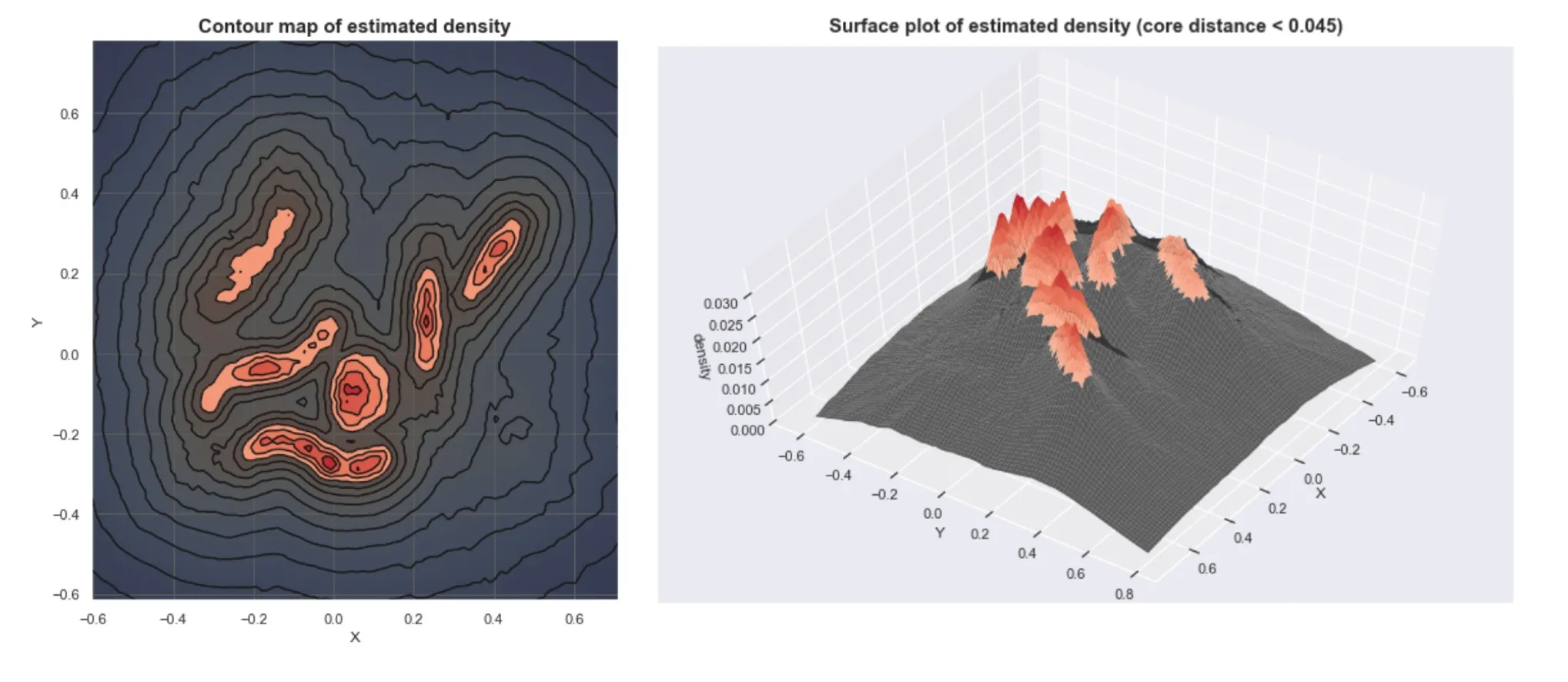
HDBSCAN 聚类算法生成了这幅浓缩树状图。以下是如何解释该图的各个部分：

y 轴上的 λ 值：这表示数据集中形成聚类的距离尺度。λ值越高，说明各点之间的距离越近，才能被视为同一聚类的一部分。随着 y 轴向下移动（λ 值越高），我们观察数据集的尺度就越小，因此，聚类将趋于合并。
树枝：每条垂直线代表给定 λ 值下的一个潜在聚类。当 λ 值增大时（即在图中向下移动时），横线会将合并的聚类连接起来。
λ=0时的彩条：颜色代表 HDBSCAN 识别出的不同聚类，每个彩条的长度与该聚类中的点数成正比。未包含在彩条内的点通常被视为噪声。
椭圆：它们通常突出显示特定的群集或感兴趣的点。它们表示在 λ 值范围内选定的稳定聚类，因此根据算法是可靠的。
右侧为颜色图例：这说明了颜色与群组标签之间的映射关系。左侧的条形图可能表示每个聚类在不同层次结构中的点数，颜色越深代表点数越多，颜色越浅代表点数越少。

在这幅图中，突出的黄色聚类表明在所选 λ 值临界点上有一个界限分明的大型聚类。在 λ=0 时，其他颜色的条形图显示有几个较小的群集，这表明数据集中有不同密度的密集区域（即有些密集，有些不那么密集）。

Silhouette Score: 0.23
Total clusters: 3
Note: Negative label (-1) indicates noise points

总之，这幅图显示了 HDBSCAN 发现的分层聚类结构，在不同的密度水平上发现了几个聚类，在较高λ 水平上可能存在大量噪声或连接不那么密集的点。

结论

HDBSCAN 是聚类分析领域的一大进步，为揭示复杂数据集中的潜在结构提供了灵活而强大的工具。通过自动确定聚类数量并有效处理噪声和异常值，从业人员可以将更多精力放在数据分析的解释性方面。然而，与任何分析方法一样，HDBSCAN 的成功应用也需要对其机制有细致入微的了解，对数据进行周到的预处理，并仔细考虑聚类参数。如果运用得当，HDBSCAN 可以揭示错综复杂的数据模式，有助于在从市场研究到生物信息学等各个领域做出有见地的决策。