IMU状态预积分的雅克比矩阵
- 预积分的雅克比矩阵
预积分的雅克比矩阵
最后讨论预积分相对状态变量的雅克比矩阵。由于预积分测量已经归纳了IMU在短时间内的读数,因此残差相对于状态变量的雅克比矩阵推导则简单。
首先考虑旋转。
旋转与Ri,Rj和 b g , i b_{g,i} bg,i有关,用SO(3)的右扰动来推导它:
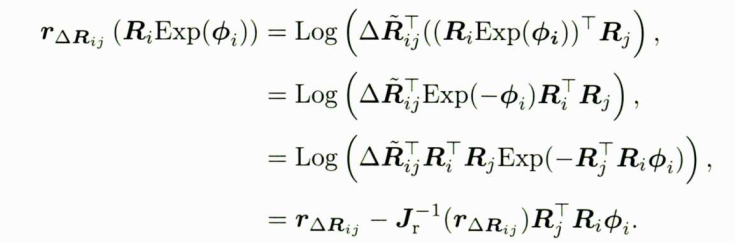
对 ϕ j \phi _{j} ϕj的导数为
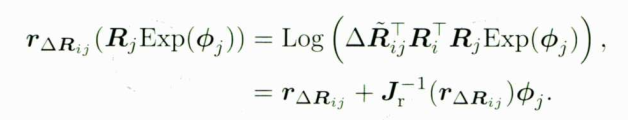
假设优化初始的零偏为 b g , i b_{g,i} bg,i,在某一步迭代时,当前估计出来的零偏修正为 δ b g , i \delta b_{g,i} δbg,i,而当前修正得到的预积分旋转观测量为
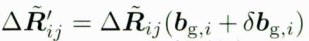
残差为 r △ R i j ′ r^{\prime }_{\bigtriangleup R_{ij}} r△Rij′
为了求导,又在上面两项的基础上加上了 δ ~ b g , i \tilde{\delta} b_{g,i} δ~bg,i,那么

所以最后得到
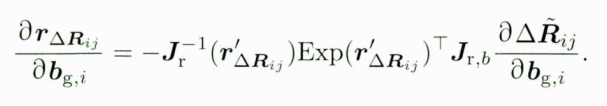
接下来,考虑速度项的雅克比矩阵。速度项与vi,vj呈线性关系,可以得到
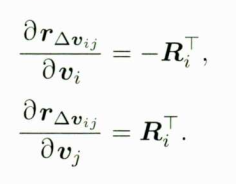
对旋转部分只需要做一阶泰勒展开:
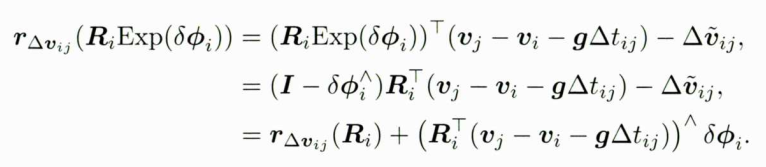
速度残差相对 b g , i , b a , i b_{g,i},b_{a,i} bg,i,ba,i的雅克比矩阵只和 △ v ~ i j \bigtriangleup \tilde{v} _{ij} △v~ij相关。由于速度的残差项与它只相差一个负号,所以只需要在下式中加个负号。
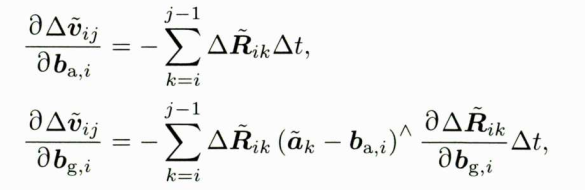
最后来看平移部分。平移部分和 p i , p j , v i , R i p_{i},p_{j},v_{i},R_{i} pi,pj,vi,Ri及两个零偏有关。然后,它们的关系大多为线性关系,雅克比矩阵可以得出
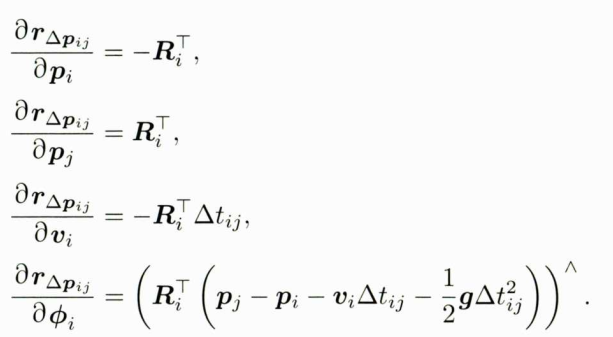
零偏的残差在下面基础上加负号
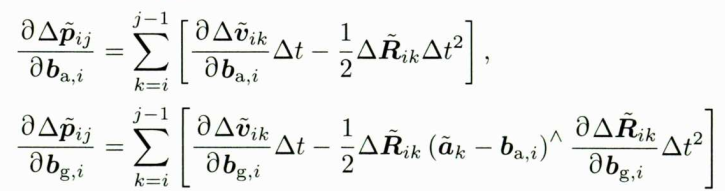






,chatglm3-6B 命名实体识别实战)

--CLIP笔记(一))

)
)
)






