目录
- 贪心算法
- 例题一:找零问题
- 例题二:走廊搬运物品最优方案问题输入样例
- 例题三:贪心自助餐
贪心算法
贪心算法是一种在每一步选择中都采取当前状态下最优的选择,以期望最终达到全局最优解的算法。它的核心思想是每次都选择当前最优解,而不考虑未来可能的情况。虽然贪心算法并不一定能够解决所有问题,但在一些特定情况下,它可以提供简单、高效的解决方案。
贪心算法适用于满足贪心选择性质和最优子结构性质的问题。贪心选择性质指的是每一步都选择当前最优解,而最优子结构性质指的是问题的最优解包含了子问题的最优解。
贪心算法的设计步骤通常包括:
- 确定问题的贪心选择性质: 需要明确每一步选择都是当前最优的特性。
- 构造解的候选集合: 根据贪心选择性质,确定每一步的选择范围。
- 确定选择的标准: 确定如何评价每个选择的优劣,并选择当前最优的解。
- 解决子问题: 通过递归或循环解决子问题。
- 合并子问题的解: 将各个子问题的解合并成原问题的解。
贪心算法是一种解决最优化问题的算法,其核心思想是在每一步选择中都采取当前状态下的最优选择,以期望最终达到全局最优解。相比之下,枚举法则是考虑所有可能情况,然后选出最优解。贪心算法与枚举法的不同之处在于贪心算法不进行回溯,而是在每个子问题中选择最优解后向下继续进行。
贪心算法主要适用于满足贪心选择性质的问题,即每一步选择都是局部最优解,最终得到的结果也是全局最优解的问题。贪心算法的设计步骤通常包括以下几个方面:
-
证明贪心选择性质: 证明问题的最优解可以通过一系列局部最优的选择得到。
-
将问题转化为贪心选择的形式: 将原问题转化为先做出选择,再解决剩下的子问题的形式。
-
求解子问题: 对每个子问题求解得到局部最优解。
-
合并子问题的解: 将子问题的局部最优解合并成原问题的解。
例题一:找零问题

输入:
在第一行给出测试例子个数 N ,用以代表需要找零的钱数
输入样例:
365
输出:
输出写法:
每一行输出数据输出找零的金额与数量
100:3
50:1
20:0
5:3
1:0
运行限制:
最大运行时间:1s
最大运行内存:128M
#include <iostream>
#include <algorithm>
#include<cstdio>
using namespace std;//面值
int t[5]={100, 50, 20, 5, 1};//张数
int m[5];void change(int n)
{for(int i=0;i<5;i++){m[i]=n/t[i];n=n%t[i];//print("%d",n);}
}int main()
{int N;cin>>N;change(N);for(int i=0;i<5;i++){printf("%d:%d\n",t[i],m[i]);}
}
例题二:走廊搬运物品最优方案问题输入样例
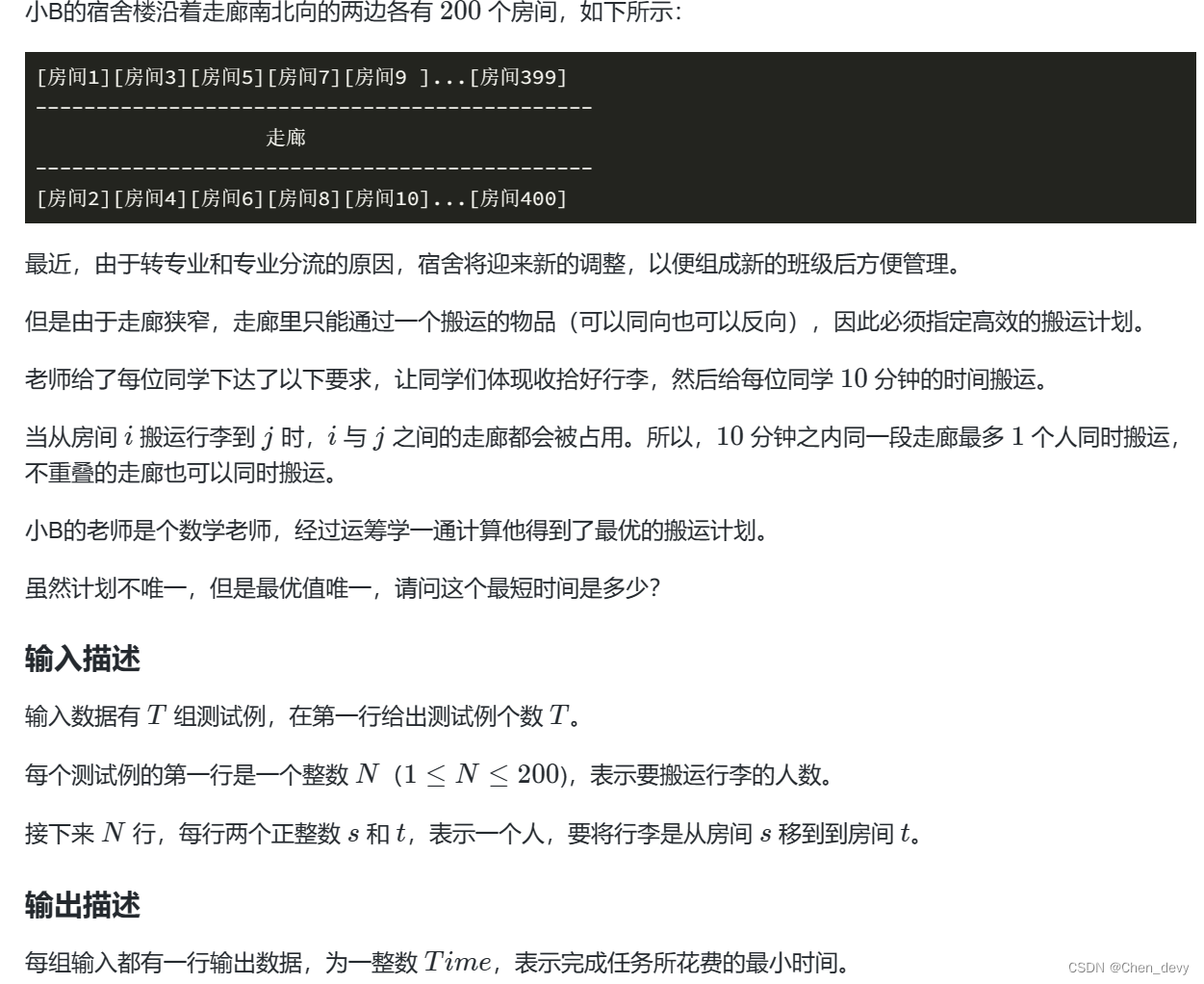
3
4
10 20
30 40
50 60
70 80
2
1 3
2 200
3
10 100
20 80
30 50
输出示例:
//每行代表每组完成任任务花费的最小时间
10
20
30
题目分析:
-
初步输入处理:
- 首先输入
T表示测试用例的数量。 - 然后循环处理每个测试用例,首先输入
N表示搬运次数,然后输入每次搬运的起点和终点。
- 首先输入
-
处理流程:
- 首先将起点和终点映射为走廊号,即通过
(房间号 - 1) / 2计算出走廊号。 - 确保起点比终点小,如果起点大于终点,则交换二者。
- 统计每个走廊被占用的次数,并同时更新最大占用次数
maxAns。 - 输出最大占用次数乘以 10,即为最短时间。
- 首先将起点和终点映射为走廊号,即通过
-
时间复杂度:该算法的时间复杂度主要取决于循环次数,即搬运次数
N。在每次搬运中,涉及到的操作都是常数时间的,因此总体时间复杂度为 O(N)。 -
空间复杂度:该算法的空间复杂度主要取决于
move数组,大小为 200。因此空间复杂度为 O(1)。
题解代码示例:
#include <cstdio>
#include <iostream>
#include<bits/stdc++.h>
using namespace std;/* - `move[200]`: 用于记录走廊的占用情况,数组下标表示走廊号,数组值表示该走廊被占用的次数。- `N`: 表示搬运次数,即每次搬运操作的数量。- `T`: 表示测试用例的数量。- `from`, `to`: 每次搬运的起点和终点。*/
int main()
{int move[200];
//搬运次数int N;int T;cin>>T;while(T--){//每次搬运的起点和终点int from, to;int maxAns=0;scanf("%d", &N);memset(move, 0, sizeof(move));for(int i = 0; i < N; i++){scanf("%d%d", &from, &to);
//将房间号映射为走廊号from = (from - 1)/2;to = (to - 1)/2;
//确保from<to,C++使用:swap(from, to)if(from > to)//确保起点比终点小{int temp = from;from = to;to = temp;}
//统计占用走廊情况,并统计最大值for(int j = from; j <= to; j++){move[j]++;maxAns=max(maxAns,move[j]);}}cout<<maxAns*10<<endl;}
}
例题三:贪心自助餐

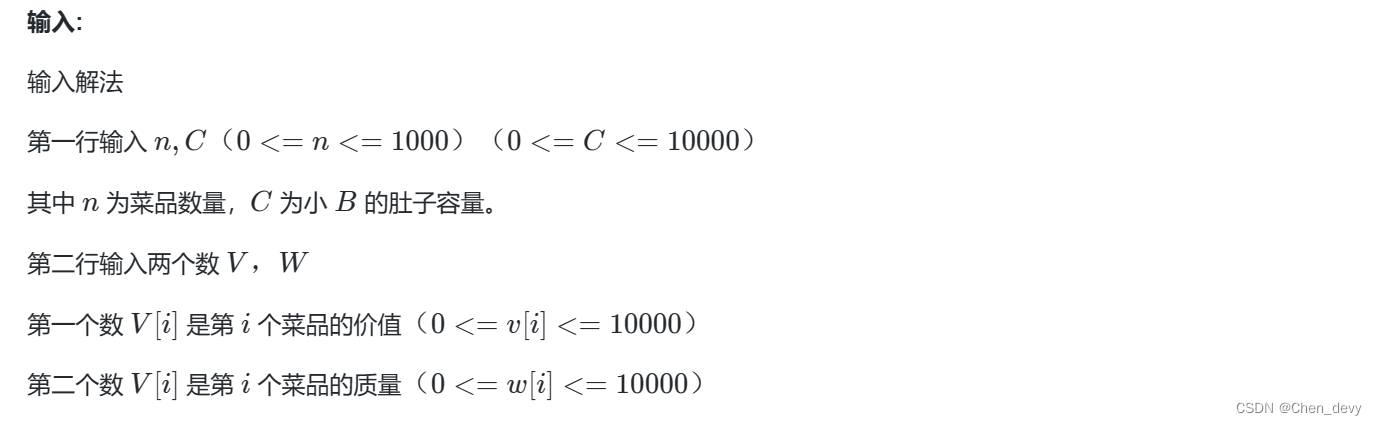
输入样例:
20 1000
1 22
2 43
123 214
12 2
123 432
21 223
22 16
77 49
34 78
34 9
43 677
21 34
23 23
12 56
332 56
21 99
123 545
389 33
12 999
23 88
输出;
输出一行数据,表示最大的价值,保留三位小数。
输入样例:
1204.114
题解代码示例:
#include <iostream>
#include <algorithm>
#include<iomanip>
using namespace std;//需要一个结构体,通过性价比,能够查找到重量和价值。//做一个排序,需要将性价比由高到底排序,排序的过程中重量和(价值)要对应上struct Food
{double w;double v;double aver;};
//C++一般用 struct,因为默认都是public的bool cmp(Food a, Food b)
{return a.aver > b.aver;//助记大于号就是从大到小排序,小于号就是从小到大排序
}int main()
{Food foods[1009];int n;double C;double Value = 0;cin >> n >> C;for (int i = 0; i < n; i++){cin >> foods[i].v>>foods[i].w;//求性价比foods[i].aver = foods[i].v / foods[i].w;//cout << foods[i].aver << endl;}//性价比排序sort(foods, foods + n, cmp);//当背包(肚子)能装下所有物品(菜)时,直接输出所有的物品(菜品)价值之和//int sum = 0;for (int i = 0; i < n; i++){sum += foods[i].w;}if (sum <= C){for (int j = 0; j < n; j++)Value += foods[j].v;//V = floor(V * 1000.0) / 1000.0;cout << setiosflags(ios::fixed) << setprecision(3) <<Value << endl;return 0;}//当背包(肚子)不能装下所有物品时应该由性价比的顺序,选择装入的物品for (int i = 0; i < n; i++){if (foods[i].w <= C){Value =Value + foods[i].v;C = C - foods[i].w;}else{//直接将剩余的C加入即可Value =Value + C * foods[i].aver;C = 0;}if (C == 0)break;}//V = floor(V * 1000.0) / 1000.0;cout << setiosflags(ios::fixed) << setprecision(3) <<Value << endl;return 0;
}感谢阅读!!!
【数据结构与算法】系列文章链接: 【数据结构与算法】递推法和递归法解题(递归递推算法典型例题)
【数据结构与算法】系列文章链接: 【数据结构与算法】C++的STL模板(迭代器iterator、容器vector、队列queue、集合set、映射map)以及算法例题
【数据结构与算法】系列文章链接: 【数据结构与算法】搜索算法(深度优先搜索 DFS和广度优先搜索 BFS)以及典型算法例题
【数据结构与算法】系列文章链接: 【数据结构与算法】二分查找算法


复现)




)


)





:Native层)


