LC 450.删除二叉搜索树中的节点

450.删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:

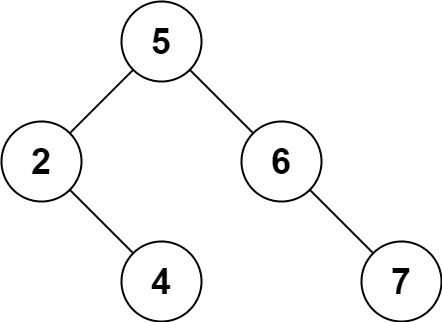
输入： root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释： 给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

节点数的范围 $0, 10^4]$ .
$-10^5 \leq Node.val \leq 10^5$
节点值唯一
root 是合法的二叉搜索树
$-10^5 \leq key \leq 10^5$

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

解法一(模拟+递归)

思路分析：

首先考虑二叉搜索树的特征，即左子树节点小于中间节点值，右子树节点大于中间节点值
因此对于找到需要删除的节点，即key与node.val进行比较
1. 如果key < node.val 则待删除节点在左子树
2. 如果key > node.val 则待删除节点在右子树
3. 如果key = node.val 则找到待删除节点，并执行删除逻辑
找到待删除节点后，需要根据二叉搜索树的定义执行删除，主要分为以下三种情况
1. 删除节点的左子树为空且右子树不为空或左子树不为空且右子树为空；则将不为空的子树连接到二叉搜索树中
2. 若删除节点的左右子树均为空，则直接删除该节点即可
3. 若删除节点的左右子树均不为空，则根据二叉搜索树的定义有左子树 < 右子树，即将左子树链接到右子树最左节点后，将右子树返回即可

实现代码如下：

class Solution {public TreeNode deleteNode(TreeNode root, int key) {return dfs(root, key);}private TreeNode dfs(TreeNode node, int key) {if (node == null)return null;	// 边界条件if (node.val > key) {node.left = dfs(node.left, key);		// 说明待删除节点在左子树 继续递归} else if (node.val < key) {node.right = dfs(node.right, key);	// 说明待删除节点在右子树 继续递归} else {	// 找到待删除节点if (node.left == null && node.right == null) {return null;} else if (node.left == null || node.right == null) {return node.left == null ? node.right : node.left;	// 返回不为null的子树} else {TreeNode pos = node.right;while (pos.left != null)pos = pos.left;pos.left = node.left;	// 将左子树链接到右子树最左端末尾return node.right;}}return node;}
}

提交结果如下：

解答成功:
执行耗时:0 ms,击败了100.00% 的Java用户
内存消耗:44.8 MB,击败了42.11% 的Java用户

复杂度分析：

时间复杂度： $O (h)$ ，h指二叉搜索树的高度
空间复杂度： $O (h)$

优化解法一(维持树的高度)

思路分析：

结合题解，对于以上解法一删除节点后，对左右子树的链接作优化，从而维持二叉搜索树在一定的高度
对于如何链接，即将右子树的最左端节点，即最小节点找出，然后将其作为新的左右子树的根节点，如此则可以避免直接将左子树链接到右子树最左端，导致二叉搜索树高度增加过大
同时因为将右子树最左端节点作新的根节点，也需要将右子树的最左端节点给删除，防止节点重复出现

实现代码如下：

class Solution {public TreeNode deleteNode(TreeNode root, int key) {return dfs(root, key);}private TreeNode dfs(TreeNode node, int key) {if (node == null)return null;	// 边界条件if (node.val > key) {node.left = dfs(node.left, key);		// 说明待删除节点在左子树 继续递归} else if (node.val < key) {node.right = dfs(node.right, key);	// 说明待删除节点在右子树 继续递归} else {	// 找到待删除节点if (node.left == null && node.right == null) {return null;} else if (node.left == null || node.right == null) {return node.left == null ? node.right : node.left;	// 返回不为null的子树} else {TreeNode pos = node.right;while (pos.left != null)	// 寻找右子树的最左端节点pos = pos.left;// 右子树的最左端节点作为新的根节点node.val = pos.val;		// 将pos节点值赋值给当前根节点 即pos作为新的根节点node.right = dfs(node.right, pos.val);	// 删除重复出现的pos节点值}}return node;}
}