1.粒子群算法PSO
博主言简意赅总结-算法思想:大方向下个体自学习探索+群体交流共享 对比适应度找到最优点
背景
粒子群优化算法(Particle Swarm Optimization,PSO)是一种启发式优化算法,通过模拟鸟群或鱼群等自然界中的群体行为来求解优化问题。
在PSO算法中,将待优化的问题看作一个多维空间中的搜索问题,将解空间中的每个候选解看作一个粒子,并将每个粒子的位置视为该解的可能解。每个粒子都有自身的位置和速度,同时根据自己的经验和群体的经验来调整自己的位置和速度,从而找到最优解。
PSO算法的基本思想是,通过不断地更新粒子的速度和位置来搜索解空间。每个粒子根据自身的经验和群体的经验来更新自己的速度和位置。具体而言,每个粒子根据当前的速度和位置以及自身历史最优位置和群体历史最优位置来计算新的速度和位置。通过不断地迭代更新,粒子群逐渐向全局最优解靠拢。
PSO算法相比于其他优化算法具有简单、易于实现和收敛速度快等特点,适用于解决连续优化问题和离散优化问题。在实际应用中,PSO算法已经被广泛应用于函数优化、机器学习、数据挖掘等领域,并取得了较好的效果。
基础知识
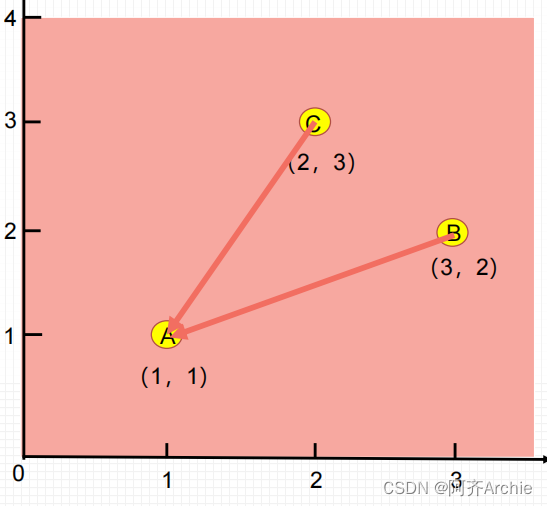
1.某个粒子(点)的移动,是有大小,有方向的。
2.有大小,有方向的东西叫向量。
算法原理
在前面基础知识章节举的例子是一个2维的空间,如果用群优化神经网络可能有上百上千个参数,就形成了D维。
假设在一个D维的目标搜索空间中,有N个粒子(种群大小)组成一个群落,其中第i个粒子表示为一个D维的向量,即位置:
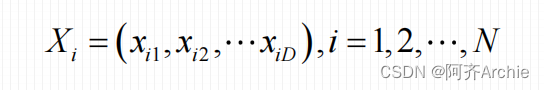
第i个粒子的“飞行”速度也是一个D维的向量(每个粒子有自己的方向),记为:
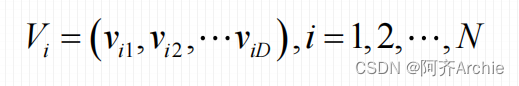
有全局最优方向,每个粒子也有自己的最优方向,类似于我们有自己的想法,你觉得自己的想法好,同时他人也在说自己的想法好,现在要做的就是你坚持自己的想法同时也考虑向他人想法好的地方的去学习,因此大家都这样子去齐心协力去做,对于全局来说肯定是好的。发现好的想法就进行一次更新迭代。
在第t次迭代的第i个粒子向第t+1次迭代进化时,根据如下式子更新位置:
每次迭代分析最佳位置,再次进行更新迭代,更新位置
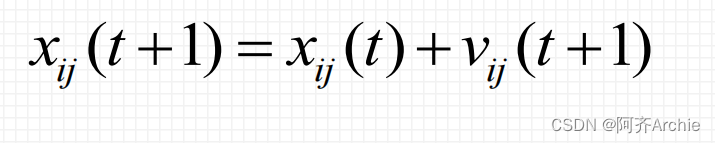
其中,Xij(t)加上更新的下一代方向Vij(t+1),实现t代xi的位置更新到t+1代xi的位置,更新位置。
其中,更新的下一代方向Vij(t+1)由以下三项组成:
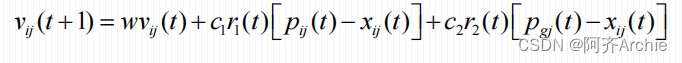
- 其中三项对应于: 惯性(自身)+ 局部方向 + 全局方向
- 第一项的Vij(t)为原本自身大小和方向
- 第二项的Pij(t)表示个体极值(个体最优位置),Pij(t)-Xij(t)表示向个体最优位置飞行的大小和方向
- 第三项的Pgj(t)表全局最值(全局最优位置),Pgj(t)-Xij(t)表向全局最优位置飞行的大小和方向
- 三个参数:参数w(惯性权重)和c1(个体学习系数)和c2(全局学习系数)
- r1(t)和r2(t)为随机数
以上就是PSO算法的原理,接下来举例理解以上过程:
如下图中,假设某粒子当前位置C,个体极值位置B,全局最优位置A,那么该粒子下一步的运动状态如图中蓝色线所示。图中B对应上式中的𝑝𝑖,A对应𝑝𝑔,黄色向量为当前速度方向,绿色向量为向个体极值飞行步长,红色为向全局最值飞行步长。
蓝色线(下一步方向)=红(全局最优方向)+黄(自身惯性(上一次飞行方向))+绿(个体找到的最优方向)
- 下一步方向是红、黄、绿三者的方向合成向量
- 若下一步到达c'不是优的地方还没有C好,就不更新C的位置为C',还保留原本的C位置,C位置不再动,其它的点进行更新

算法流程
输入 : 参数𝜔:一般0.5 − 0.8, 𝑐1, 𝑐2:一般0.1 − 2, 𝑣𝑚𝑎𝑥(指定搜索速度), 𝑥𝑚𝑎𝑥(指定搜索空间):取决于优化函数
Step1:初始化种群𝑥;
算法优缺点
2.量子粒子群算法QPSO
具有量子行为的PSO算法(QPSO)是在经典的粒子群算法(PSO算法)的基础上改进形成,它主要是结合了量子物理的思想修改了PSO的“进化”方法(即更新粒子位置的方法),在更新粒子位置时重点考虑各个粒子的当前局部最优位置信息和全局最优位置信息,具体方法见下面“具有量子行为的微粒群算法的运算过程”的描述。
QPSO 加入了量子力学的思想。在量子力学中,粒子可以同时处于多个状态,这就是量子叠加的概念。QPSO 引入了类似的概念,允许粒子同时处于多个位置。这样一来,搜索空间就会更加广阔,粒子们就有更大的机会找到最优解。
另外,QPSO 还考虑了量子干涉的概念。在量子力学中,粒子之间会相互干涉,影响彼此的运动轨迹。QPSO 中的粒子也会相互影响,这样可以增加搜索的多样性,防止陷入局部最优解。
运算过程
对标准的PSQ算法而言,算法收敛速度很快,但极易陷入局部最优。为了解决之一不足,2004年,孙俊[46]从量子力学角度出发提出了量子粒子群(QPSO)算法,QPSO算法的全局搜索能力要远远优于一般的PSO算法。QPSO算法与PSO算法是两种不同的运动方式,并不是在PSO算法的位置与速度更新公式上添加算子,因在理论上QPSO算法与PSO算法的复杂度是相当的。
在QPSO算法中,粒子被认为具有量子行为并参考了量子力学中量子的不确定性原理,故无法同时确定粒子的位置与速度的精确值。QPSO算法中粒子的更新是通过观测得到新个体,即给定一个概率去观测粒子,那么就会得到它得一个位置,对于每个粒子来说,会随机产生多个概率,利用蒙特卡罗思想进行观测,得到多个个体,然后选取个体最优,并依次评价其余个体,最终得到下代个体,如此进行搜索[47]。QPSO算法中粒子没有速度矢量,其位置迭代公式为:

基于平均最优位置的OPSO算法。对于QPSO,在迭代过程中通过个体极值与全局极值的相关信息进行下一步搜索,迭代未期,群体多样性会急剧恶化,个体容易陷入局部最优,故而孙俊等在算法中引入了平均最优位置(mean bestposition,mbest)。平均最优位置就是所有粒子个体最优位置的平均,其表达式为:

在QPSO中,粒子群按照下面的三个式移动位置,QPSO算法的进化方程式为::
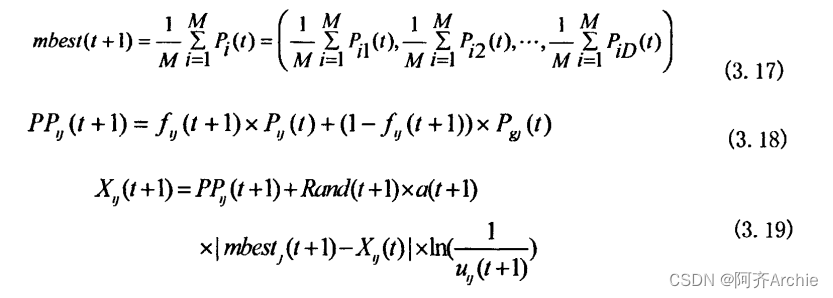

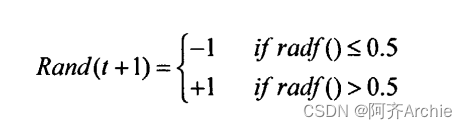


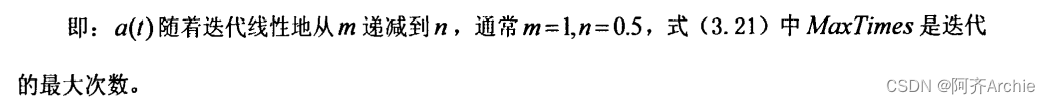

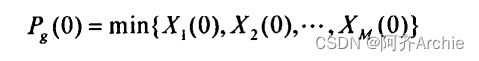

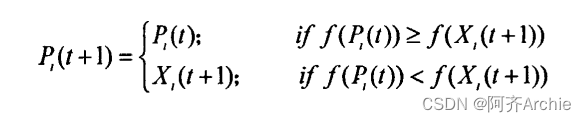


QPSO与PSO的比较












)
![[dvwa] sql injection(Blind)](http://pic.xiahunao.cn/[dvwa] sql injection(Blind))







