数理统计基础

统计学的基本概念

描述性统计学与推断性统计学

统计学可以划分为两个方面：描述性统计学与推断性统计学。描述性统计学主要是研究如何将数据各方面的重要特征通过不同统计量有效地、全面地进行总结。推断性统计学则是通过抽样样本的特征对研究对象总体进行预测、估计与判断。

总体与样本

区分总体与样本至关重要。总体是指研究对象的全体，而样本是指总体的子集¹。

四种度量尺度

若要选取恰当的统计方法对数据进行分析或描述，就必须了解度量数据不同的尺度。数据的度量尺度可以按照等级从弱到强，归为以下四种。

名义尺度

名义尺度就是通常所说的分类²。名义尺度是四种度量衡中等级最弱的一种，仅进行分类而不排序。

排序尺度

排序尺度是指根据数据的某些特征有次序的分类³。

区间尺度

相比于排序尺度，区间尺度进一步要求不同类别之间的差值是相等的⁴。然而，在区间尺度下，零点不具备数学上自然数0的意义⁵。因此，在区间尺度下，可以进行加减，但不能进行乘除。

比率尺度

比率尺度是等级最高的度量尺度。在比率尺度下，存在自然数意义上的零点，进行加减乘除也均有意义⁶。

度量尺度	特征
名义尺度	仅分类不排序，最弱的尺度
排序尺度	有次序的分类，只能比较不能加减
区间尺度	可以加减，但不能乘除，没有零点，如温度
比率尺度	有零点，可以加减乘除，等级最高

数据的展现

频率分布

数据整理是进行统计分析的第一步。最常见的整理数据方法就是绘制频率分布表。

直方图与频数多边形

除表格形式外，在很多情况下用图形展示数据会更加直观。

1. 直方图
   频数分布中最常用的图形展示就是直方图。直方图中的长条矩形宽度相等，表示组间距离，而长条矩形的高度即表示数据在区间内频数的高低。

2. 频数多边形
   频数多边形在直方图的基础上进行了改进，用折线图而不是柱状图的形式来绘制频数，频数多边形将直方图中每个区间的中点与频数对应，绘制相应散点图。

相比直方图，频数多边形更加连续，在分组区间个数较多时更加直观。相应地，还可以绘制累积频数分布图。

除了频数分布，数据集里还包含了各方面的信息，接下来将构造不同统计量以反映数据集不同方面的特征信息，包括中心趋势、离散程度、偏度与峰度四个维度。

中心趋势

中心趋势主要衡量数据汇集位置，可以从均值、中位数与众数三个指标进行度量。

均值

算术平均

算术平均是最常见的均值计算方法，其定义非常直观，即将所有数据加总后除以数据的个数。总体均值与样本均值的公式分别如下：
$$\mu =\frac{\sum _{i=1}^N{X}_i}{N}$$
$$\bar{X}=\frac{\sum _{i=1}^n{X}_i}{n}$$
算术平均的优点在于易于理解且利用了数据中所有数据信息；其缺点在于容易受极端值影响⁷。

几何平均

算数平均不适用于衡量多期的资产平均收益。

几何平均为n个数据相乘后开n次方，其计算公式如下：
$$G=\sqrt[n]{X_1{X}_2...X_n}$$
$$(X_i⩾0,i=1,2,3,...,n)$$
然而，当计算多期平均收益率时，应稍作修改如下：
$$Periodicretur{n}_{compound}=\sqrt[n]{(1+R_1)(1+R_2)...(1+Rn)}-1$$
其中，R_n代表第n期的收益率。

调和平均数

调和平均数是指观测值倒数平均值的倒数⁸，公式为：
$${\bar{X}}_{Harmonic}=\frac{n}{\sum _{i=1}^n\frac{1}{X_i}}$$

算术平均数、几何平均数与调和平均数之间的大小关系如下：
$$调和平均数⩾几何平均数⩾算术平均数$$
上述不等式的等号当且仅当X₁=X₂=…=X_n时成立。

加权平均

加权平均的概念在现代资产组合管理理论中被广泛使用⁹。

一般地，如果资产组合中有n个资产，则加权平均公式为：
$${\bar{X}}_W=\sum _{i=1}^n{w}_i{R}_i=w_1{R}_1+w_2{R}_2+...+w_n{R}_n$$
其中，w₁+w₂+…+w_n=1；w_i即为资产i的配置占比；R_i为资产i的收益率。不难发现，算术平均实际上是加权平均当w_i=1/n时的特例。

中位数

中位数是指一组升序或降序排列的数据中位于中间位置的数。假定共有n个数据，已按升序或降序排练。当n为奇数时，则中位数为处于（n+1）/2位置的数；当n为偶数时，则中位数为处于n/2与（n+2）/2两个位置上的数的平均值¹⁰。

中位数与算术平均值一样都是反映随机变量位置的特征值。然而，在数据中存在极端值的情况下，由于中位数只考虑位于中间位置的数，而不考虑极端值的大小，因此中位数比算数平均值更能反映数据特征。同样的，中位数的缺点在于，只利用了位于中间处的数据而忽视了数据中其他数据提供的信息。

众数

顾名思义，众数是指数据中出现频率最高的数¹¹。

关于众数，有几个特点需要留意。

1. 众数可以不止一个，只有一个众数的数据分布称为单峰，存在两个众数的数据分布称为双峰，三个众数称为三峰；
2. 如果数据中所有数据都不相等，则这个数据集不存在众数；
3. 当数据集是用名义尺度度量时，利用众数可以非常有效地识别出发生频率最高的类别。

离散程度

仅仅了解数据的中心位置是远远不够的。正如在进行投资时，只关注资产平均收益率而忽视资产本身风险，就有可能遭受灾难性的后果。“天下没有免费的午餐”，高收益必然伴随着高风险。基金经理在评估某一资产时，既要关注该资产的平均收益，也要衡量该资产的风险，即资产偏离平均收益率的程度，简称为离散程度。

绝对离散程度

分位数

全面了解数据分布状况不仅要确定中心位置，还要了解各个位置上的数据分布状况，这就要借助分位数的概念。分位数是指位于数据中指定位置的数据。中位数实际上就是一个特殊的分位数，即将数据集排序后等分为两个部分，中位数就是落在等分点位置的数据。类似地，相关概念可以拓展至四分位数、五分位数、十分位数与百分位数。例如，四分位数指将数据集排序后等分为4个部分，一共3个四分位数。在数据中，小于第1个四分位数的数据占比25%，小于第2个四分位数的数据占比50%，小于第3个四分位数的数据占比75%。同理，可定义五分位数、十分位数与百分位数。

然而，实际处理数据时，往往不会恰好有数据落在指定的位置。例如，定义中位数时，当数据个数为偶数时，数据中没有数据落在正中间的位置，于是就直接定义最中间两个数据的均值为中位数。可以利用以下公式确定分位数的位置。
$$L_y=(n+1)\frac{y}{100}$$
其中，n表示数据个数；y表示百分位点；L_y表示分位数的位置。

极差

极差是指数据中最大值与最小值之差：
$$极差=最大值-最小值$$
极差是了解数据集离散程度最简单的指标，其缺点在于仅确定了数据集的上下界，而不知道数据的具体离散程度。

平均绝对离差

度量数据集的离散程度最直观的想法就是考察数据集中每一个数据偏离均值的程度，即$X_i-\bar{X}$。然而，直接将所有$X_i-\bar{X}$加总是等于0的。这是因为数据$X_i$必然是环绕分布在$\bar{X}$上下的，加总后正负抵消就为0[由于$\bar{X}=\sum X_i/n$，故$\sum (X_i-\bar{X})=0$]。因此必须将取负值的$X_i-\bar{X}$转换为正数，转换为正数的一个方法就是取绝对值。

平均绝对离差是将数据集中每一个数据偏离均值的距离绝对值取算术平均，以反应数据集的离散程度。样本平均绝对离差的计算公式如下。
$$MAD=\frac{\sum _{i=1}^n|X_i-\bar{X}|}{n}$$
虽然平均绝对离差可以刻画出数据集的离散程度，但绝对值本身在数学上不是很好处理，不是处处可导的函数，不便于进一步深入研究其他问题。

方差与标准差

处理负值$X_i-\bar{X}$的另一种方法是取平方，从而引入“方差”的概念。总体方差指数据与总体均值间距离平方的算术平均值。类似地，可得样本方差公式。
$${\sigma }^2=\frac{\sum _{i=1}^N(X_i-\mu {)}^2}{N}$$
$$s^2=\frac{\sum _{i=1}^n(X_i-\bar{X}{)}^2}{n-1}$$
总体方差与样本方差开平方根后即可得总体标准差与样本标准差的公式：
$$\sigma =\sqrt{\frac{\sum _{i=1}^N(X_i-\mu {)}^2}{N}}$$
$$s=\sqrt{\frac{\sum _{i=1}^n(X_i-\bar{X}{)}^2}{n-1}}$$
方差与标准差均反映了数据的离散程度，两者的区别主要体现在量纲上。由于标准差的量纲与期望均值的量纲相同，更便于理解¹²。

相对离散程度

绝对离散程度在比较两个以上随机变量之间的波动程度时会存在问题。第一，不同随机变量的量纲可能不同，比如身高的标准差与收入的标准差基本单位不同，两者不具备可比性；第二，即便两个随机变量量纲相同，但取值大小可能相差很大，以至于标准差等离散指标不可比¹³。

变异系数（CV）

变异系数剔除了量纲以及取值大小的影响。变异系数定义为样本的标准差除以样本均值，其公式如下：
$$CV=\frac{s}{\bar{X}}$$

切比雪夫不等式

切比雪夫不等式以标准差为衡量单位，给出了任意数据集离散程度的上界：对任意一个方差<+∞的数据集来说，其数据在均值k个标准差范围内的占比至少为1-1/k²，其中k＞1.

偏度与峰度

偏度

仅靠均值和方差还不足以全面衡量投资收益率的分布。这就要引入偏度的概念，以反映数据分布的对称性。样本偏度公式如下：
$$Sampleskewness(S_k)=[\frac{n}{(n-1)(n-2)}]\frac{\sum _{i=1}^n(X_i-\bar{X}{)}^3}{s^3}$$
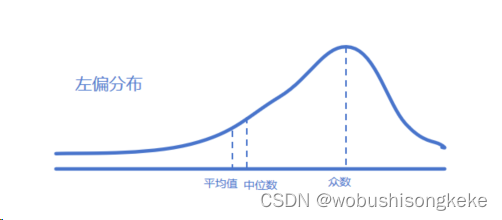
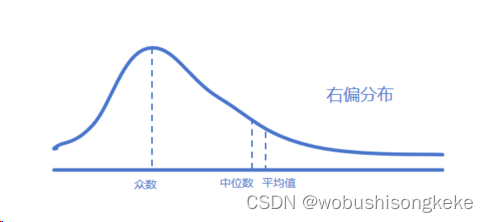
当偏度大于0时，说明相对而言X_i右向偏离$\bar{X}$的值较多，数据分布呈现出右偏，也称正偏；当偏度小于0时，说明相对而言X_i左向偏离$\bar{X}$的值较多，数据分布呈现出左偏，也称负偏。

有关偏度的另一重要考点就是判断左偏或右偏时，均值、中位数与众数的相对大小。左偏时，分布的均值＜中位数＜众数；右偏时，分布的众数＜中位数＜均值。

峰度

偏度衡量是尾部的长度，即更长的尾部是偏向左边还是右边，峰度则进一步衡量尾部的厚度。样本峰度的公式如下：
$$Samplekurtosis(K)=[\frac{n(n+1)}{(n-1)(n-2)(n-3)}]\frac{\sum _{i=1}^n(X_i-\bar{X}{)}^4}{s^4}$$
同偏度一样，峰度的公式无需记忆，只需了解样本峰度是有关$\sum _{i=1}^n(X_i-\bar{X}{)}^4$的表达式，衡量尾部厚度。峰度值高说明$X_i$偏离$\bar{X}$的极端值较多，尾部较厚；反之，峰度值低说明$X_i$偏离$\bar{X}$的极端值较少，尾部较薄。实际运用中，通常将正态分布的峰度作为基准，正态分布的峰度为3。若峰度高于3，则称为尖峰态，图形上比正态分布呈现出尖峰肥尾；若峰度低于3，则称平峰态，图形上相比于正态分布呈现出矮峰瘦尾。

此外，由于进行比较时通常习惯于以0为基准，于是定义超峰度=峰度-3。正态分布的超峰度为0，称为常峰态。尖峰态的超峰度大于0，平峰态的超峰度小于0.

	Leptokutic	Mesokutic	Platykutic
样本峰度	＞3	=3	＜3
超峰度	＞0	=0	＜0

---

1. 例如，考察中国人的收入状况。假定全中国共有N个人，抽样调查n个人的收入状况。那么，所有中国人的收入就是总体，即集合{x₁,x₂,…,x_N}，其中x_i表示第i个人的收入，而抽样调查n个中国人的收入就是样本（n<N），即集合{x₁,x₂,…,x_n}。 ↩︎

2. 例如，将股票分为价值型与成长型两类，用数字1代表某个股票属于价值型，数字2代表某个股票属于成长型。这里的数字1与数字2仅代表股票所属的种类，数字本身没有大小之分。 ↩︎

3. 例如，某基金公司将其所有基金经理分为三个级别，数字3代表最高级别、历史业绩最好的高级基金经理，数字1代表低级别、历史业绩最差的初级基金经理。与名义尺度不同，这里的数字具有排序上的意义，级别3的基金经理历史业绩好于级别2的基金经理。但需要注意的是，排序尺度只能进行比较，不能进行加减。换言之，我们仅仅知道级别3基金经理的业绩优于级别2的基金经理，但两者具体差距多少是无法得知的，且级别3与级别2基金经理业绩上的差距不一定等于级别2与级别1之间的差距。 ↩︎

4. 区间尺度最常见的例子就是温度。10℃与11℃之间的温差是等于24℃与25℃之间的温差的。因此，在区间尺度下，进行加减是有意义，例如15℃+10℃=25℃。 ↩︎

5. 例如0℃代表了某个温度的具体级别，但不表示没有任何温度。 ↩︎

6. 许多常见的指标都是比率尺度，如身高、收入、资产收益率（均有自然数意义上的零点，收入为0就代表没有任何收入）。 ↩︎

7. 例如计算5只股票的平均年化收益率，假定其中4只股票年化收益率均为0，剩余1只为100%。若单看算术平均值20%，是一个收益率不错的组合，但实际上这个算术平均值受到极端值100%的影响较大，多数股票年化收益率仅为0%。 ↩︎

8. 调和平均数主要被运用于计算“定投”的平均成本。 ↩︎

9. 例如，一个资产管理规模为100亿的基金，其中40亿资金配置债券，60亿配置股票。假定债券年化收益率为10%，股票年化收益率为20%，那么应该如何计算该基金资产组合的年化收益率呢？这就涉及如何对债券与股票收益率平均。直接计算算术平均值显然是不合理的，因为两者的配置比重不同。一个自然的想法就是以配置资金占比为权重，计算加权平均收益率=60/10020%+40/10010%=16%。 ↩︎

10. 例如，对于{2,5,7,11,14}这组数据，由于数据总数为奇数，故处于第（5+1）/2=3位的数，即位于正中间的数据7为中位数。又如，对于{3,7,9,10,15,20}这组数据来说，由于数据总数为偶数，因此位于正中间的数有两个，即9和10，中位数即为两者的平均值：（9+10）/2=9.5。 ↩︎

11. 例如，数据{2,4,5,5,7,8,8,8,10,12}中8出现次数最多，故众数为8。 ↩︎

12. 例如，假定某证券公司人均年薪20万元，方差为25万²，标准差5万元。显然，相比方差的单位万²，标准差的5万元更便于直观理解。 ↩︎

13. 例如，股市中，股票A的股价在600元上下波动，而股票B的股交在3元上下波动。两者的单位相同，均为元，股票A股价的标准差一定是大于股票B的，但这无法说明股票A的股价波动就一定高于股票B，因为两者的基准价相差甚远。因此，引入相对离散程度的概念，用于比较不同随机变量之间的离散程度。 ↩︎