[23年蓝桥杯H题] 合并石子

问题描述

在桌面从左至右横向摆放着 N 堆石子。每一堆石子都有着相同的颜色，颜色可能是颜色 0 ，颜色 1 或者颜色 2 中的其中一种。现在要对石子进行合并，规定每次只能选择位置相邻并且颜色相同的两堆石子进行合并。合并后新堆的相对位置保持不变，新堆的石子数目为所选择的两堆石子数目之和，并且新堆石子的颜色也会发生循环式的变化。具体来说：两堆颜色 0 的石子合并后的石子堆为颜色 1 ，两堆颜色 1 的石子合并后的石子堆为颜色 2 ，两堆颜色 2 的石子合并后的石子堆为颜色 0 。本次合并的花费为所选择的两堆石子的数目之和。给出 N 堆石子以及他们的初始颜色，请问最少可以将它们合并为多少堆石子？如果有多种答案，选择其中合并总花费最小的一种，合并总花费指的是在所有的合并操作中产生的合并花费的总和。
【输入格式】
第一行一个正整数 N 表示石子堆数。
第二行包含 N 个用空格分隔的正整数，表示从左至右每一堆石子的数目。
第三行包含 N 个值为 0 或 1 或 2 的整数表示每堆石头的颜色。
【输出格式】
一行包含两个整数，用空格分隔。其中第一个整数表示合并后数目最少的
石头堆数，第二个整数表示对应的最小花费。
【样例输入】

5
5 10 1 8 6
1 1 0 2 2

【样例输出】

2 44

【样例说明】
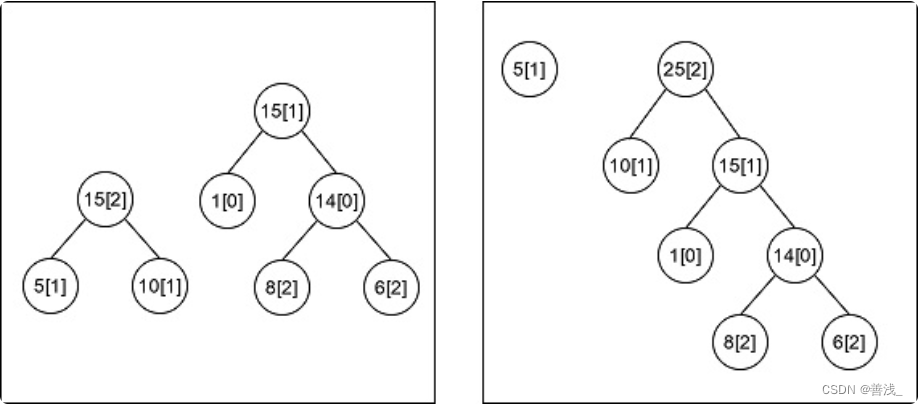
在这里插入图片描述
上图显示了两种不同的合并方式。其中节点中标明了每一堆的石子数目，
在方括号中标注了当前堆石子的颜色属性。左图的这种合并方式最终剩下了两
堆石子，所产生的合并总花费为 15 + 14 + 15 = 44 ；右图的这种合并方式最终
也剩下了两堆石子，但产生的合并总花费为 14 + 15 + 25 = 54 。综上所述，我
们选择合并花费为 44 的这种方式作为答案。
【评测用例规模与约定】
对于 30 % 的评测用例， 1 ≤ N ≤ 10 。
对于 50 % 的评测用例， 1 ≤ N ≤ 50 。
对于 100 % 的评测用例， 1 ≤ N ≤ 300 , 1 ≤ 每堆石子的数目 ≤ 1000 。

思路

推荐先学习没有颜色限制的手动模拟石子合并讲透区间动态规划参考闫氏分析法_哔哩哔哩_bilibili

dp设计

dp的思想是, 用二维dp保存区间的最小花费, 因为合并是两个两个区间一合并的, 所以一个区间的状态是由两个子区间转移过来的 , 这两个子区间不固定 , 所以要遍历来找和最小的 , 而两个子区间又有它们的子区间, 如此dp的思想便体现出来了

加入了颜色限制, 需要在原来的dp表上在加入一维表示颜色 dp[i][j][c] 表示在区间( i , j )合颜色为c的一个整堆需要的最小花费; 初始值为Integer.MAX_VALUE 表示在区间 i , j 内不能合并成该颜色的一个整堆
因为有颜色限制 , 两个子区间不一定是合并的 , 所以还要一个 dp 表 healCount 来保存最小堆数
因为区间不一定是合并的, 所以还还需要一个 cost 表来保存最小花费

状态转移方程

怎么判断计算 dp[i][j][c] 的值呢?
学习过没有颜色限制的我们会知道 , dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k + 1][j] + sum[j] - sum[j - 1]);
现在加入了颜色限制 , 也就是不所有dp[i][k] 都有效, 这个 (i , k)区间必须能合并成一个颜色c的整块, 所以先遍历颜色看再在遍历k的时候, 要测试颜色为c 的 (i , k) 区间和 (k + 1 , j) 区间是否都有效 , 都有效就尝试为dp[i][j][(c + 1) % 3] 赋值,

状态转移方程如下:

dp[i][j][(c + 1) % 3] = Math.min(dp[i][j][c], dp[i][k][c] + dp[k + 1][j][c] + sum[j] - sum[j - 1]);

对于最小堆数如果能合并成一个整堆 , 那么(i , j) 区间的最小堆数就是1 , 如果不能就遍历k , 分两个区间 , 到healCount表中去找最小的堆数

对于最小花费 , 如果能合并那么最小花费就是3种颜色种最小的一个; 不能合并就在堆数最小的情况中 , 找所有堆花费和的最小值

贴个代码

import java.util.Scanner;  /**  * @author Fancier  * @version 1.0  * @description: combineStones  * @date 2024/4/10 13:55  */  
public class Main {  public static void main(String[] args) {  new Solution();  }  
}  class Solution {  Scanner cin = new Scanner(System.in);  int n;  int[] sum;//石头总数的前缀和  int[][][] dp;//带有 颜色 的 i j 区间 的最小费用  int[][] healCount;//区间 i, j 最小堆数  int[][] cost;//区间 i ,j 最小石头数 public Solution() {  init();  for(int len = 1; len < n; len++) {  for (int i = 1; i + len <= n; i++) {  int j = i + len;  for (int c = 0; c < 3; c++) {  int temp = Integer.MAX_VALUE;  for(int k = i; k < j; k++) { //k 不能等于j 否则下面的k + 1就要大于j了  //在 i, j 区间内找颜色相同的两个堆  if (dp[i][k][c] != Integer.MAX_VALUE && dp[k + 1][j][c] != Integer.MAX_VALUE) {  temp = Math.min(temp, dp[i][k][c] + dp[k + 1][j][c] + sum[j] - sum[i - 1]);//如果能合并那么最后一次合并的花费就是所有的石子数  }  }  if (temp != Integer.MAX_VALUE) {  //如果符合条件 那么该区间就合成了一堆了  healCount[i][j] = 1;  //合并后颜色会改变  dp[i][j][(c + 1) % 3] = Math.min(dp[i][j][(c + 1) % 3], temp); }  }  cost[i][j] = Math.min(dp[i][j][0], Math.min(dp[i][j][1], dp[i][j][2])); for (int k = i; k < j; k++) {  if (healCount[i][j] > healCount[i][k] + healCount[k + 1][j]) {  healCount[i][j] = healCount[i][k] + healCount[k + 1][j];  //在堆数最小的情况下才会有符合条件的最小石头数  cost[i][j] = cost[i][k] + cost[k + 1][j];  } else if (healCount[i][j] == healCount[i][k] + healCount[k + 1][j]) {  cost[i][j] = Math.min(cost[i][j], cost[i][k] + cost[k + 1][j]);  }  }  }  }  System.out.println(healCount[1][n] + " " + cost[1][n]);  }  //初始化  private void init() {  n = cin.nextInt();  sum = new int[n + 1];  dp = new int[n + 1][n + 1][3];  healCount = new int[n + 1][n + 1];  cost = new int[n + 1][n + 1];  //初始化dp表  for (int i = 1; i <= n; i++) {  sum[i] = sum[i - 1] + cin.nextInt();  for (int j = 1; j <= n; j++) {  healCount[i][j] = j - i + 1;  if(i != j) cost[i][j] = Integer.MAX_VALUE;  for (int k = 0; k < 3; k++)  dp[i][j][k] = Integer.MAX_VALUE;  }  }  for (int i = 1; i <= n; i++)  //为什么初始化为零, 因为并就是一堆石头不许要花费  dp[i][i][cin.nextInt()] = 0;  }  
}