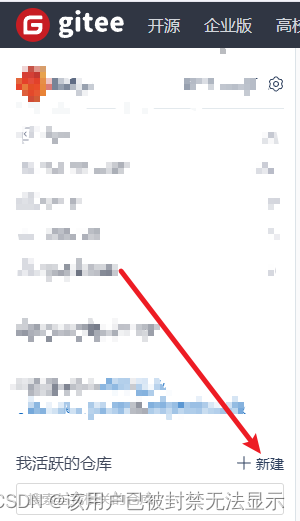
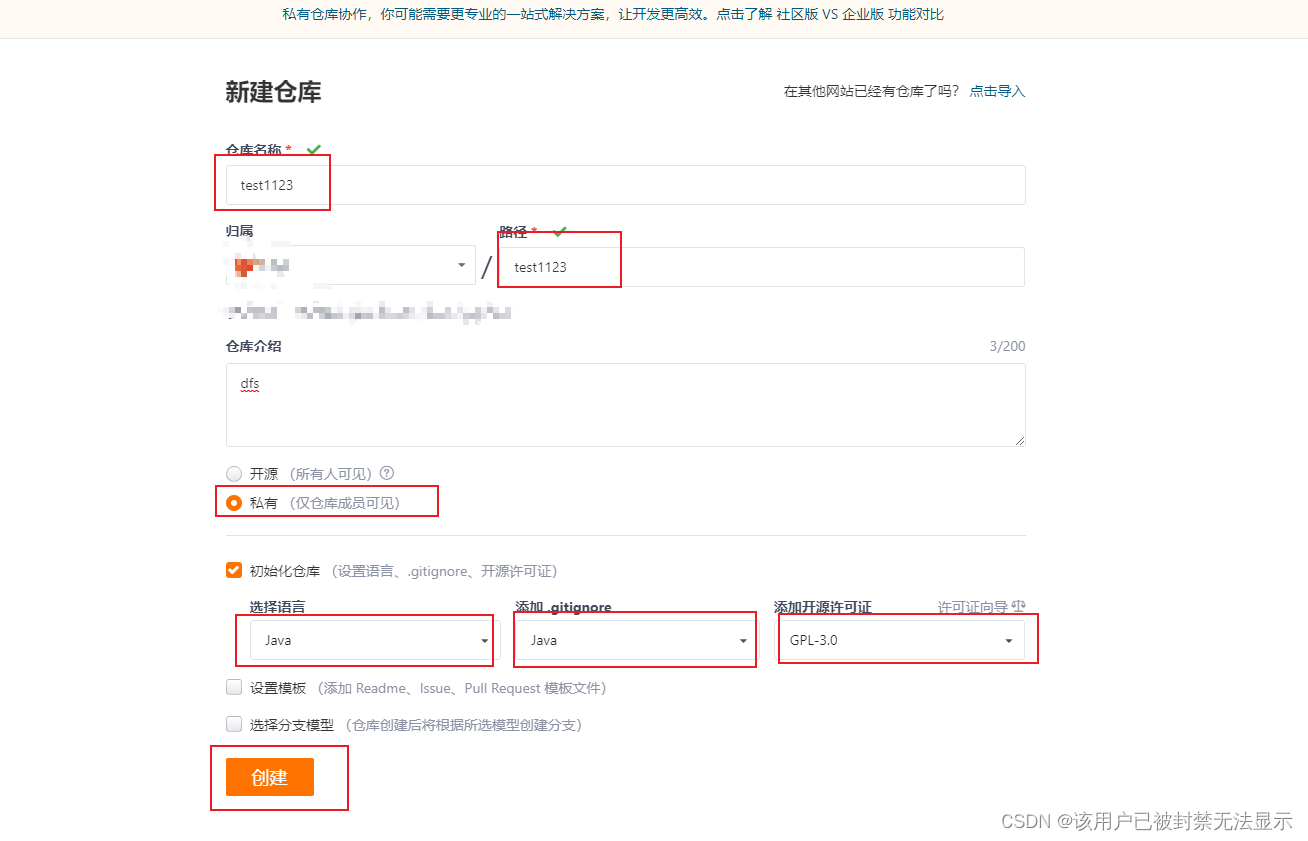
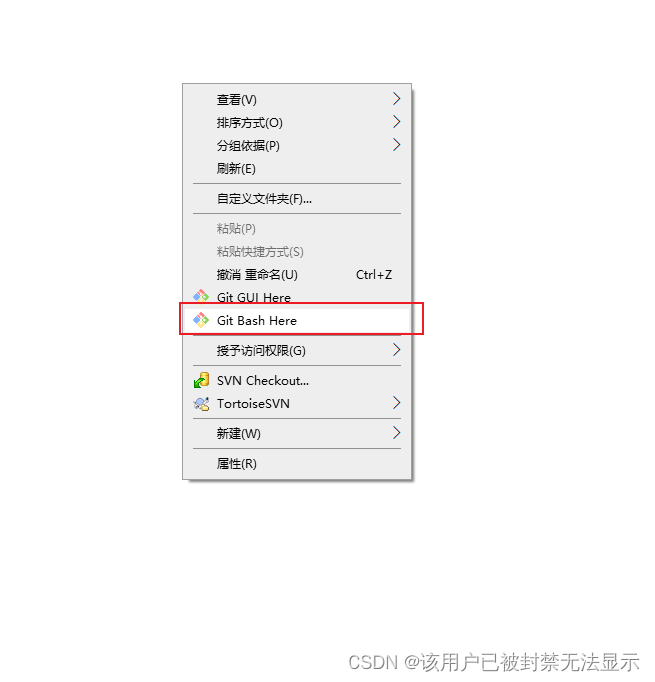
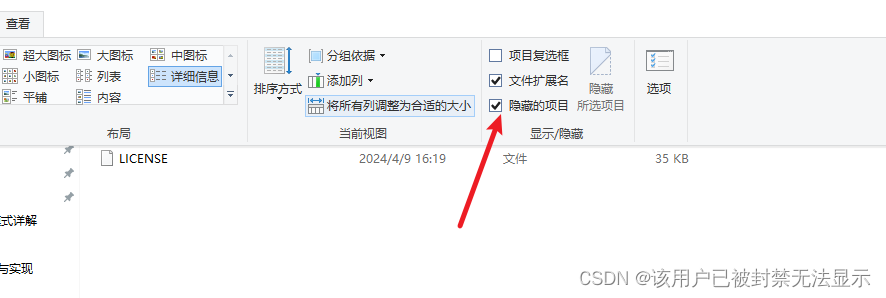
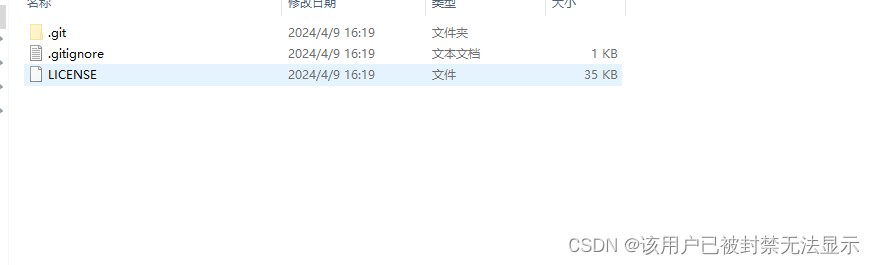
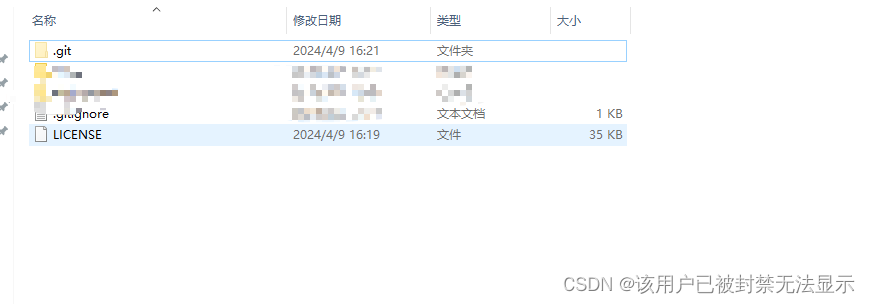
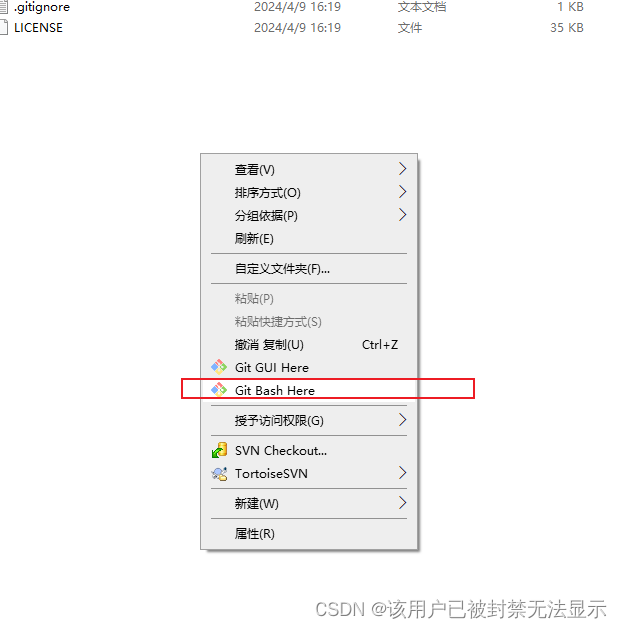
本地代码第一次提交到远程仓库gitee
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/803109.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
php curl发送文件请求
快手开发者文档:https://open.kuaishou.com/platform/openApi?menu20
1、body参数 Content-Type为 multipart/form-data public function sendPostFileRequest1($url,$file_path){// 初始化cURL会话$ch curl_init();// 设置目标URLcurl_setopt($ch, CURLOPT_URL,…
ssm033单位人事管理系统+jsp
单位人事管理系统设计与实现
摘 要
现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本单位人事管理系统就是在这样的大环境下诞生,其可以帮助管理者在短…
SpringMVC数据接收(全面/详细注释)
SpringMVC涉及组件:
DispatcherServlet : SpringMVC提供,我们需要使用web.xml配置使其生效,它是整个流程处理的核心,所有请求都经过它的处理和分发![ CEO ]HandlerMapping : SpringMVC提供,我们需要进行…
从零开始:一步步学习爬虫技术的实用指南(一)
从零开始:一步步学习爬虫技术的实用指南(一) Urllib1.什么是互联网爬虫2.爬虫核心3.爬虫的用途4.爬虫的分类4.1 通用爬虫:4.1 聚焦爬虫: 5.反爬手段5.1 User‐Agent:5.2.代理IP5.3.验证码访问5.4.动态加载网…
11.python的字典dict(下) 遍历字典,结构优化
11.python的字典dict(下)
遍历所有的键值对
items()方法是字典的一个内置方法,用于返回字典中所有键值对的视图(view)。它返回一个可迭代的对象,每个元素都是一个包含键和对应值的元组。
下面用一个例子来说明items()方法的用法…
Vue中Suspense组件详细介绍
<Suspense> 是一个内置组件,用来在组件树中协调对异步依赖的处理。它让我们可以在组件树上层等待下层的多个嵌套异步依赖项解析完成,并可以在等待时渲染一个加载状态。 异步依赖 要了解 <Suspense> 所解决的问题和它是如何与异步依赖进行交…
服务器负载均衡原理及算法
服务器负载均衡原理及算法
一、引言
随着互联网技术的飞速发展,网络服务的需求日益增长,单台服务器的性能往往难以满足大规模并发访问的需求。因此,服务器负载均衡技术应运而生,它能够有效地将网络请求分发到多台服务器上&#…
[C++/Linux] UDP编程
一. UDP函数 UDP(用户数据报协议,User Datagram Protocol)是一种无连接的网络协议,用于在互联网上交换数据。它允许应用程序发送数据报给另一端的应用程序,但不保证数据报能成功到达,也就是说,它…
Java常用类(二)
常用类(二)
Object类
超类,基类,所有类的直接或间接父类,位于继承树的最高层任何类,如没有书写extends显示继承某个类,都默认直接继承Object类,否则为间接继承Object类中所定义的方…
C语言题目:数组寻找最小绝对值
题目描述
输入10个数,找出其中绝对值最小的数,将它和最后一个数交换,然后输出这10个数。
输入格式
十个数
输出格式
交换后的十个数
样例输入
10 2 30 40 50 60 70 80 90 100
样例输出
10 100 30 40 50 60 70 80 90 2 代码解析 包含…
扫描IP开放端口该脚本用于对特定目标主机进行常见端口扫描(加载端口字典)或者指定端口扫描,判断目标主机开
扫描IP开放端口该脚本用于对特定目标主机进行常见端口扫描(加载端口字典)或者指定端口扫描,判断目标主机开
#/bin/bash #该脚本用于对特定目标主机进行常见端口扫描(加载端口字典)或者指定端口扫描,判断目标主机开放来哪些端口 #用telnet方式 IP$1 #IP119.254.3.28 #获得IP的前…
BUUCTF刷题十一道(12)SSTI专题一
文章目录 学习文章[Flask]SSTI[GWCTF 2019]你的名字[第三章 web进阶]SSTI[pasecactf_2019]flask_ssti[NewStarCTF 公开赛赛道]BabySSTI_One[Dest0g3 520迎新赛]EasySSTI[NewStarCTF 公开赛赛道]BabySSTI_Two[NewStarCTF 公开赛赛道]BabySSTI_Three[GYCTF2020]FlaskApp[CSCCTF 2…
List接口(1) | ArrayList
参考阅读:ArrayList 源码分析
一、特点
ArrayList 继承于 AbstractList ,实现了 List, RandomAccess, Cloneable, java.io.Serializable 这些接口,具有以下特点:
支持添加,删除和查找操作支持随机快速访问ÿ…
前端ocr技术:electron+vue3中使用tesseract插件识别图片中字符
同学们可以私信我加入学习群! 正文开始 前言一、electron各种csp问题二、试用插件总结 前言
项目需要ocr技术识别图片中的中文字符,本来这部分是后端的工作,但是因为各种原因,决定前端也做一个版本。
在ai时代之前,o…
基于spring boot的漫画之家系统
基于spring boot的漫画之家系统设计与实现 开发语言:Java
框架:springboot
JDK版本:JDK1.8
服务器:tomcat7
数据库:mysql 5.7(一定要5.7版本)
数据库工具:Navicat11
开发软件&…
pta L1-012 计算指数
L1-012 计算指数
分数 5 全屏浏览 切换布局
作者 陈越
单位 浙江大学
真的没骗你,这道才是简单题 —— 对任意给定的不超过 10 的正整数 n,要求你输出 2n。不难吧?
输入格式:
输入在一行中给出一个不超过 10 的正整数 n。
…
鲁棒线性模型估计(Robust linear model estimation)
鲁棒线性模型估计 1.RANSAC算法1.1 算法的基本原理1.2 迭代次数N的计算1.3 参考代码 参考文献 当数据中出现较多异常点时,常用的线性回归OLS会因为这些异常点的存在无法正确估计线性模型的参数: W ( X T X ) − 1 X T Y \qquad \qquad W(X^TX)^{-1}X^T…




)
)
 遍历字典,结构优化)


![[C++/Linux] UDP编程](http://pic.xiahunao.cn/[C++/Linux] UDP编程)

)

或者指定端口扫描,判断目标主机开)
SSTI专题一)

 | ArrayList)




)