目录
- 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
- 第四周:深层神经网络(Deep Neural Networks)
- 4.1 深层神经网络(Deep L-layer neural network)
- 4.2 前向传播和反向传播(Forward and backward propagation)
- 4.3 深层网络中的前向传播(Forward propagation in a Deep Network)
- 4.4 核对矩阵的维数(Getting your matrix dimensions right)
第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
第四周:深层神经网络(Deep Neural Networks)
4.1 深层神经网络(Deep L-layer neural network)
目前为止我们学习了只有一个单独隐藏层的神经网络的正向传播和反向传播,还有逻辑回归,并且你还学到了向量化,这在随机初始化权重时是很重要。
本周所要做的是把这些理念集合起来,就可以执行你自己的深度神经网络。
复习下前三周的课的内容:
1.逻辑回归,结构如下图左边。一个隐藏层的神经网络,结构下图右边:

注意,神经网络的层数是这么定义的:从左到右,由 0 开始定义,比如上边右图, x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3,这层是第 0 层,这层左边的隐藏层是第 1 层,由此类推。如下图左边是两个隐藏层的神经网络,右边是 5 个隐藏层的神经网络。

严格上来说逻辑回归也是一个一层的神经网络,而上边右图一个深得多的模型,浅与深仅仅是指一种程度。记住以下要点:
有一个隐藏层的神经网络,就是一个两层神经网络。记住当我们算神经网络的层数时,我们不算输入层,我们只算隐藏层和输出层。
但是在过去的几年中,DLI(深度学习学院 deep learning institute)已经意识到有一些函数,只有非常深的神经网络能学会,而更浅的模型则办不到。尽管对于任何给定的问题很难去提前预测到底需要多深的神经网络,所以先去尝试逻辑回归,尝试一层然后两层隐含层,然后把隐含层的数量看做是另一个可以自由选择大小的超参数,然后再保留交叉验证数据上评估,或者用你的开发集来评估。
我们再看下深度学习的符号定义:
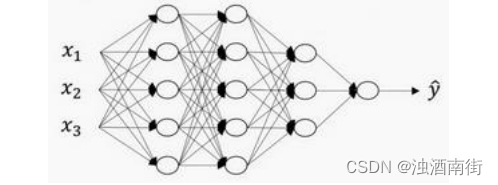
上图是一个四层的神经网络,有三个隐藏层。我们可以看到,第一层(即左边数过去第二层,因为输入层是第 0 层)有 5 个神经元数目,第二层 5 个,第三层 3 个。
我们用 L 表示层数,上图:𝐿 = 4,输入层的索引为“0”,第一个隐藏层 n [ 1 ] n^{[1]} n[1] = 5,表示有 5个隐藏神经元,同理 n [ 2 ] n^{[2]} n[2] = 5, n [ 3 ] n^{[3]} n[3] = 3, n [ 4 ] n^{[4]} n[4]= n [ L ] n^{[L]} n[L] =1(输出单元为 1)。而输入层, n [ 0 ] = n x = 3 n^{[0]} =n_x = 3 n[0]=nx=3。
在不同层所拥有的神经元的数目,对于每层 l 都用 a [ l ] a^{[l]} a[l]来记作 l 层激活后结果,我们会在后面看到在正向传播时,最终能你会计算出 a [ l ] a^{[l]} a[l]。
通过用激活函数 g计算 z [ l ] z^{[l]} z[l],激活函数也被索引为层数l,然后我们用 w [ l ] w^{[l]} w[l]来记作在 l 层计算 z [ l ] z^{[l]} z[l]值的权重。类似的, z [ l ] z^{[l]} z[l]里的方程b[l]也一样。
最后总结下符号约定:
输入的特征记作𝑥,但是𝑥同样也是 0 层的激活函数,所以 x = a [ 0 ] x = a^{[0]} x=a[0]。
最后一层的激活函数,所以 a [ L ] a^{[L]} a[L]是等于这个神经网络所预测的输出结果。
4.2 前向传播和反向传播(Forward and backward propagation)
之前我们学习了构成深度神经网络的基本模块,比如每一层都有前向传播步骤以及一个相反的反向传播步骤,这次视频我们讲讲如何实现这些步骤。
先讲前向传播,输入 a [ l − 1 ] a^{[l−1]} a[l−1],输出是 a [ l ] a^{[l]} a[l],缓存为 z [ l ] z^{[l]} z[l];从实现的角度来说我们可以缓存下 w [ l ] w^{[l]} w[l]和 b [ l ] b^{[l]} b[l],这样更容易在不同的环节中调用函数。

所以前向传播的步骤可以写成: z [ l ] = W [ l ] ⋅ a [ l − 1 ] + b [ l ] , a [ l ] = g [ l ] ( z [ l ] ) z^{[l]} = W^{[l]}⋅ a^{[l−1]} + b^{[l]} , a^{[l]} = g^{[l]}(z^{[l]}) z[l]=W[l]⋅a[l−1]+b[l],a[l]=g[l](z[l])
向量化实现过程可以写成: Z [ l ] = W [ l ] ⋅ A [ l − 1 ] + b [ l ] , A [ l ] = g [ l ] ( Z [ l ] ) Z^{[l]}= W^{[l]}⋅ A^{[l−1]} + b^{[l]} , A^{[l]} = g^{[l]}(Z^{[l]}) Z[l]=W[l]⋅A[l−1]+b[l],A[l]=g[l](Z[l])
前向传播需要喂入 A [ 0 ] A^{[0]} A[0]也就是X,来初始化;初始化的是第一层的输入值。 a [ 0 ] a^{[0]} a[0]对应于一个训练样本的输入特征,而 A [ 0 ] A^{[0]} A[0]对应于一整个训练样本的输入特征,所以这就是这条链的第一个前向函数的输入,重复这个步骤就可以从左到右计算前向传播。
下面讲反向传播的步骤:输入为𝑑𝑎[𝑙],输出为𝑑𝑎[𝑙−1],𝑑𝑤[𝑙], 𝑑𝑏[𝑙]

所以反向传播的步骤可以写成:
(1) d z [ l ] = d a [ l ] ∗ g [ l ] ′ ( z [ l ] ) dz^{[l]} = da^{[l]}∗ g^{[l]'}(z^{[l]}) dz[l]=da[l]∗g[l]′(z[l])
(2) d w [ l ] = d z [ l ] ⋅ a [ l − 1 ] dw^{[l]} = dz^{[l]}⋅ a^{[l−1]} dw[l]=dz[l]⋅a[l−1]
(3) d b [ l ] = d z [ l ] db^{[l]} = dz^{[l]} db[l]=dz[l]
(4) d a [ l − 1 ] = w [ l ] T ⋅ d z [ l ] da^{[l−1]} = w^{[l]T}⋅ dz^{[l]} da[l−1]=w[l]T⋅dz[l]
(5) d z [ l ] = w [ l + 1 ] T d z [ l + 1 ] ∗ g [ l ] ′ ( z [ l ] ) dz^{[l]} = w^{[l+1]T}dz^{[l+1]}*g^{[l]'}(z^{[l]}) dz[l]=w[l+1]Tdz[l+1]∗g[l]′(z[l])
式子(5)由式子(4)带入式子(1)得到,前四个式子就可实现反向函数。
向量化实现过程可以写成:
(6) d Z [ l ] = d A [ l ] ∗ g [ l ] ′ ( Z [ l ] ) dZ^{[l]} = dA^{[l]}∗ g^{[l]'}(Z^{[l]}) dZ[l]=dA[l]∗g[l]′(Z[l])
(7) d W [ l ] = 1 m d Z [ l ] ⋅ A [ l − 1 ] T dW^{[l]} =\frac{1}{m}dZ^{[l]}⋅A^{[l−1]T} dW[l]=m1dZ[l]⋅A[l−1]T
(8) d b [ l ] = 1 m n p . s u m ( d z [ l ] , a x i s = 1 , k e e p d i m s = T r u e ) db^{[l]} =\frac{1}{m}np.sum(dz[l], axis = 1, keepdims =True) db[l]=m1np.sum(dz[l],axis=1,keepdims=True)
(9) d A [ l − 1 ] = W [ l ] T . d Z [ l ] dA^{[l−1]} = W^{[l]T}. dZ[l] dA[l−1]=W[l]T.dZ[l]
总结一下:

第一层你可能有一个 ReLU 激活函数,第二层为另一个 ReLU 激活函数,第三层可能是sigmoid 函数(如果你做二分类的话),输出值,用来计算损失;这样你就可以向后迭代进行反向传播求导来求 d w [ 3 ] , d b [ 3 ] , d w [ 2 ] , d b [ 2 ] , d w [ 1 ] , d b [ 1 ] dw^{[3]},db^{[3]} ,dw^{[2]} ,db^{[2]} ,dw^{[1]} ,db^{[1]} dw[3],db[3],dw[2],db[2],dw[1],db[1]。在计算的时候,缓存会把 z [ 1 ] , z [ 2 ] , z [ 3 ] z^{[1]},z^{[2]},z^{[3]} z[1],z[2],z[3]传递过来,然后回传 d a [ 2 ] , d a [ 1 ] da^{[2]},da^{[1]} da[2],da[1] ,可以用来计算 d a [ 0 ] da^{[0]} da[0],但我们不会使用它,这里讲述了一个三层网络的前向和反向传播,还有一个细节没讲就是前向递归——用输入数据来初始化,那么反向递归(使用 Logistic 回归做二分类)——对 A [ l ] A^{[l]} A[l] 求导。
4.3 深层网络中的前向传播(Forward propagation in a Deep Network)
跟往常一样,我们先来看对其中一个训练样本 x 如何应用前向传播,之后讨论向量化的版本。
第一层需要计算 z [ 1 ] = w [ 1 ] x + b [ 1 ] , a [ 1 ] = g [ 1 ] ( z [ 1 ] ) z^{[1]} = w^{[1]}x + b^{[1]},a^{[1]} = g^{[1]}(z^{[1]}) z[1]=w[1]x+b[1],a[1]=g[1](z[1])(x可以看做 a [ 0 ] a^{[0]} a[0])
第二层需要计算 z [ 2 ] = w [ 2 ] a [ 1 ] + b [ 2 ] , a [ 2 ] = g [ 2 ] ( z [ 2 ] ) z^{[2]} = w^{[2]}a^{[1]} + b^{[2]},a^{[2]} = g^{[2]}(z^{[2]}) z[2]=w[2]a[1]+b[2],a[2]=g[2](z[2])
以此类推,第四层为 z [ 4 ] = w [ 4 ] a [ 3 ] + b [ 4 ] , a [ 4 ] = g [ 4 ] ( z [ 4 ] ) z^{[4]} = w^{[4]}a^{[3]} + b^{[4]},a^{[4]} = g^{[4]}(z^{[4]}) z[4]=w[4]a[3]+b[4],a[4]=g[4](z[4])
前向传播可以归纳为多次迭代 z [ l ] = w [ l ] a [ l − 1 ] + b [ l ] , a [ l ] = g [ l ] ( z [ l ] ) z^{[l]} = w^{[l]}a^{[l−1]} + b^{[l]},a^{[l]} = g^{[l]}(z^{[l]}) z[l]=w[l]a[l−1]+b[l],a[l]=g[l](z[l])。

向量化实现过程可以写成: Z [ l ] = W [ l ] a [ l − 1 ] + b [ l ] , A [ l ] = g [ l ] ( Z [ l ] ) ( A [ 0 ] = X ) Z^{[l]} = W^{[l]}a^{[l−1]} + b^{[l]},A^{[l]} = g^{[l]}(Z^{[l]}) (A^{[0]} = X) Z[l]=W[l]a[l−1]+b[l],A[l]=g[l](Z[l])(A[0]=X)
这里只能用一个显式 for 循环,𝑙从 1 到𝐿,然后一层接着一层去计算。下一节讲的是避免代码产生 BUG,我所做的其中一件非常重要的工作。
4.4 核对矩阵的维数(Getting your matrix dimensions right)
当实现深度神经网络的时候,其中一个我常用的检查代码是否有错的方法就是拿出一张纸过一遍算法中矩阵的维数。
𝑤的维度是(下一层的维数,前一层的维数),即 w [ l ] : ( n [ l ] , n [ l − 1 ] ) w^{[l]}: (n^{[l]},n^{[l−1]}) w[l]:(n[l],n[l−1]);
𝑏的维度是(下一层的维数,1),即: b [ l ] : ( n [ l ] , 1 ) b^{[l]}: (n^{[l]},1) b[l]:(n[l],1);
z [ l ] , a [ l ] : ( n [ l ] , 1 ) z^{[l]},a^{[l]}:(n^{[l]}, 1) z[l],a[l]:(n[l],1);
d w [ l ] dw^{[l]} dw[l]和 w [ l ] w^{[l]} w[l]维度相同, d b [ l ] db^{[l]} db[l]和 b [ l ] b^{[l]} b[l]维度相同,且w和b向量化维度不变,但𝑧,𝑎以及𝑥的维度会向量化后发生变化。

向量化后:
Z [ l ] Z^{[l]} Z[l]可以看成由每一个单独的 Z [ l ] Z^{[l]} Z[l]叠加而得到, Z [ l ] = ( z [ l ] [ 1 ] , z [ l ] [ 2 ] , z [ l ] [ 3 ] , … , z [ l ] [ m ] ) Z^{[l]} = (z^{[l][1]},z^{[l][2]},z^{[l][3]},…,z^{[l][m]}) Z[l]=(z[l][1],z[l][2],z[l][3],…,z[l][m]),𝑚为训练集大小,所以 Z [ l ] Z^{[l]} Z[l]的维度不再是 ( n [ l ] , 1 ) (n^{[l]}, 1) (n[l],1),而是 ( n [ l ] , m ) (n^{[l]}, m) (n[l],m)。
A [ l ] : ( n [ l ] , m ) , A [ 0 ] = X = ( n [ l ] , m ) A^{[l]}:(n^{[l]}, m),A^{[0]} = X = (n^{[l]}, m) A[l]:(n[l],m),A[0]=X=(n[l],m)
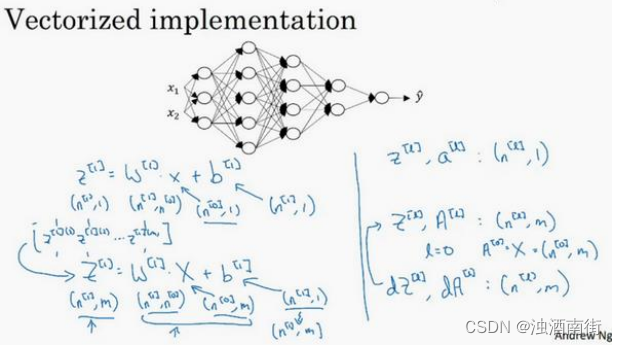
在你做深度神经网络的反向传播时,一定要确认所有的矩阵维数是前后一致的,可以大大提高代码通过率。下一节我们讲为什么深层的网络在很多问题上比浅层的好。


)








)



 代理机制以及小技巧)
)
)
测量指南》)
