一文详解二叉搜索树

数据结构-二叉查找树

前言

**摘自百度百科：**二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。

简而言之，二叉查找树（Binary Search Tree）又称为 二叉搜索树、二叉排序树。它是一种 对搜索和排序都有用的特殊二叉树。而 红黑树、AVL树 都是特殊的二叉树（自平衡二叉树）。

定义

当一个二叉树为特殊二叉树时，势必会满足以下条件：

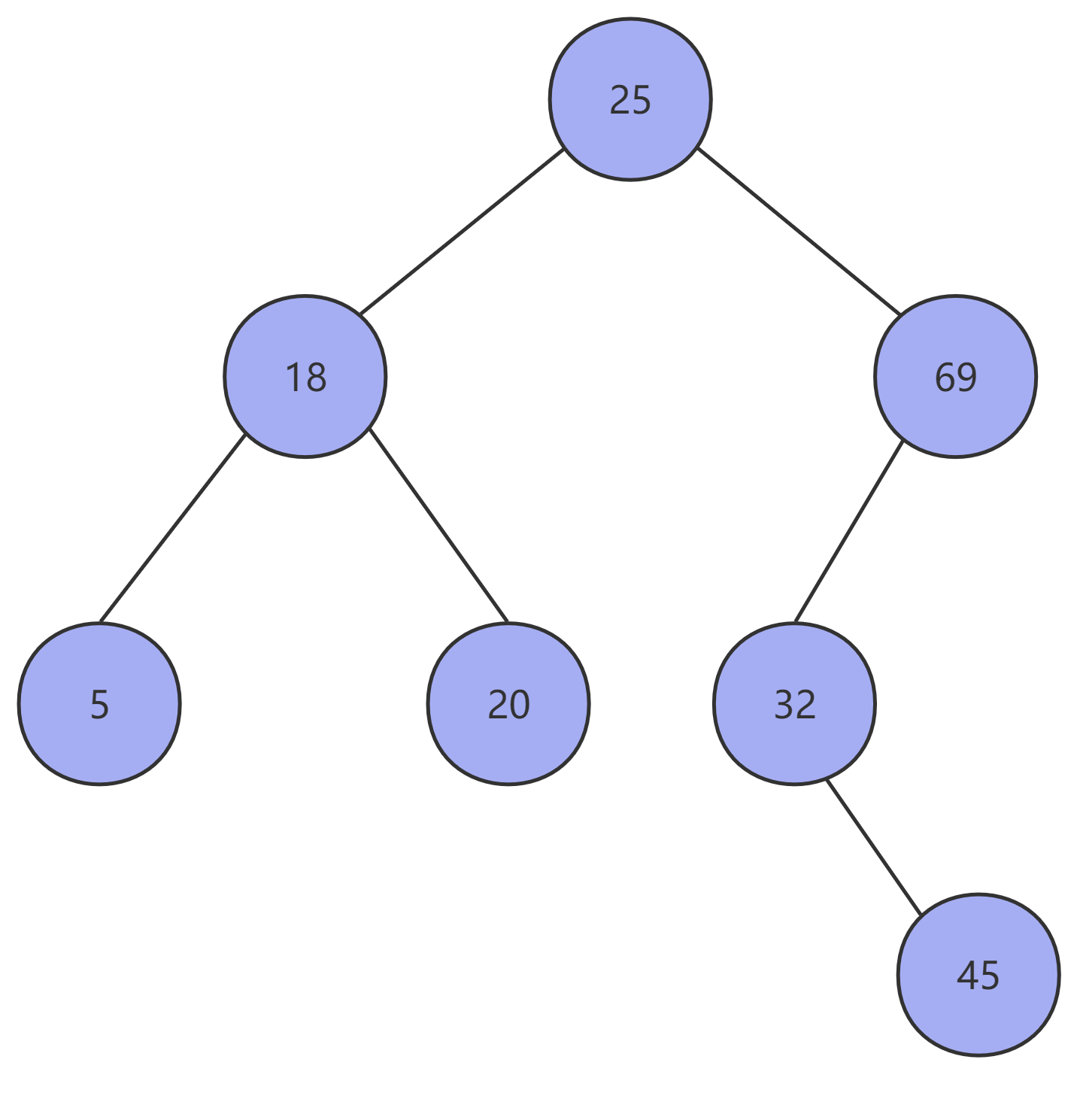
  • 当其左子树不为空时，其左子树上所有的节点的值均小于根节点的值。
  • 当其右子树不为空时，其右子树上所有节点的值均大于根节点的值。
  • 该树上的所有子树（左右子树）均为一颗二叉查找树。

其结构如下图所示：

未命名文件.png

应用场景

  • 电商系统的商品搜索与排序

  • 秒杀系统中的库存管理

  • 社交系统中的好友关系管理

  • 文件系统中的目录和文件管理

  • 图书管理系统中的书籍检索

以上应用场景只是举例说明，并不代表全部，二叉搜索树的应用场景非常广泛，当系统需要高效的执行：搜索、排序、插入、删除、范围查询等操作时均可考虑使用 二叉查找树。

查询

在 二叉查找树 中，查询方式类似于 二分查找法，每次递归查询时都可以缩小一半的查找范围，其查询的速率也较高。

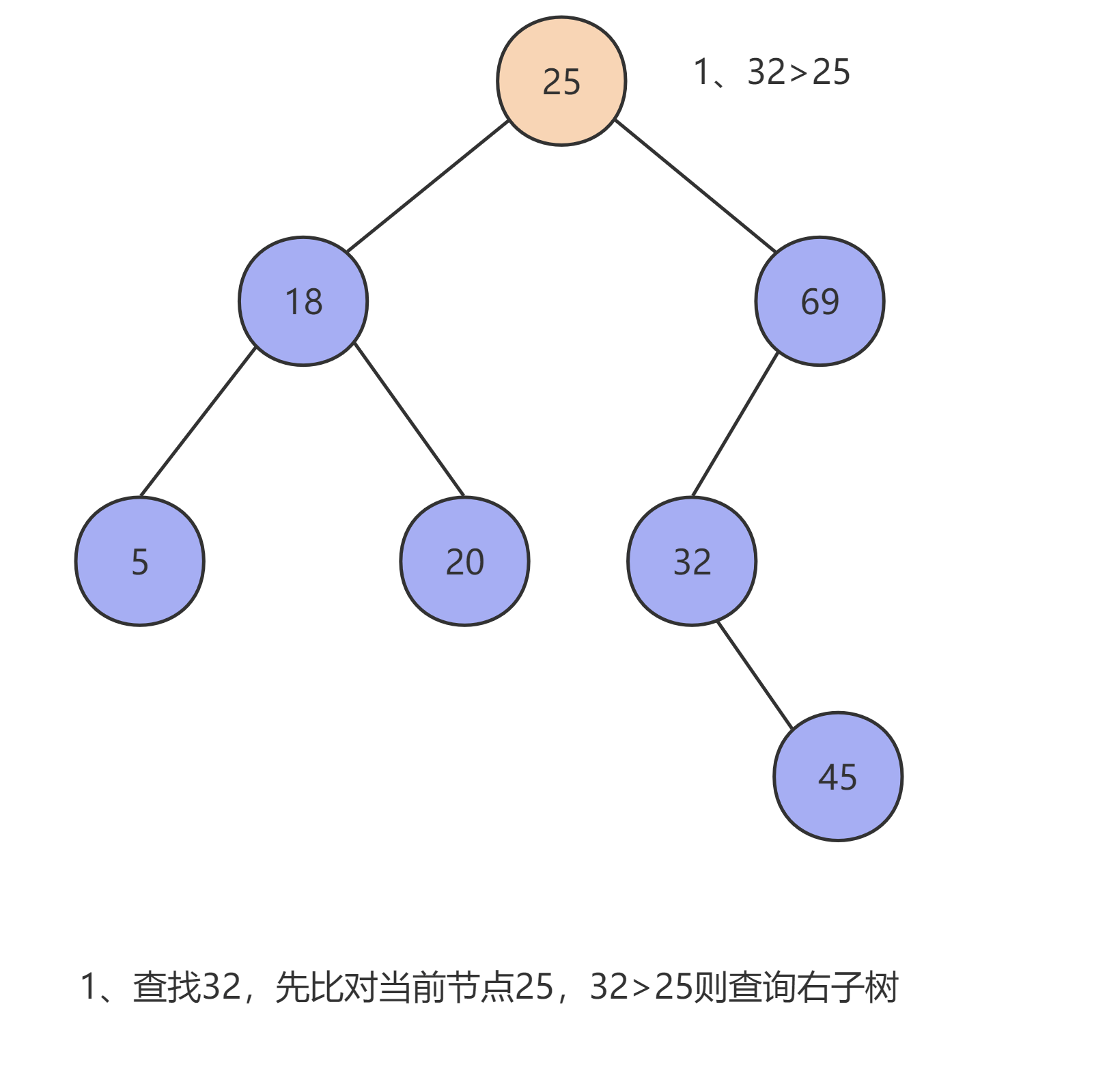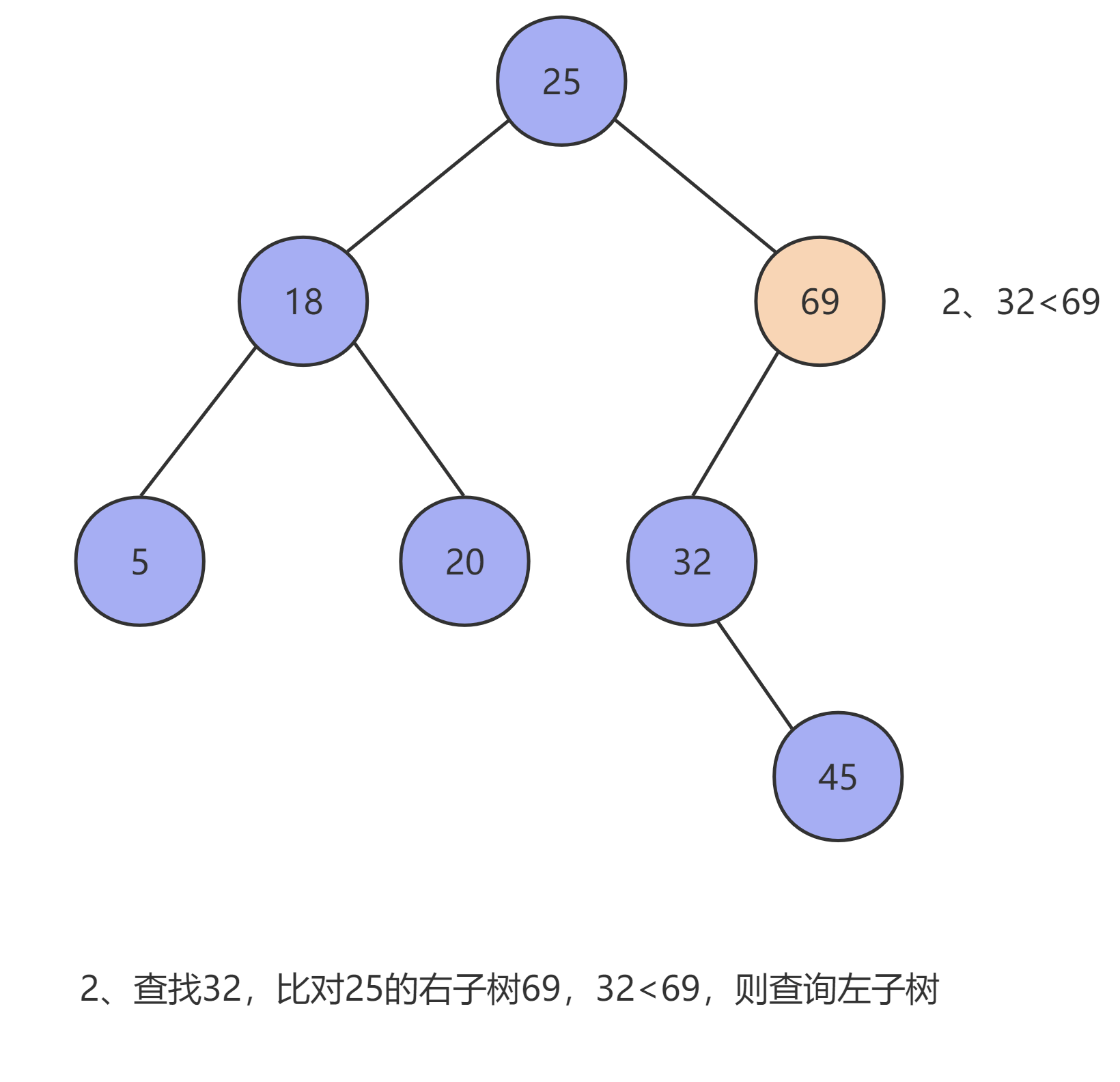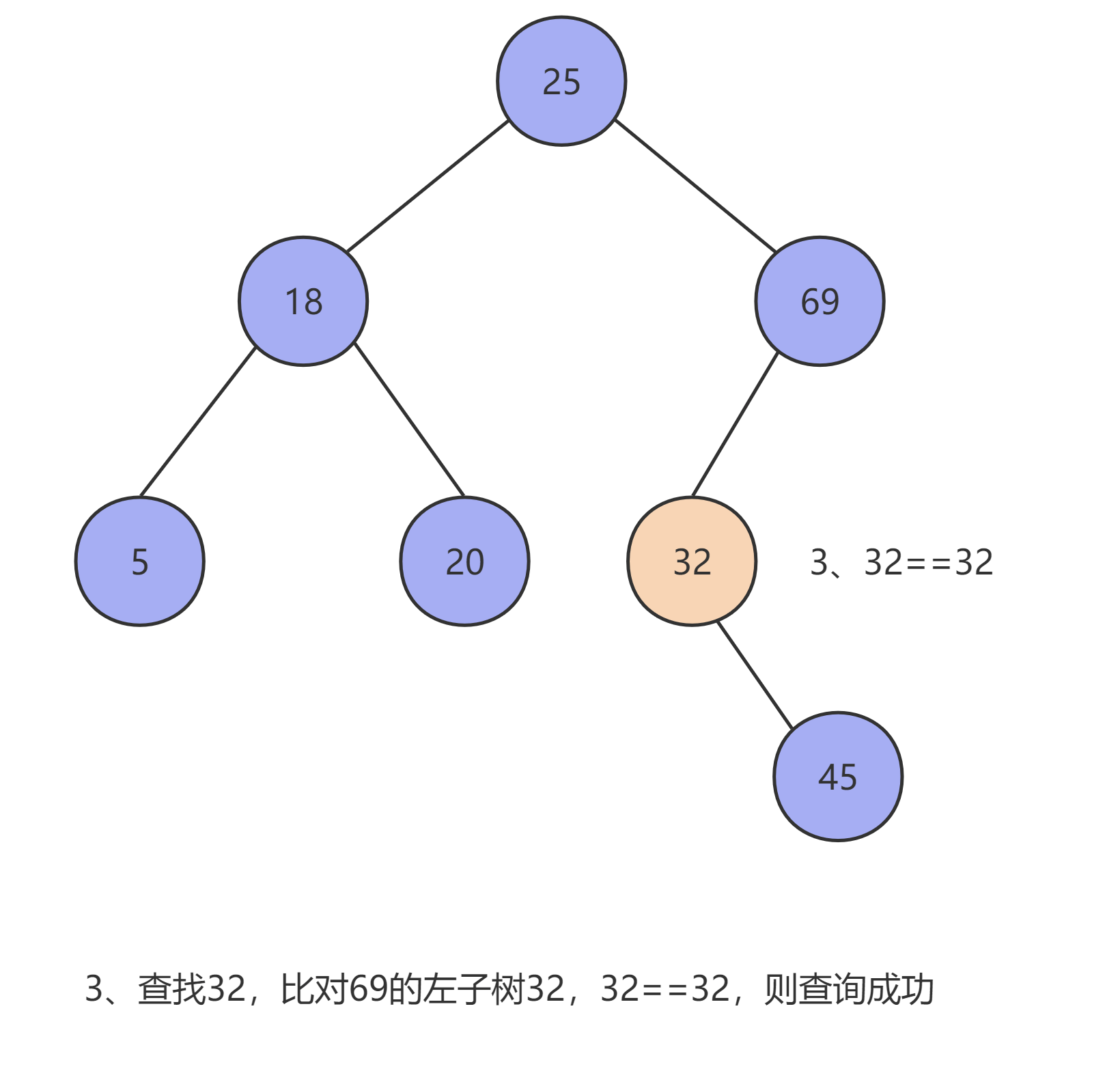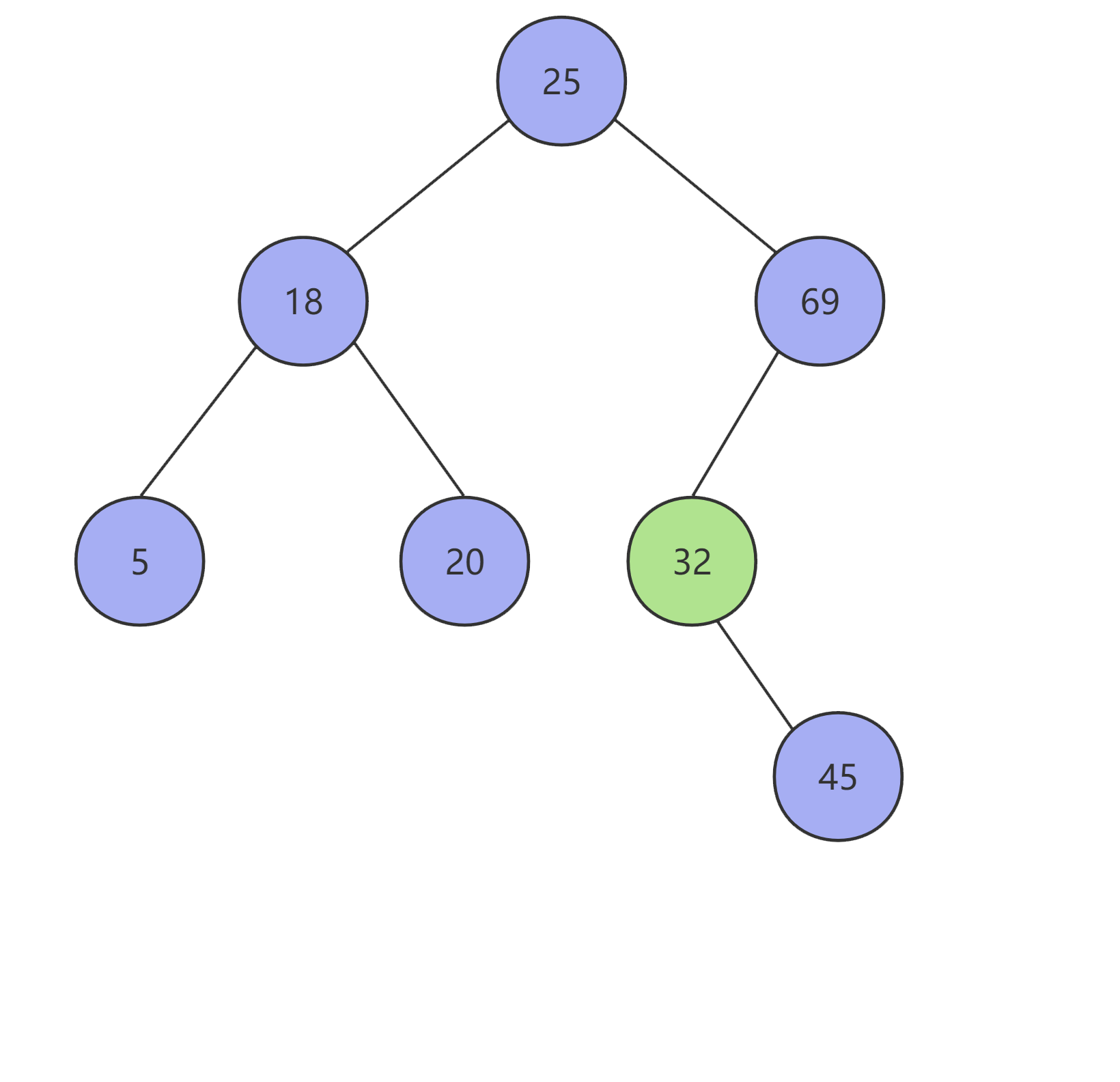
当使用 二叉查找树 去查找某条数据时（设这条数据为 x ，当前数据为 T ），其会按以下流程循环查询，直至查出结果，如果查到叶子节点仍无匹配数据时则返回 null ：

  • 当 x == T 时，则 T 就是我们要查询的数据，返回 T 。
  • 当 x < T 时，则去查询当前节点的左子树进行比对。
  • 当 x > T 时，则去查询当前节点的右子树进行比对。

以上流程如下图所示：

未命名文件.gif

实体

根据上述的二叉查找树的概念，我们可以抽离出来一个模型，代码如下：

public class Node {public Integer data;public Node parent;public Node left;public Node right;public Node(){}public Node(Integer data) {this.data = data;}public Integer getData() {return data;}public void setData(Integer data) {this.data = data;}public Node getParent() {return parent;}public void setParent(Node parent) {this.parent = parent;}public Node getLeft() {return left;}public void setLeft(Node left) {this.left = left;}public Node getRight() {return right;}public void setRight(Node right) {this.right = right;}@Overridepublic String toString() {return "Node{" +"data=" + data +", parent=" + parent +", left=" + left +", right=" + right +'}';}
}

二叉查找树

建立好我们的实体后，我们可以单独创建一个类来进行二叉查找树的一些操作。

public class BinarySearchTree {private final Logger log = Logger.getLogger(BinarySearchTree.class.getName());private Node root;/*** @param data 需要查找的值* @return {@link Node}* @date 2023-09-16 10:53* @author Bummon* @description 二叉树查找*/public Node findDataByBTS(Node node, Integer data) {while (Objects.nonNull(node)) {if (Objects.equals(data, node.data)) {return node;} else if (data < node.data) {//左子树node = node.left;} else if (data > node.data) {//右子树node = node.right;}}return null;}
}

测试

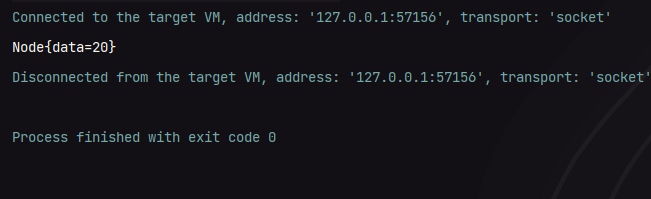
public class Main {public static void main(String[] args) {BinarySearchTree bst = new BinarySearchTree();Node root = new Node(50);Node node1 = new Node(30);root.setLeft(node1);Node node2 = new Node(70);root.setRight(node2);Node node3 = new Node(20);node1.setLeft(node3);Node node4 = new Node(40);node1.setRight(node4);Node node5 = new Node(60);node2.setLeft(node5);Node node6 = new Node(80);node2.setRight(node6);Node node = bst.findDataByBTS(root, 25);System.out.println(node);}
}

最终我们可以得到如下结果：

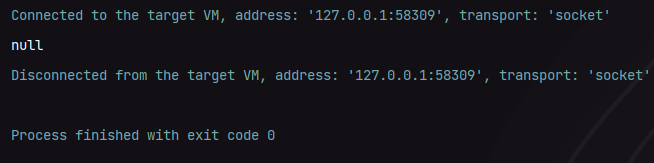
image.png

我们也可以去查找一个不存在的数据测试一下，这里使用25来测试，如下图所示：

image.png

新增

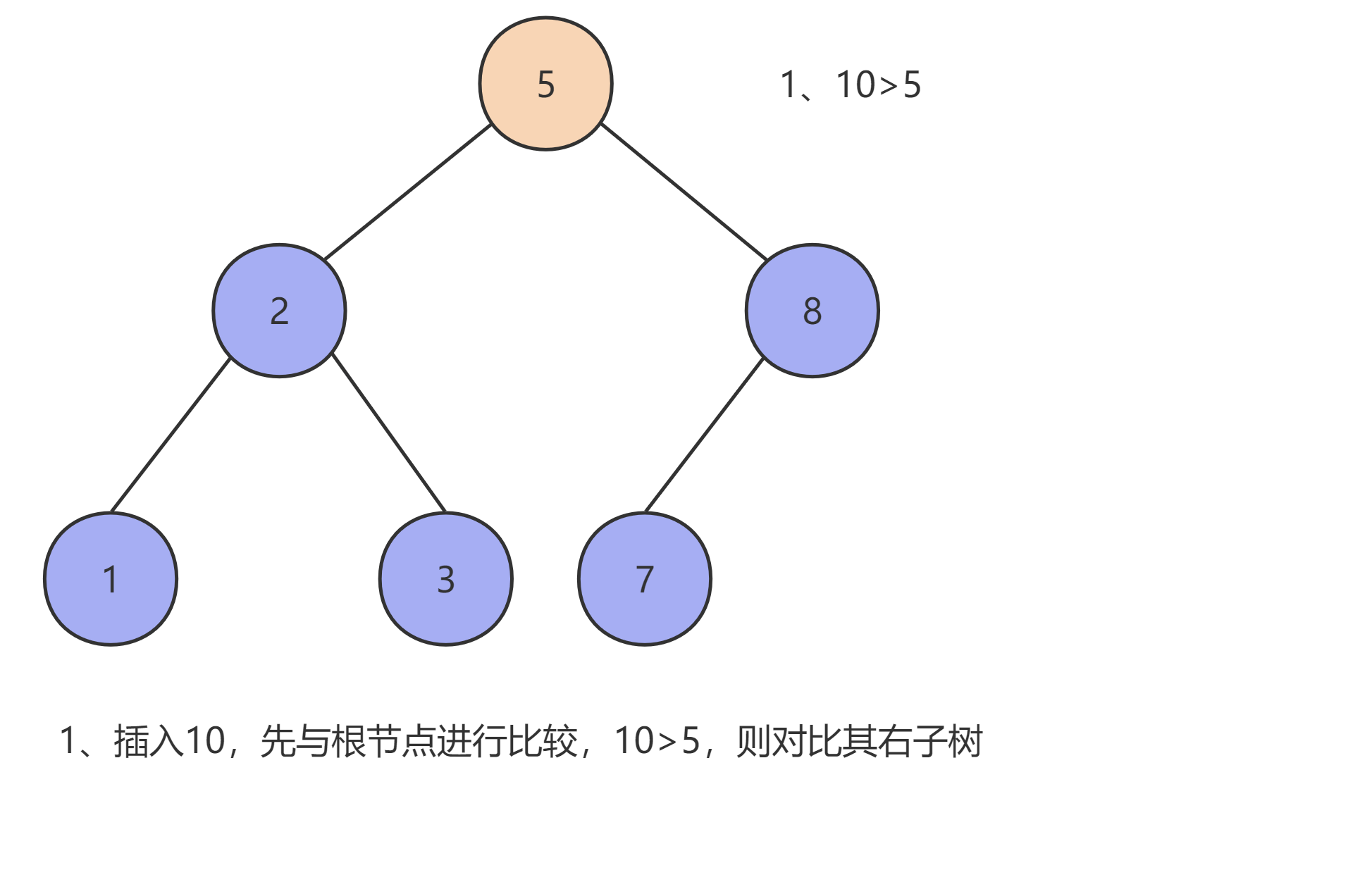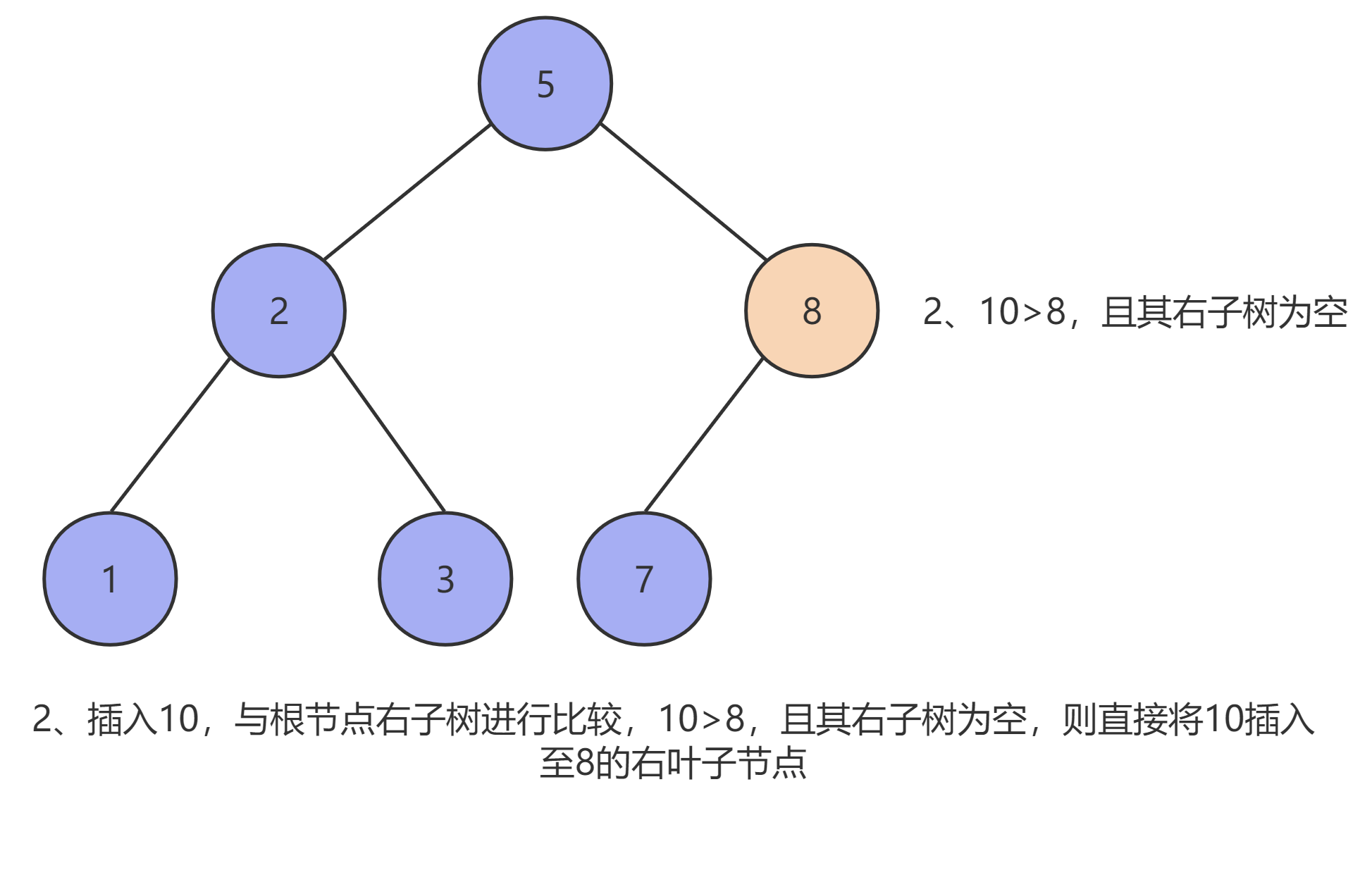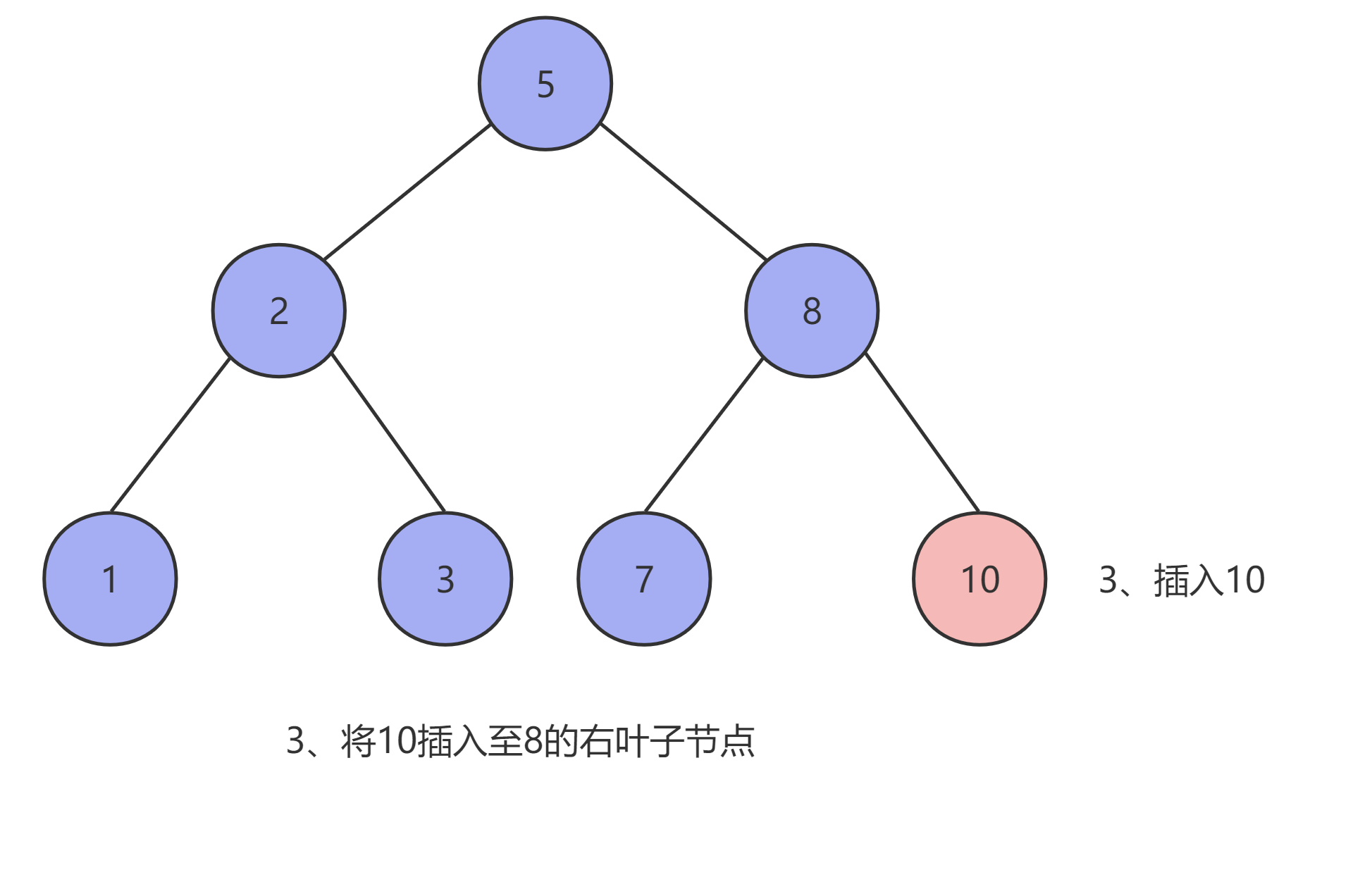
由于二叉查找树的特性，我们首先需要先找到插入元素的插入位置，设需要插入的元素为 x ，当前节点为 T ，则：

  • 当二叉查找树为空时，创建一个新的节点，并将 x 放到根节点的位置，且其 左子树 和 右子树 均为空。
  • 当二叉树不为空且 x < T 时，将 x 插入 T 的左子树中。
  • 当二叉树不为空且 x > T 时，将 x 插入 T 的右子树中。

如下图所示：

未命名文件-(1).gif

代码实现

为了方便测试这里也增加了一个分层遍历的方法

/*** @param data 需要插入的值* @date 2023-09-16 10:54* @author Bummon* @description 插入节点*/public void insert(int data) {if (Objects.isNull(root)) {root = initNode(root);root.setData(data);} else {recursionInsert(root, data);}}/*** @param data 需要插入的值* @date 2023-09-16 10:54* @author Bummon* @description 插入节点*/public void insert(int data) {if (Objects.isNull(root)) {root = initNode(root);root.setData(data);} else {recursionInsert(root, data);}}/*** @param node 插入节点* @param data 需要插入的值* @return {@link Node}* @date 2023-09-16 10:53* @author Bummon* @description 私有化插入节点*/private Node recursionInsert(Node node, int data) {if (Objects.isNull(node)) {node = new Node(data);}if (data < node.data) {node.left = recursionInsert(node.left, data);node.left.parent = node;} else if (data > node.data) {node.right = recursionInsert(node.right, data);node.right.parent = node;}return node;}/*** @param node 需要初始化的节点* @return {@link Node}* @date 2023-09-16 10:52* @author Bummon* @description 初始化节点*/private Node initNode(Node node) {if (Objects.isNull(node)) {return new Node();}return node;}/*** @date 2023-09-16 14:18* @author Bummon* @description 分层遍历树*/public void levelOrderTraversal() {Queue<Node> nodes = new ConcurrentLinkedDeque<>();nodes.add(root);while (nodes.size() > 0) {Node currNode = nodes.poll();if (Objects.nonNull(currNode.left)) {nodes.add(currNode.left);}if (Objects.nonNull(currNode.right)) {nodes.add(currNode.right);}String msg = String.format("{%s}(%s)", currNode.data, currNode.parent != null ? currNode.parent.data : "null");log.info(msg);}}

测试

public class Main {public static void main(String[] args) {BinarySearchTree bst = new BinarySearchTree();bst.insert(50);bst.insert(30);bst.insert(20);bst.insert(40);bst.insert(70);bst.insert(60);bst.insert(80);bst.levelOrderTraversal();}
}

我们执行的结果如下：

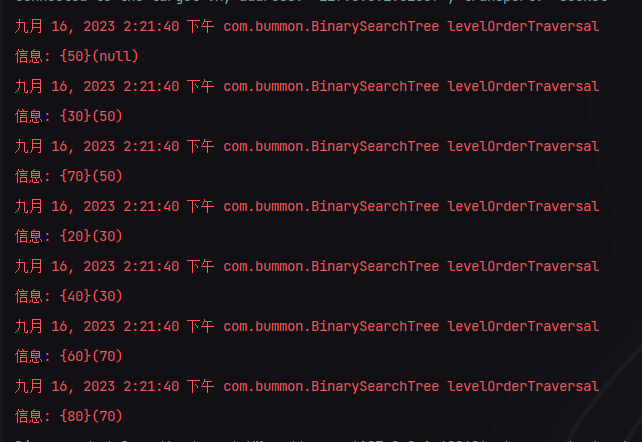
image.png

如果以树的形式来展示的话长以下这样：

未命名文件 (4).png

删除

当我们想要从二叉查找中删除某个节点时，会经历以下历程：首先先要查找到我们要删除的节点位置，如果查找成功则继续执行删除操作，否则直接返回。而删除操作会有以下四种情况：

  1. 当被删除的节点左右子树均为空时，则直接删除即可。
  2. 当被删除的节点只有左子树时，即右子树为空，则直接删除，并将其左子树的节点代替被删除的节点，代替后删除其左子树原先的节点。
  3. 当被删除的节点只有右子树时，即左子树为空，则直接删除，并将其右子树的节点代替被删除的节点，代替后删除其右子树原先的节点。
  4. 当被删除的节点左右子树均不为空时，则将其直接前驱或直接后续作为替代节点，将被删除的节点删除后，将替代节点放至被删除的节点位置，代替后删除替代节点原先的节点。

如下所示：

未命名文件-(1).gif

代码实现

public void deleteNode(int data) {if (root == null) {System.out.println("删除失败，为空树");}Node delNode = root;Node parent = null;//首先要先找到待删除的节点while (delNode != null) {if (data < delNode.data) {parent = delNode;delNode = delNode.left;} else if (data > delNode.data) {parent = delNode;delNode = delNode.right;} else {break;}}if (delNode == null) {log.info("Not Found " + data);return;}//删除节点左子树为空if (delNode.left == null) {if (delNode == root) {root = delNode.right;} else if (delNode == parent.left) {parent.left = delNode.left;} else {parent.right = delNode.right;}} else if (delNode.right == null) {//删除节点右子树为空if (delNode == root) {root = delNode.left;} else if (delNode == parent.left) {parent.left = delNode.left;} else {parent.right = delNode.left;}} else {//删除有节点左右子树均不为空Node nextParent = delNode;Node next = delNode.right;while (next.left != null) {nextParent = next;next = next.left;}delNode.data = next.data;if (nextParent == delNode) {nextParent.right = next.right;} else {nextParent.left = next.right;}}}

测试

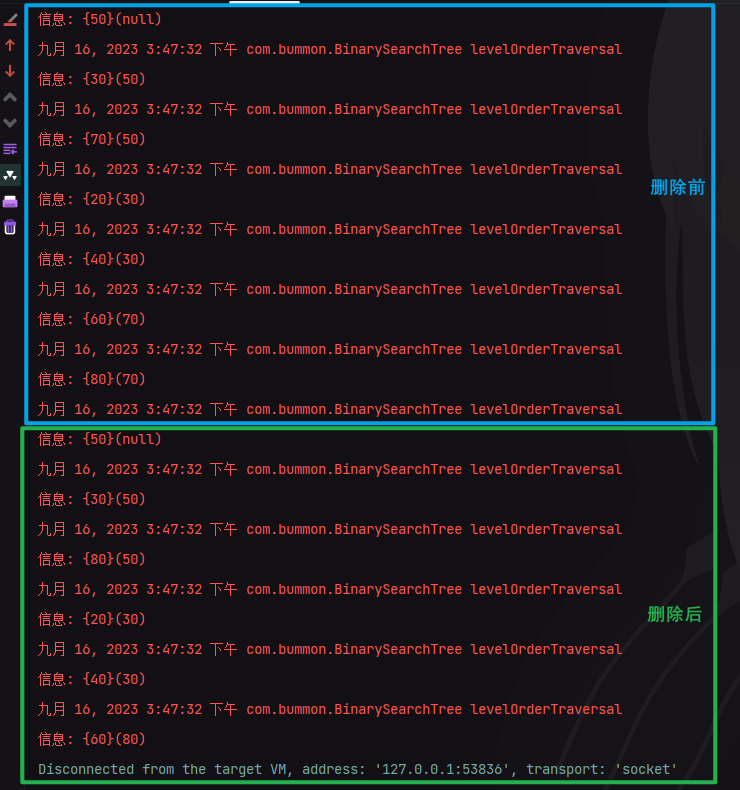
public class Main {public static void main(String[] args) {BinarySearchTree bst = new BinarySearchTree();bst.insert(50);bst.insert(30);bst.insert(20);bst.insert(40);bst.insert(70);bst.insert(60);bst.insert(80);bst.levelOrderTraversal();bst.deleteNode(70);bst.levelOrderTraversal();}
}

我们会得到如下结果：

image.png

总结

二叉查找树 是一种特殊的二叉树，其搜索速率较快，类似于 二分查找法 ，其在查询时先确定查找值的查询范围，再逐步缩小范围，直至查出结果或查完所有节点仍未找到返回 null 。其最坏情况为遍历所有节点，即时间复杂度为 O(n)，空间复杂度为 O(1)。

推荐

关注博客和公众号获取最新文章

Bummon’s Blog ｜ Bummon’s Home ｜ 公众号

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/80134.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

JDK8特性——接口增强函数式接口Optional方法引用

JDK8特性——接口增强函数式接口Optional方法引用

文章目录 接口增强默认方法静态方法 函数式接口SupplierConsumerFunctionPredicate Optional 类以前对null 的处理Optional的基本使用Optional的常用方法 方法引用方法引用的格式对象名::方法名类名::静态方法名类名::引用实例方法类名::构造器数组::构造器 接口增强 在JDK8之…
阅读更多...
智能远程监考方案助力企业考试化繁为简

智能远程监考方案助力企业考试化繁为简

在音视频数字化之旅中&#xff0c;轻装上阵。 近年来&#xff0c;在数字化浪潮之下&#xff0c;远程考试频繁成为各领域热词&#xff0c;各企业也纷纷改革求新&#xff0c;将原本的企业内部考试转移到线上&#xff0c;从而获取更低廉的组考成本&#xff0c;更高的管理效率&…
阅读更多...
深度学习基础之梯度下降

深度学习基础之梯度下降

1. 引言 梯度下降是一种用于最小化&#xff08;或最大化&#xff09;损失函数的优化算法。它是机器学习和深度学习中的一个关键概念&#xff0c;通常用于调整学习算法中的参数。 梯度下降背后的核心思想是迭代调整参数以最小化损失函数。它的工作原理是计算损失函数相对于每个…
阅读更多...
【LeetCode-中等题】18. 四数之和

【LeetCode-中等题】18. 四数之和

文章目录 题目方法一&#xff1a;双指针&#xff08;定2动2&#xff09; 题目 方法一&#xff1a;双指针&#xff08;定2动2&#xff09; 这题可以参考【LeetCode-中等题】15. 三数之和 区别在于&#xff0c;三数之和只需要用一个for循环定住一个数&#xff0c;然后设置两个前…
阅读更多...
数据结构与算法(C语言版)P4---顺序表、链表总结

数据结构与算法(C语言版)P4---顺序表、链表总结

顺序表和链表&#xff08;双向带头链表&#xff09;的区别 顺序表&#xff1a; 优点&#xff1a; 支持随机访问。需要随机访问结构支持算法可以很好的使用。cpu高速缓存利用率&#xff08;命中率&#xff09;更高。存储密度高 缺点&#xff1a; 头部中部插入删除时间效率低。…
阅读更多...
合宙Air724UG LuatOS-Air LVGL API控件-窗口 (Window)

合宙Air724UG LuatOS-Air LVGL API控件-窗口 (Window)

窗口 (Window) 分 享导出pdf 示例代码 win lvgl.win_create(lvgl.scr_act(), nil) lvgl.win_set_title(win, "Window title") -- close_btn lvgl.win_add_btn_right(win, "\xef\x80\x8d") -- --lvgl.obj_set_event_cb(cl…
阅读更多...
典型数据结构-图，图的存储、基本操作和遍历

典型数据结构-图，图的存储、基本操作和遍历

图 引自&#xff1a;《数据结构教程》。 概念 图可以使得元素之间的关系是 多对多。图中任意两个数据元素之间都可能存在连接关系。图作为一种数据结构&#xff0c;可以表达数据元素之间广泛存在着的更为复杂的关系。在众多应用之中&#xff0c;如电子线路分析、工程计划分析、…
阅读更多...
Junit单元测试异常处理方法

Junit单元测试异常处理方法

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 Junit单元测试异常处理方法 前言案例准备一、类方法内处理异常二、测试方法中处理异常1.try/catch/finally 语句2.Test(expected)3.ExpectedException 前言 提示&#xff1a…
阅读更多...
深度解析shell脚本的命令的原理之mv

深度解析shell脚本的命令的原理之mv

mv 是 Unix 或 Linux 中的一个基本命令&#xff0c;用于移动或重命名文件和目录。以下是对这个命令的深度解析&#xff1a; 基本操作&#xff1a;mv 命令的基本操作是将一个或多个源文件或目录移动到一个目标文件或目录&#xff0c;或者重命名源文件或目录。这是通过改变文件系…
阅读更多...
银河麒麟--国产操作系统-九五小庞

银河麒麟--国产操作系统-九五小庞

那么&#xff0c;我国国产操作系统现状到底如何呢&#xff1f; 自 1999 年徐冠华部长一语点破我们的产业软肋之后&#xff0c;国产操作系统起步于国家“七五”计划期间&#xff0c;目前国产操作系统均是基于Linux内核进行的二次开发&#xff0c;中国国产操作系统进入Linux元年…
阅读更多...
CSS：隐藏移动端的滚动条的方式

CSS：隐藏移动端的滚动条的方式

目录 方式一&#xff1a;-webkit-scrollbar方式二&#xff1a;overflow方式三&#xff1a;clip-path方式四&#xff1a;mask 遮罩总结参考 移动端开发中&#xff0c;有一个横向滚动元素&#xff0c;产品告诉我不需要滚动条&#xff0c;我说这个简单&#xff0c;隐藏一下不就行了…
阅读更多...
iText实战--在现有PDF上工作

iText实战--在现有PDF上工作

6.1 使用PdfReader读取PDF 检索文档和页面信息 D:/data/iText/inAction/chapter03/image_direct.pdf Number of pages: 1 Size of page 1: [0.0,0.0,283.0,416.0] Rotation of page 1: 0 Page size with rotation of page 1: Rectangle: 283.0x416.0 (rot: 0 degrees) Is reb…
阅读更多...
深度思考ES面经

深度思考ES面经

1 推荐文章 2万字详解&#xff0c;吃透 Elasticsearch 2 什么是倒排索引&#xff0c;为什么这么叫&#xff1f; 倒排索引&#xff08;Inverted Index&#xff09;是一种为快速全文搜索而设计的数据结构。它被广泛应用于搜索引擎&#xff0c;其中 Elasticsearch&#xff08;简…
阅读更多...
C# 扫描并读取图片中的文字（.NET Core)

C# 扫描并读取图片中的文字（.NET Core)

本文介绍如何通过C# 程序来扫描并读取图片中的文字&#xff0c;这里以创建一个.Net Core程序为例。下面是具体步骤&#xff0c;供参考。 程序测试环境&#xff1a; Visual Studio版本要求不低于2017 图片扫描工具&#xff1a;Spire.OCR for .NET 图片格式&#xff1a;png&…
阅读更多...
JSP ssm 网上求职管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计

JSP ssm 网上求职管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计

一、源码特点 JSP ssm 网上求职管理系统是一套完善的web设计系统&#xff08;系统采用SSM框架进行设计开发&#xff0c;springspringMVCmybatis&#xff09;&#xff0c;对理解JSP java编程开发语言有帮助&#xff0c;系统具有完整的源代码和数据库&#xff0c;系统主要采…
阅读更多...
zookeeper最基础教程

zookeeper最基础教程

文章目录 一、简介1、工作机制2、特点3、数据结构4、应用场景5、选举机制 二、软件安装1、单机版安装2、集群安装3、配置参数解读(zoo.cfg)4、ZK集群启动脚本 三、命令行操作1、语法2、使用3、节点相关4、监听器原理5、节点删除与查看 三、写数据流程 一、简介 1、工作机制 官…
阅读更多...
SQL优化--排序优化（order by）

SQL优化--排序优化（order by）

Using filesort : 通过表的索引或全表扫描&#xff0c;读取满足条件的数据行&#xff0c;然后在排序缓冲区sort buffer中完成排序操作&#xff0c;所有不是通过索引直接返回排序结果的排序都叫 FileSort 排序。 Using index : 通过有序索引顺序扫描直接返回有序数据&#xff0c…
阅读更多...
1031. 两个非重叠子数组的最大和

1031. 两个非重叠子数组的最大和

1031. 两个非重叠子数组的最大和 原题链接&#xff1a;完成情况&#xff1a;解题思路&#xff1a;参考代码&#xff1a; 原题链接&#xff1a; 1031. 两个非重叠子数组的最大和 https://leetcode.cn/problems/maximum-sum-of-two-non-overlapping-subarrays/description/ 完…
阅读更多...
【C语言】指针的进阶（一）

【C语言】指针的进阶（一）

目录 前言 1. 字符指针 2. 指针数组 3. 数组指针 3.1 数组指针的定义 3.2 &数组名VS数组名 3.3 数组指针的使用 4. 数组参数、指针参数 4.1 一维数组传参 4.2 二维数组传参 4.3 一级指针传参 4.4 二级指针传参 5. 函数指针 前言 指针在C语言中可谓是有着举足轻重的…
阅读更多...
Arm发布 Neoverse V2 和 E2：下一代 Arm 服务器 CPU 内核

Arm发布 Neoverse V2 和 E2：下一代 Arm 服务器 CPU 内核

9月14日&#xff0c;Arm发布了新的处理器内核&#xff1a;V2和E2&#xff0c;在官网已经可以看到相关的TRM 手册了。。 四年前&#xff0c;Arm发布了Neoverse系列的CPU设计。Arm决定加大力度进军服务器和边缘计算市场&#xff0c;专门为这些市场设计Arm CPU内核&#xff0c;而…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023