【Leetcode每日一题】递归 - 验证二叉搜索树（难度⭐⭐）（53）

1. 题目解析

题目链接：98. 验证二叉搜索树

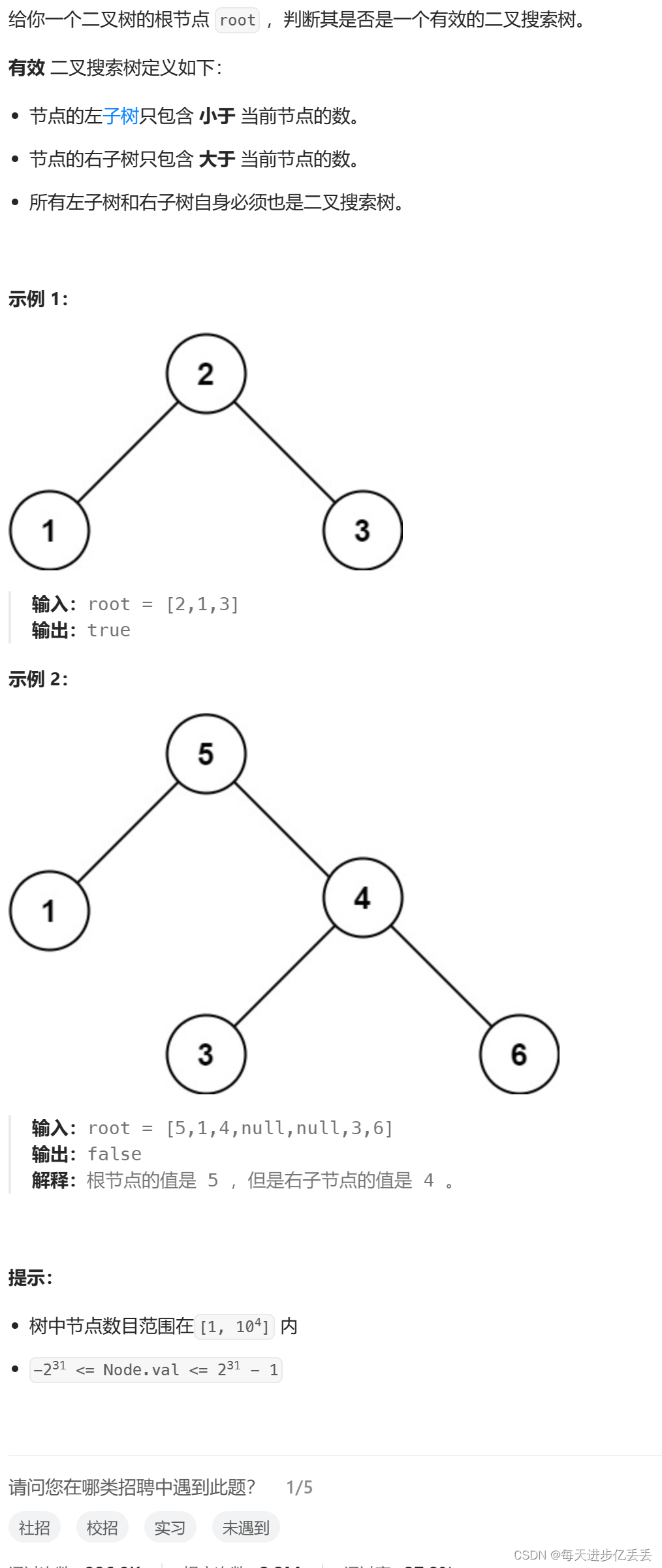
这个问题的理解其实相当简单，只需看一下示例，基本就能明白其含义了。

2.算法原理

中序遍历是二叉树遍历中的一种重要方式，它按照左子树、根节点、右子树的顺序访问每个节点。这种方式特别常用于二叉搜索树的验证和相关题目中。二叉搜索树有一个特殊的性质：其中序遍历的结果一定是一个严格递增的序列。

想要验证一棵二叉树是否为二叉搜索树，我们可以借助中序遍历。在遍历的过程中，我们可以记录当前访问节点的前驱节点的值，并与当前节点的值进行比较，以确保它们是递增的。

下面是一个简单的算法流程，帮助我们理解这个过程：

初始化前驱节点值：
在开始遍历之前，我们需要一个变量prev来记录中序遍历中前驱节点的值。这个变量在开始时可以设置为一个无穷小的值，因为我们希望从最小的值开始比较。
定义中序遍历的递归函数：
这个函数会接收当前遍历的节点root作为参数。
- 递归出口：
  如果当前节点root为空（即已经遍历到了叶子节点的下方），则返回true，表示这一部分子树是满足二叉搜索树条件的。
- 递归判断左子树：
  首先，我们需要递归地判断左子树是否为二叉搜索树。我们可以使用一个变量retleft来标记左子树的验证结果。
- 判断当前节点：
  接下来，我们要判断当前节点是否满足二叉搜索树的性质。如果当前节点的值大于prev（即当前值大于前一个访问的节点的值），那么说明当前节点满足条件，我们可以将retcur标记为true；如果当前节点的值小于等于prev，则说明不满足条件，将retcur标记为false。
- 更新前驱节点值：
  在判断完当前节点后，我们需要更新prev的值为当前节点的值，以便在遍历下一个节点时进行比较。
- 递归判断右子树：
  最后，我们需要递归地判断右子树是否为二叉搜索树，并使用retright来标记右子树的验证结果。
汇总结果：
只有当左子树、当前节点和右子树都满足二叉搜索树的性质（即retleft、retcur和retright都为true）时，我们才能说整棵树是一个二叉搜索树，并返回true。否则，返回false。

通过这种方式，我们可以有效地利用中序遍历来验证一棵二叉树是否为二叉搜索树。这种方法不仅逻辑清晰，而且在实际应用中也非常有效。

3.代码编写

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*///二叉搜索树中序遍历是一个有序序列
class Solution 
{long prev = LONG_MIN; 
public:bool isValidBST(TreeNode* root) {if(!root) return true;bool left = isValidBST(root->left);//判断左子树是二souif(left == false) return false;//判断当前层是二搜bool cur = false;if(root->val > prev) cur = true;if(cur == false) return false;prev = root->val;bool right = isValidBST(root->right);//判断右子树是二搜return left && right && cur;}
};