目录

1 t 检验的定义

1.1 来自维基百科和百度百科

1.2 别名

1.3 和其他检验的区别

2 适用情况：

2.1 关于样本情况

2.2 适合检查的情况

2.2.1 单样本均值检验（One-sample t-test）

2.2.2  两独立样本均值检验（Independent two-sample t-test）

2.2.3 配对样本均值检验（Dependent t-test for paired samples）

2.2.4 回归系数的显著性检验（t-test for regression coefficient significance）

3 构造T检验量 t-stat

3.1  t 统计量是什么？

3.1.1 t统计量公式

3.1.2  几个核心统计量的推导

3.2 t 统计量的另外一个公式，线性回归里每个参数的t值

3.3  构造t 统计量

3.3.1 单样本的t，构造过程

3.3.2 双样本的t，构造过程

3.3.3 配对样本t检验

3.4 t统计量的意义

4 t分布

4.1 T分布曲线，类正态分布

4.2 和正态分布的区别

5 实操查表，T值表

5.1 查表方法

5.2 T值表

5.3 判断标准

6  例题

6.1 先获得关键参数信息

6.2 进行h0 h1假设

6.3 计算t值

6.4 根据双边检验显著度α/2,查表得到t值，然后比较

6.5 得到结论

参考文章

---

1 t 检验的定义

1.1 来自维基百科和百度百科

• 学生t 检验（英语：Student's t-test）是指零假设成立时的任一检验统计有学生t分布的统计假设检验，属于参数统计。
• 学生t检验常作为检验一群来自正态分配总体的独立样本之期望值是否为某一实数，或是二（两）群来自正态分配总体的独立样本之期望值的差是否为某一实数。
• 举个简单的例子，在某个学校中我们可以从某个年级中随机抽样一群男生，以检验该年级男生与全校男生之身高差异程度是否如我们所假设的某个值。

1.2 别名

• t检验
• 学生t检验
• Student t-test

1.3 和其他检验的区别

• T检验和Z检查，都是比较均值差异的，而不是比较方差齐性的，也就是都是比较 均值齐性的，也可以叫成 Homogeneity of  Average ？
• 而F检验，是检测方差齐性，Homogeneity of Variances，就是检查两者的方差是不是相同

2 适用情况：

2.1 关于样本情况

• t检验，适合样本数里<30 或大都可以
• 但是Z只适应样本数量比较大的时候

2.2 适合检查的情况

2.2.1 单样本均值检验（One-sample t-test）

• 用于检验 总体方差未知、正态数据或近似正态的 单样本的均值 是否与 已知的总体均值相等

2.2.2  两独立样本均值检验（Independent two-sample t-test）

• 用于检验 两对独立的 正态数据或近似正态的 样本的均值 是否相等，这里可根据总体方差是否相等分类讨论

2.2.3 配对样本均值检验（Dependent t-test for paired samples）

• 用于检验 一对配对样本的均值的差 是否等于某一个值

2.2.4 回归系数的显著性检验（t-test for regression coefficient significance）

• 用于检验 回归模型的解释变量对被解释变量是否有显著影响

3 构造T检验量 t-stat

3.1  t 统计量是什么？

3.1.1 t统计量公式

• t-stat= t=(average(x)-u) / (s/✔n)
• t 检验量，比较的是均值average(x)
  •  单样本t 检验量，比较的是均值average(x) 和u的差异
  •  量样本t 检验量，比较的是均值average(x1) 和average(x2)

3.1.2  几个核心统计量的推导

• t 检验量
• 因为核心是 average(x)，所以其标准差为 (s/✔n)
  • 如果   X                                 ~N(u,δ) , 符合正态分布
  • 那么  average(X)                  ~N(u,δ/✔n) ,符合正态分布,average(x) ~N(u,s✔n)
  • 那么   average(X)-u / (δ/✔n)    ~N(0,1)  符合标准正态分布 
• (n-1)s**2符合k2分布
• t = average(X)-u / (δ/✔n)  就是构造的一个符合标准正态分布的t变量

3.2 t 统计量的另外一个公式，线性回归里每个参数的t值

• 每个回归系数的t值  → t-统计量=回归系数 / 回归系数标准误差 
• 如果有多组样本，SE 标准误是标准差SD的平均值, SE=SD/✔n
• 回归系数标准误（standard error of regression coefficient）

3.3  构造t 统计量

3.3.1 单样本的t，构造过程

3.3.2 双样本的t，构造过程

3.3.3 配对样本t检验

3.4 t统计量的意义

• T统计值是用来判断参数的显著程度的
• 应用回归预测法时应首先确定变量之间是否存在相关关系。但是如果变量之间不存在相关关系，对这些变量应用回归预测法就会得出错误的结果。
• 查表要根据，自由度df，显著度α
• 如果T值，小于查表所得T值，那么就认为落在大概率的区间，接受原假设H0

4 t分布

4.1 T分布曲线，类正态分布

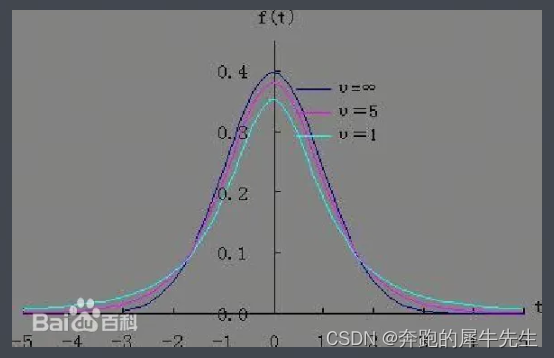
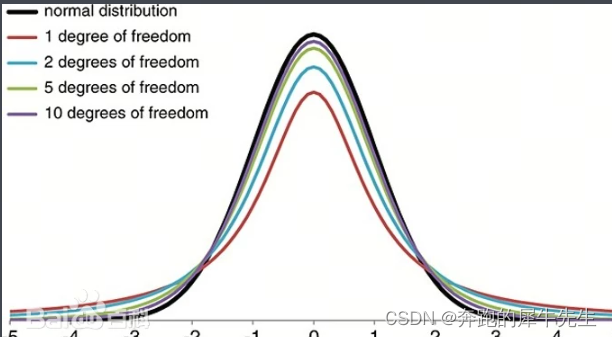
4.2 和正态分布的区别

• 在概率论和统计学中，t-分布（t-distribution）用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知或者在样本数量足够多时，则应该用正态分布来估计总体均值。 [1]
• t分布曲线形态与n（确切地说与自由度df）大小有关。与标准正态分布曲线相比，自由度df越小，t分布曲线愈平坦，曲线中间愈低，曲线双侧尾部翘得愈高；自由度df愈大，t分布曲线愈接近正态分布曲线，当自由度df=∞时，t分布曲线为标准正态分布曲线。

5 实操查表，T值表

5.1 查表方法

• 需要查表
• 自由度n-1，显著度α
• 查t界值表中自由度为n-1，双侧α，如果是单边检验，那么查到的t(α, n-1)
• 查t界值表中自由度为n-1，双侧α，如果是双边检验，那么查到的t(α/2, n-1)
• 然后查到的t值，作为比较的参数指标

5.2 T值表

• 纵列是自由度df
• 横列是概率p,也就是显著度α
• 表里查的不是p,而是t值，不同概率对应的 t的边界值

5.3 判断标准

• 一般，Z和T检验量的实际值越大，对应的p概率值就越小！就越要拒绝相等的假设

6  例题

6.1 先获得关键参数信息

• 样本均值，方差
• 总体均值
• 样本数量
• 自由度，要剔除统计量的影响

6.2 进行h0 h1假设

• h0 假设两者均值相同

6.3 计算t值

6.4 根据双边检验显著度α/2,查表得到t值，然后比较

6.5 得到结论

• t检验量    1.774823935    <    2.032        
• 考虑正态曲线分布                
• 可以知道，这个t落在大概率的曲线下方部分                                
• 因此接受假设h0，认为两者没有明显差异    

参考文章

一文详解t检验 - 知乎不排除书写错误，文中几乎所有的公式都给出了详细的证明。 仅为教科书相关内容，不代表学术前沿。关于实验的设计与分析，可看 混乱数据分析：设计的实验引子t检验（t test）又称学生t检验（Student t-test）可以说…https://zhuanlan.zhihu.com/p/138711532https://zhuanlan.zhihu.com/p/138711532