思路：本题还是直觉，想使得整体的数组和最大，需要每一次取反都尽可能使的全局最优。先将数组排序，然后如果有负数，优先总左边开始，将最小的负数逐渐往上取反，这样可以使得和尽可能增大。当取到没有负数后，如果是0则直接返回目前结果。如果没有0，则后面就不断重复第一个最小正数即可。时间复杂度O(nlogn)。在具体代码实现上可以简洁一些。

class Solution {
public:int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(),nums.end());int sum=0;for(int i=0;i<nums.size();i++){//先求和sum+=nums[i];}for(int i=0;i<k;i++){if(nums[i]<0){if(i==nums.size()-1){//还有一种情况，那就是已经到达最后一个负数，而且后面没有0和正数//这时只需要考虑反转目前这个绝对值最小的负数k-i次而且需要breakif((k-i)%2==1){//反转次数为奇数sum-=(2*nums[i]);}break;}sum-=(2*nums[i]);//普遍情况，直接反转负数}else if(nums[i]==0){break;//如果已经到等于0的情况说明后面怎么变都是这个sum了}else{//正数，后面的所有都是在第一个最小正数循环int minNum=nums[i];if(i>0&&nums[i-1]<0&&(-nums[i-1])<nums[i]){//不是第一个正数，前面一个为负数，这时的反转对象为他们的最小绝对值minNum=-nums[i-1];}if((k-i)%2==1){//(k-i)为剩下还要反转的次数,如果是奇数则需要反转，如果是偶数则直接不变sum-=(2*minNum);}break;}}return sum;}
};

然而我在具体代码实现的时候发现了很多小问题，并不是右手就行，需要对当前值为负数、0、正数分开讨论。其中0最容易；负数还需要考虑是不是数组最后一个数（数组全负），然后计算最后一个元素的剩余反转次数；而正数还需要比较最小正数和最大负数的绝对值，然后再根据剩余反转次数反转。
看完标答，发现如果在开始排序的时候按照绝对值大小排，就可以直接修改原数组，然后最后的反转也十分容易。标答是先全部反转完毕后，再一次计算和。然后对k也是使用递减，以后所有涉及到次数我们都可以用递减的方法，这样不用新定义变量。
标答：

class Solution {
static bool cmp(int a, int b) {return abs(a) > abs(b);
}
public:int largestSumAfterKNegations(vector<int>& A, int K) {sort(A.begin(), A.end(), cmp);       // 第一步for (int i = 0; i < A.size(); i++) { // 第二步if (A[i] < 0 && K > 0) {A[i] *= -1;K--;}}if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步int result = 0;for (int a : A) result += a;        // 第四步return result;}
};

实际运行出来还不如我们写的，不知道为什么。

思路：本题一开始想到的肯定是暴力方法，即遍历一圈的情况，时间复杂度O(n^2)。这里要注意实现细节，但是通不过，超时。这里重点理解rest==0的时候答案不唯一，如果rest等于0，说明有一段走不走都无所谓，因此可以从这一段的开头或者结尾走，都能走到，答案必定不唯一。不过本题设计测试用例的时候就只存在返回-1或者答案唯一的情况，不存在答案不唯一的情况，比如[1,1,1,1,1],[1,1,1,1,1]。

class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {for(int i=0;i<gas.size();i++){int rest=gas[i]-cost[i];//剩余油量int next=(i+1)%gas.size();while(rest>0&&next!=i){//还有油,而且没回来,rest如果等于0则答案不唯一rest=rest+gas[next]-cost[next];next=(next+1)%gas.size();}if(rest>=0&&next==i){//回来了return i;}}return -1;}
};

然后是贪心算法，这个实在想不到，直接看解答。首先是全局贪心方法，如果gas总和小于cost总和，一定跑不了一圈。计算rest[i]，从0开始累加，如果没有出现负数，则0就是起点。如果累加最小值为负数，则从非0节点出发，从后向前，看哪个节点可以把负数填满，即为出发点。时间复杂度O(n)。（说实话这个方法我还是没搞太懂）

class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int curSum = 0;int min = INT_MAX; // 从起点出发，油箱里的油量最小值for (int i = 0; i < gas.size(); i++) {//从0开始累加，先初始计算一下restint rest = gas[i] - cost[i];curSum += rest;if (curSum < min) {min = curSum;}}//算完后curSum为从0开始走完一圈后的油箱余量if (curSum < 0) return -1;  // 情况1,gas总和小于cost总和if (min >= 0) return 0;     // 情况2,如果最小油箱剩余最小值非负，则说明从0开始可以一圈走完，直接返回0// 情况3for (int i = gas.size() - 1; i > 0; i--) {//min小于0，从0走不到，开始考虑其他值int rest = gas[i] - cost[i];min += rest;if (min >= 0) {return i;}}return -1;}
};

详细分析一下，本解法的关键就是将油箱剩余最小值min记录，在从0走完一圈后，这个值就固定下来了，不会再变化了。但是这只是从0开始走的情况，如果从其他地方开始走，这个min的走一圈的变化幅度是固定不变的。当从0走一圈无法完成的时候，我们出发位置往前移动一格，这样就可以加上它的rest，从而判断能否走到。我们从n-1~1再反过来考虑，首先对n-1，min加上rest[n-1]，如果此时非负，则说明如果从n-1出发，走一圈的min不会有负数，故4能够完成，如果不行则继续往前考虑3，累加min，一直考虑到1结束（0最开始已经考虑过）。这个解法没有找出局部最优，因此不能完全认为是一种贪心算法，这也就是我们说贪心算法很多没有思路的原因。
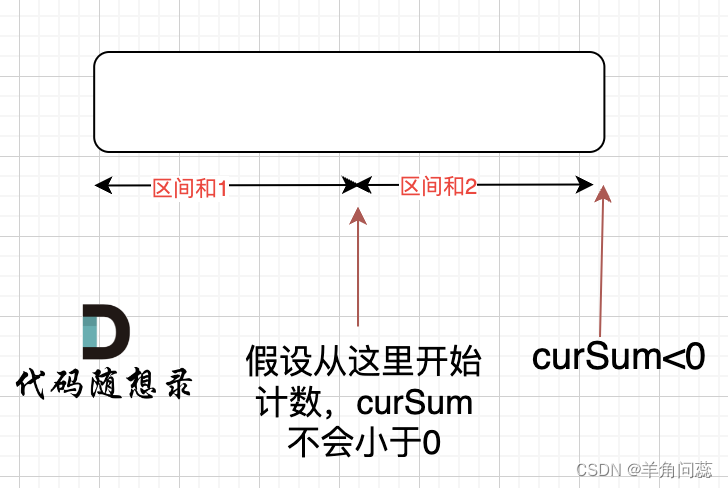
看解析还有贪心方法二：即rest和累加走一圈，小于0则不行，在累加到i的过程中，一旦遇到小于0，则说明前面的都不能作为开始，只能从i+1开始，即始终确保局部最优。这里有一个问题，那就是0~i有没有可能出现满足条件的起始？实际是不能的，因为在这个起始点前面的累加和必定小于0，则这时候直接从i+1开始考虑了，也不会漏掉情况。同时还要计算rest总和，总和必须非负，只要总和非负，而从start开始走到n-1也能保证中间没有油量为负的情况，则说明start必定满足，因为再往后走一圈的总和也非负了。时间复杂度O(n)。

代码如下：

class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int curSum=0;int start=0;int totalSum=0;for (int i = 0; i < gas.size(); i++) {//从0开始累加，先初始计算一下restint rest = gas[i] - cost[i];totalSum+=rest;curSum+=rest;if(curSum<0){start=i+1;curSum=0;}}if(totalSum<0) return -1;return start;}
};

思路：本题过于困难，想不到思路，直接看解答。本题关键是要对左边和右边分开考虑，先考虑右边分数大于左边的情况，首先所有孩子分一个，然后只要右边比左边分高，那么就给右边加一个，这时从左往右遍历；然后再考虑左边比右边分高的情况，这时取原本值和右边值加一的最大值，这时从右往左遍历。因为第一遍遍历的时候全是1，故右大于左直接加一就OK，而第二遍遍历的时候，candys数组已经发生了变化，可能原本左边就满足比右边大，这时就不能直接右加一，而是要先比较是不是本来就满足。时间复杂度O(n)。

class Solution {
public:int candy(vector<int>& ratings) {int n=ratings.size();int ans=0;vector<int> candys(n,1);//初始化糖果数组，每个孩子发一个for(int i=1;i<n;i++){if(ratings[i]>ratings[i-1]){candys[i]=candys[i-1]+1;}}for(int i=n-2;i>=0;i--){if(ratings[i]>ratings[i+1]){if(candys[i]<=candys[i+1]){candys[i]=candys[i+1]+1;}}}for(int i=0;i<n;i++){ans+=candys[i];}return ans;}
};

我写出的答案和标答略有区别，主要从右往左遍历的时候多用了个if，而没有用max，实际是一样的。