java算法day46 | 动态规划part08 ● 139.单词拆分 ● 关于多重背包，你该了解这些！ ● 背包问题总结篇！

139.单词拆分

在这里插入图片描述

完全背包问题，只不过装入背包时需要附加一个判断条件。

class Solution {public boolean wordBreak(String s, List<String> wordDict) {boolean[] dp=new boolean[s.length()+1];dp[0]=true;for(int j=1;j<=s.length();j++){for(int i=0;i<wordDict.size();i++){String word=wordDict.get(i);if(j>=word.length() && dp[j-word.length()] && word.equals(s.substring(j-word.length(),j))) {dp[j]=true;break;}}}return dp[s.length()];}
}

时间复杂度：O(n^3)，因为substring返回子串的副本是O(n)的复杂度（这里的n是substring的长度）
空间复杂度：O(n)

关于多重背包，你该了解这些！

对于多重背包，我在力扣上还没发现对应的题目，所以这里就做一下简单介绍，大家大概了解一下。

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

多重背包和01背包是非常像的，为什么和01背包像呢？

每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了。

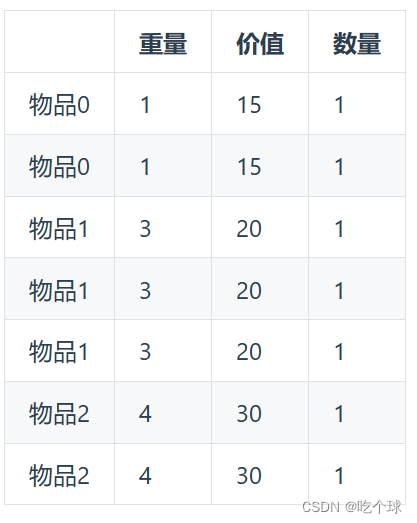
例如：

背包最大重量为10。

物品为：
在这里插入图片描述
问背包能背的物品最大价值是多少？

和如下情况有区别么？
在这里插入图片描述
练习题目：卡码网题目

import java.util.Scanner;
class multi_pack{public static void main(String [] args) {Scanner sc = new Scanner(System.in);/*** bagWeight:背包容量* n:物品种类*/int bagWeight, n;//获取用户输入数据，中间用空格隔开，回车键换行bagWeight = sc.nextInt();n = sc.nextInt();int[] weight = new int[n];int[] value = new int[n];int[] nums = new int[n];for (int i = 0; i < n; i++) weight[i] = sc.nextInt();for (int i = 0; i < n; i++) value[i] = sc.nextInt();for (int i = 0; i < n; i++) nums[i] = sc.nextInt();int[] dp = new int[bagWeight + 1];//先遍历物品再遍历背包，作为01背包处理for (int i = 0; i < n; i++) {for (int j = bagWeight; j >= weight[i]; j--) {//遍历每种物品的个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) {dp[j] = Math.max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}System.out.println(dp[bagWeight]);}
}

背包问题总结篇！

背包递推公式

问能否能装满背包（或者最多装多少）：
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
对应题目如下：
动态规划：416.分割等和子集
动态规划：1049.最后一块石头的重量 II
问装满背包有几种方法：dp[j] += dp[j - nums[i]] ，对应题目如下：
动态规划：494.目标和
动态规划：518. 零钱兑换 II
动态规划：377.组合总和Ⅳ
动态规划：70. 爬楼梯进阶版（完全背包）
问背包装满最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：
动态规划：474.一和零
问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
对应题目如下：
动态规划：322.零钱兑换
动态规划：279.完全平方数