1.训练集
使用Numpy数组存储数据集。

2.打印数组
打印两个数组的形状和数据。

3.初始化w,b
为了演示,w,b预设出接近最优解的值。w是一个一维数组,w个数对应特征个数。

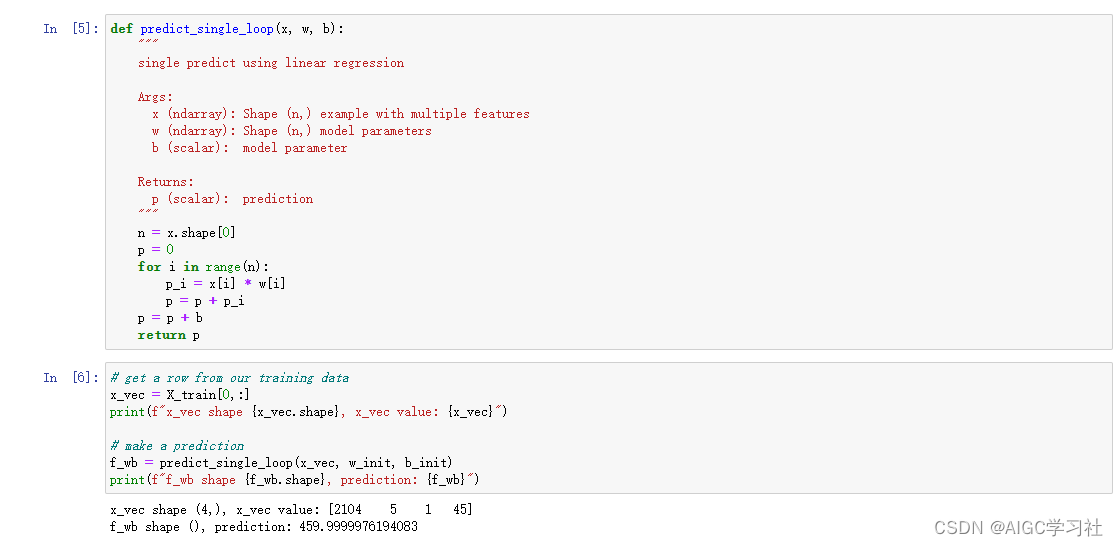
4.非向量化计算多元线性回归函数
使用for循环,计算每个w和x的乘积。
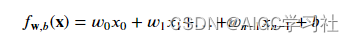
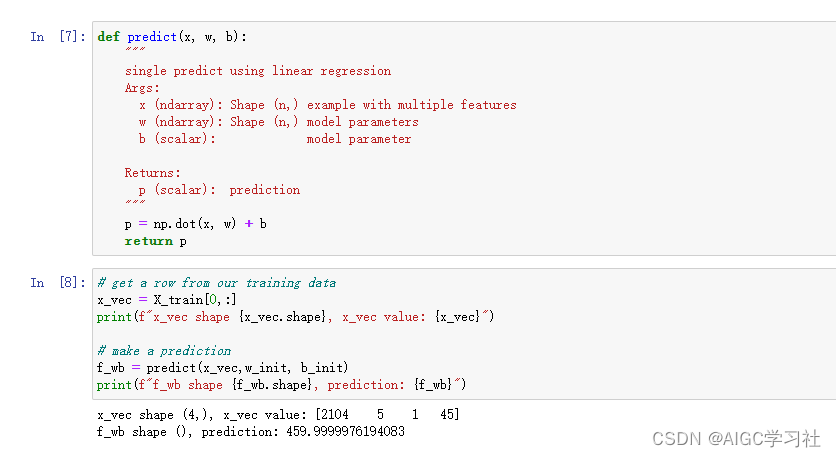
5.向量化计算多元线性回归函数
使用Numpy的dot方法,一行代码实现每个w和x的乘积。
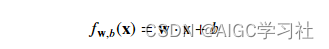
5.向量化计算多元线性回归的成本函数
每一组训练样本的预测值,都使用np.dot()+b。
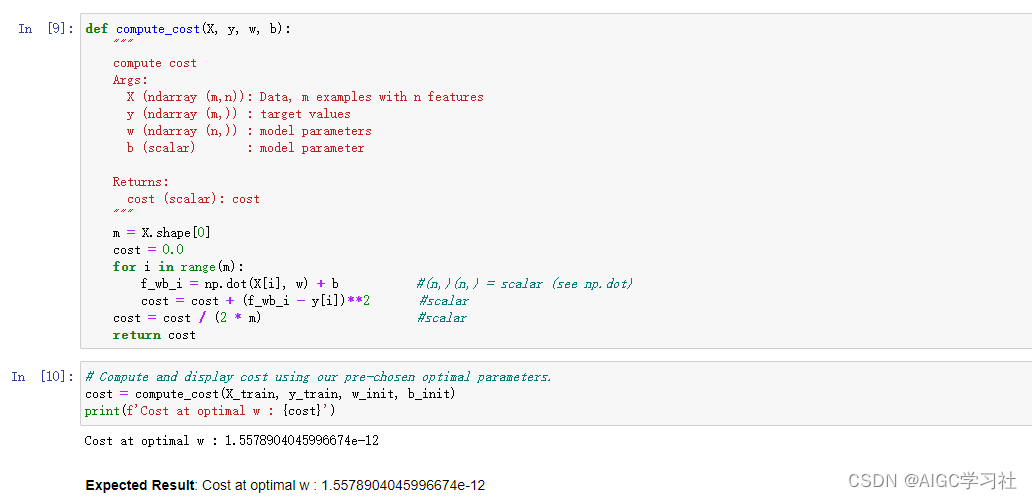
6.计算多元线性回归的成本函数的梯度
第一层循环,计算每组训练样本的误差。第二层循环,遍历并计算每组训练样本的n个特征。
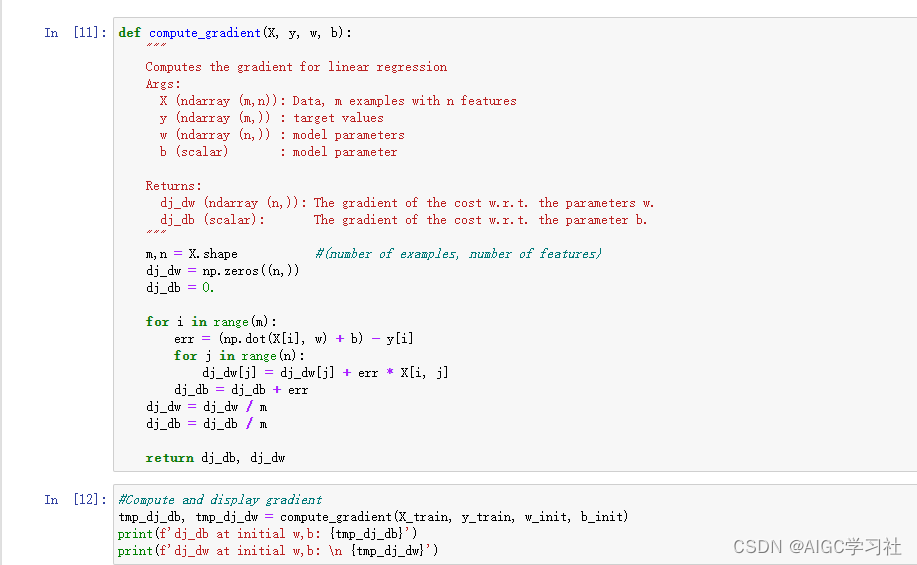
- 第二层循环有点绕,只需要记住,我们要计算多个w,有几个特征列,就要计算几个w。如果有4个特征列,则需要通过公式,分别计算并更新w1,w2,w3,w4。dj_dw数组保存的就是这4个w。dj_dw里最终保存的内容,是计算一次梯度后,w1,w2,w3,w4的值是多少。X[i,j]对应第i行训练样本里的第j个特征。
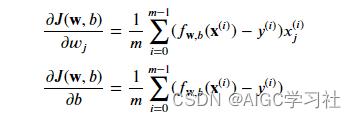
7.运行梯度下降函数
这里的w是向量化操作,w的第一个元素减去α乘以dj_dw的第一个元素,然后更新到w的第一个元素。
里面的计算可以形象化为: [w1 - (alpha * dj_dw[0]), w2 - (alpha * dj_dw2[1])…]
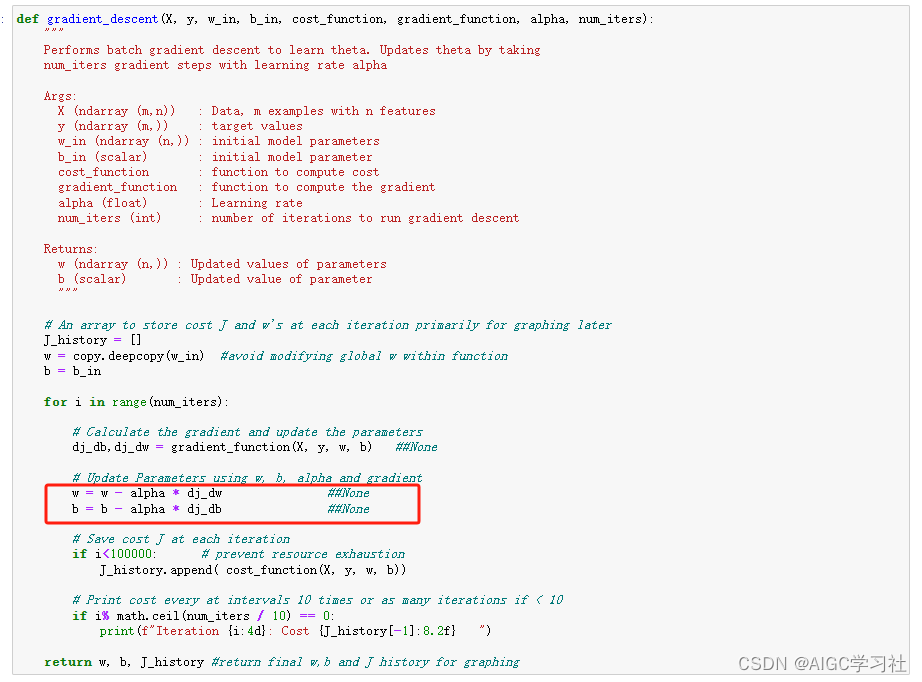
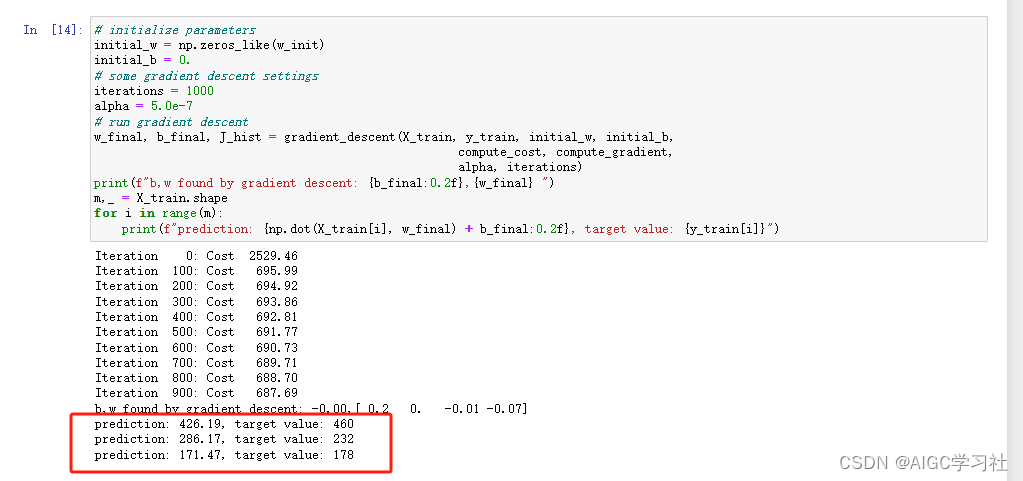
8.运行梯度下降
执行梯度下降计算出w,b,使用w,b,通过训练集计算预测,发现与训练集的真实数据误差较大。
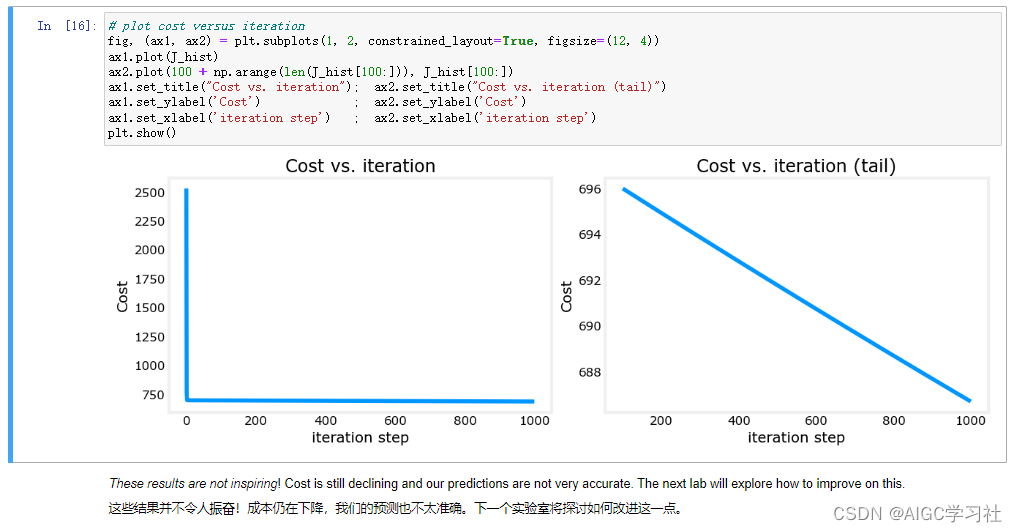
9.可视化迭代次数和成本函数
第一张图,迭代一开始,注意Y轴,成本函数的值就迅速降到750以下,。
第二张图细化了第一张图的直线部分,注意Y轴,迭代一开始,成本函数696开始缓慢下降,下降幅度变小。
















)


