✨✨ 欢迎大家来到贝蒂大讲堂✨✨
🎈🎈养成好习惯,先赞后看哦~🎈🎈
所属专栏:数据结构与算法
贝蒂的主页:Betty’s blog
1. 双向队列的定义
**双向队列(double‑ended queue)**是一种特殊的队列,它允许在队列的队尾与队头插入与删除元素。根据其定义,我们也可以理解为两个栈在栈底相连。
- 队尾入队

- 队首入队
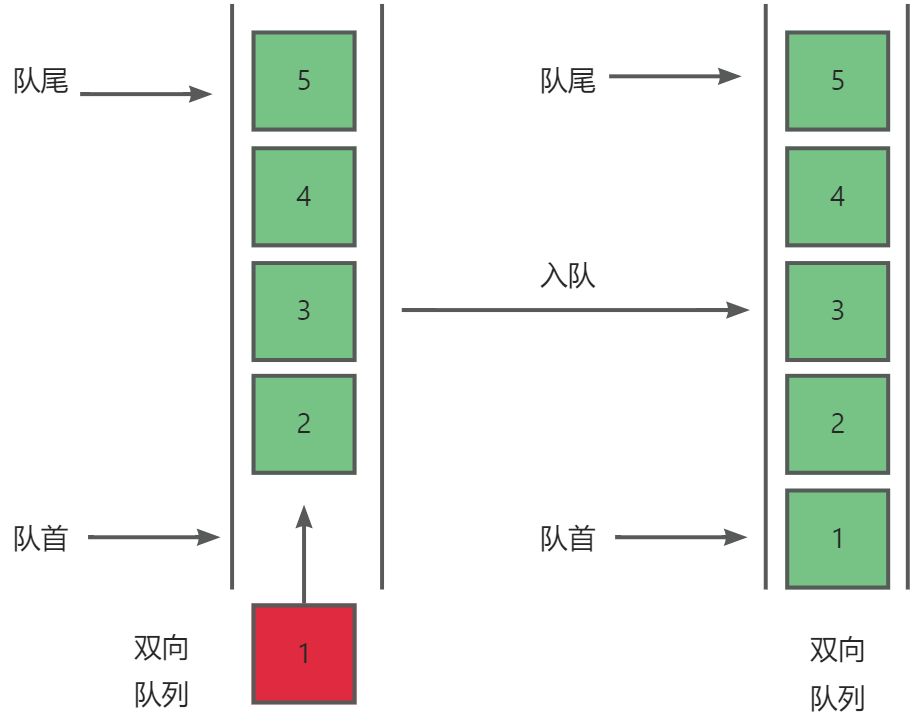
- 队尾出队
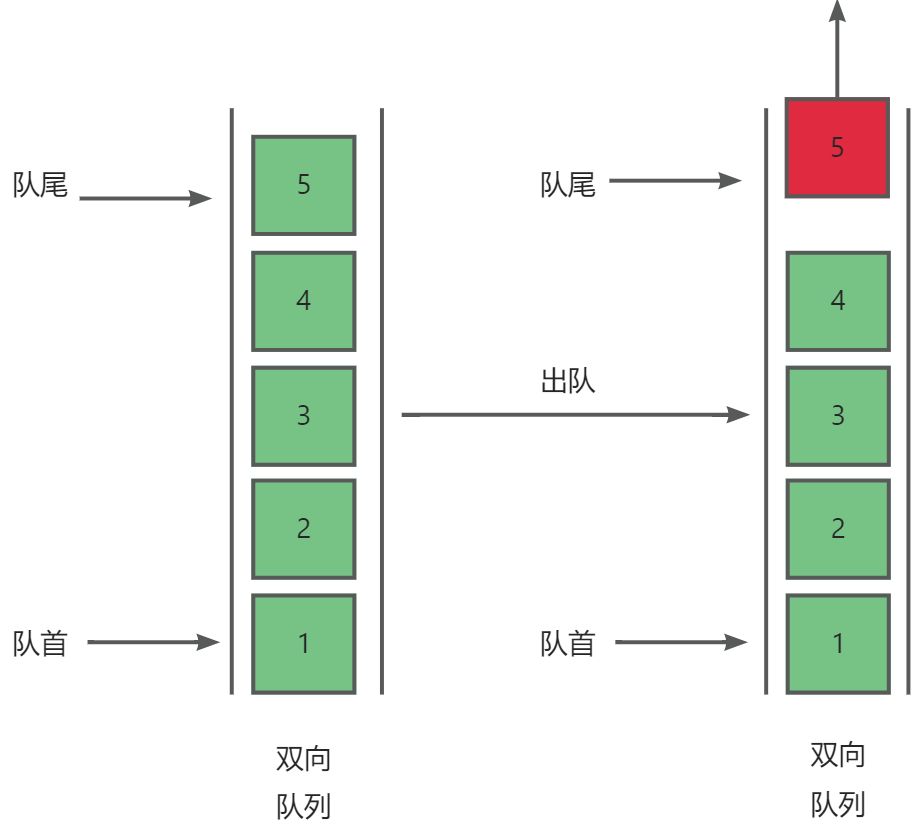
- 队尾出队

2. 双向队列的分类
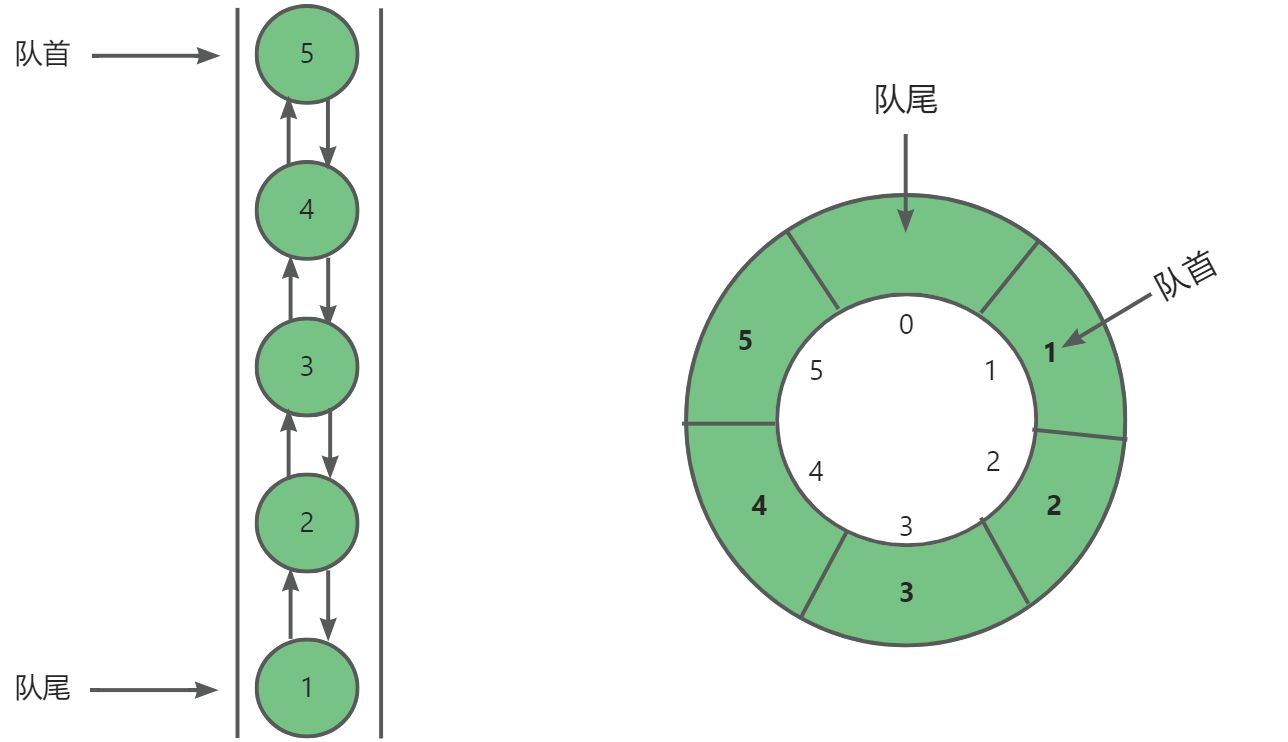
双向队列也是线性表的一种,所以也可以分别用链表与数组实现。基于链表实现:为了方便双向队列在尾部的插入与删除操作,所以我们选用双向链表。基于数组实现:与队列实现类似,需要用循环数组(原因参考队列实现)。
3. 双向队列的功能
- 队列的初始化。
- 判断队列是否为空。。
- 返回队头与队尾的元素。
- 返回队列的大小。
- 入队与出队。
- 打印队列的元素。
- 销毁队列。
4. 双向队列的声明
4.1. 链式队
双向队列与普通队列的声明区别就在于双向队列是基于双向链表的方式实现。
typedef int QDataType;
typedef struct DuListNode
{QDataType data;struct Node* prev;struct Node* next;
}DuListNode;typedef struct Deque
{size_t size;DuListNode* front;DuListNode* rear;
}Deque;
4.2. 循环队
循环队列的实现方式与普通队列差不多。
typedef int QDataType;
#define MAXSIZE 50 //定义元素的最大个数
typedef struct {QDataType *data;int front; //头指针int rear; //尾指针
}Deque;
5. 队列的初始化
5.1. 链式队
void DequeInit(Deque* d)//初始化
{assert(d);d->front = NULL;d->rear = NULL;d->size = 0;
}
5.2. 循环队
void DequeInit(Deque* d)//初始化
{d->data = (QDataType*)malloc(sizeof(QDataType )* MAXSIZE);if (d->data == NULL){perror("malloc fail:");return;}d->front = 0;d->rear = 0;
}
5.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:链式队空间是一个固定大小,空间复杂度为O(1)。而需要开辟整个队列的大小,空间复杂度为O(N)。
6. 判断队列是否为空
6.1. 链式队
bool DequeEmpty(Deque* d)//判断是否为空
{assert(d);return (d->front == NULL) && (d->rear == NULL);
}
6.2. 循环队
bool DequeEmpty(Deque* d)//判断是否为空
{assert(d);return d->front == d->rear;
}
6.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)。
7. 判断队列是否为满
7.1. 链式队
链式队并不需要判断。
7.2. 循环队
为什么要取模操作,可以参考一下上一篇普通队列的实现,同下。
bool DequeFull(Deque* d)//判断队列是否满
{assert(d);return (d->rear + 1) % MAXSIZE == d->front;
}
8. 返回队头与队尾的元素
8.1. 链式队
QDataType DequeFront(Deque* d)//获取队头元素
{assert(d);assert(!DequeEmpty(d));return d->front->data;
}
QDataType DequeBack(Deque* d)//获取队尾元素
{assert(d);assert(!DequeEmpty(d));return d->rear->data;
}
8.2. 循环队
QDataType DequeFront(Deque* d)//获取队头元素
{assert(d);assert(!DequeEmpty(d));return d->data[d->front];
}
QDataType DequeBack(Deque* d)//获取队尾元素
{assert(d);assert(!DequeEmpty(d));return d->data[(d->rear-1+MAXSIZE)%MAXSIZE];
}
8.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
9. 返回队列的大小
9.1. 链式队
size_t DequeSize(Deque* d)//队列长度
{return d->size;
}
9.2. 循环队
size_t DequeSize(Deque* d)//获取队列长度
{assert(d);return (d->rear - d->front + MAXSIZE) % MAXSIZE;
}
9.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
10. 入队
10.1. 链式队
10.1.1. 队头入队
void DequeFrontPush(Deque* d, QDataType x)//队首入队
{assert(d);DuListNode* newnode = (DuListNode*)malloc(sizeof(DuListNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;if (d->front == NULL){d->front = d->rear = newnode;}else{d->front->prev = newnode;newnode->next = d->front;d->front = newnode;}d->size++;
}
10.1.2. 队尾入队
void DequeRearPush(Deque* d, QDataType x)//队尾入队
{assert(d);DuListNode* newnode = (DuListNode*)malloc(sizeof(DuListNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;if (d->front == NULL){d->front = d->rear = newnode;}else{d->rear->next = newnode;newnode->prev = d->rear;d->rear = newnode;}d->size++;
}
10.2. 循环队
入队需要提前判断队列是否为满。
10.2.1. 队头入队
void DequeFrontPush(Deque* d, QDataType x)//队首入队
{assert(d);if (DequeFull(d)){printf("队列已满\n");return;}d->data[(d->front - 1 + MAXSIZE) % MAXSIZE]=x;d->front = (d->front - 1 + MAXSIZE) % MAXSIZE;
}
10.2.2. 队尾入队
void DequeRearPush(Deque* d, QDataType x)//队尾入队
{assert(d);if (DequeFull(d)){printf("队列已满\n");return;}d->data[d->rear] = x;d->rear = (d->rear + 1) % MAXSIZE;
}
10.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
11. 出队
11.1. 链式队
出队需要提前判断队列是否为空。
11.1.1. 队头出队
void DequeFrontPop(Deque* d)//队首出队
{assert(d);assert(!DequeEmpty(d));//1.只有一个结点if (d->front == d->rear){free(d->front);d->front = d->rear = NULL;}//2.有多个结点else{DuListNode* next = d->front->next;next->prev = NULL;d->front->next = NULL;free(d->front);d->front = next;}d->size--;
}
11.1.2. 队尾出队
void DequeRearPop(Deque* d)//队尾出队
{assert(d);assert(!DequeEmpty(d));//1.只有一个结点if (d->front == d->rear){free(d->front);d->front = d->rear = NULL;}else{DuListNode* prev = d->rear->prev;prev->next = NULL;d->rear->prev = NULL;free(d->rear);d->rear = prev;}d->size--;
}
11.2. 循环队
11.2.1. 队头出队
void DequeFrontPop(Deque* d)//队首出队
{assert(d);assert(!DequeEmpty(d));d->front = (d->front + 1) % MAXSIZE;
}
11.2.2. 队尾出队
void DequeRearPop(Deque* d)//队尾出队
{assert(d);assert(!DequeEmpty(d));d->rear = (d->rear - 1+MAXSIZE) % MAXSIZE;
}
11.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
12. 打印队列元素
12.1. 链式队
void DequePrint(Deque* d)//打印队列元素
{assert(d);DuListNode* cur = d->front;DuListNode* tail = d->rear;printf("队头:");while (cur != tail->next){printf("%d<=>", cur->data);cur = cur->next;}printf("队尾\n");
}
12.2. 循环队
void DequePrint(Deque* d)//打印队列元素
{assert(d);int cur = d->front;printf("队头->");while (cur != d->rear){printf("%d->", d->data[cur]);cur = (cur + 1) % MAXSIZE;}printf("队尾\n");}
12.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列都需要遍历这个队列,所以时间复杂度为O(N)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
13. 销毁队列
13.1. 链式队
void DequeDestroy(Deque* d)//销毁队列
{assert(d);DuListNode* cur = d->front;while (cur){DuListNode* del = cur;cur = cur->next;free(del);del = NULL;}d->front = d->rear = NULL;
}
13.2. 循环队
void DequeDestroy(Deque* d)//销毁队列
{assert(d);free(d->data);d->data = NULL;d->front = d->rear = 0;
}
13.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
14. 对比与应用
14.1. 对比
双向队列的两种实现方式的效果与普通队列实现差不多,这里就不在一一赘述。
14.2. 应用
双向队列兼备队列与栈的性质,所以可以应用于这两种数据结构的所有应用场景。
此外它应用于撤销的一种情景:通常情况下,撤销是以栈的方式实现,当我们每次更改时就入栈,撤销就出栈。但是我们知道系统给与栈的空间是有限的,我们不可能一直入栈。当入栈超过一个限度时,我们就用过删除栈底的数据,这时栈这个数据结构就无法满足需求。所以这时我们可以使用双向队列来实现。
15. 完整代码
15.1. 链式队
15.1.1. Deque.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int QDataType;
typedef struct DuListNode
{QDataType data;struct Node* prev;struct Node* next;
}DuListNode;typedef struct Deque
{size_t size;DuListNode* front;DuListNode* rear;
}Deque;
void DequeInit(Deque* d);//初始化
bool DequeEmpty(Deque* d);//判断是否为空
QDataType DequeFront(Deque* d);//获取队头元素
QDataType DequeBack(Deque* d);//获取队尾元素
size_t DequeSize(Deque* d);//获取队列长度
void DequeFrontPush(Deque* d, QDataType x);//队首入队
void DequeRearPush(Deque* d, QDataType x);//队尾入队
void DequeFrontPop(Deque* d);//队首出队
void DequeRearPop(Deque* d);//队尾出队
void DequePrint(Deque* d);//打印队列元素
void DequeDestroy(Deque* d);//销毁队列
15.1.2. Deque.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Deque.h"
void DequeInit(Deque* d)//初始化
{assert(d);d->front = NULL;d->rear = NULL;d->size = 0;
}
bool DequeEmpty(Deque* d)//判断是否为空
{assert(d);return (d->front == NULL) && (d->rear == NULL);
}
QDataType DequeFront(Deque* d)//获取队头元素
{assert(d);assert(!DequeEmpty(d));return d->front->data;
}
QDataType DequeBack(Deque* d)//获取队尾元素
{assert(d);assert(!DequeEmpty(d));return d->rear->data;
}
size_t DequeSize(Deque* d)//队列长度
{return d->size;
}
void DequeFrontPush(Deque* d, QDataType x)//队首入队
{assert(d);DuListNode* newnode = (DuListNode*)malloc(sizeof(DuListNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;if (d->front == NULL){d->front = d->rear = newnode;}else{d->front->prev = newnode;newnode->next = d->front;d->front = newnode;}d->size++;
}
void DequeRearPush(Deque* d, QDataType x)//队尾入队
{assert(d);DuListNode* newnode = (DuListNode*)malloc(sizeof(DuListNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;if (d->front == NULL){d->front = d->rear = newnode;}else{d->rear->next = newnode;newnode->prev = d->rear;d->rear = newnode;}d->size++;
}
void DequeFrontPop(Deque* d)//队首出队
{assert(d);assert(!DequeEmpty(d));//1.只有一个结点if (d->front == d->rear){free(d->front);d->front = d->rear = NULL;}//2.有多个结点else{DuListNode* next = d->front->next;next->prev = NULL;d->front->next = NULL;free(d->front);d->front = next;}d->size--;
}
void DequeRearPop(Deque* d)//队尾出队
{assert(d);assert(!DequeEmpty(d));//1.只有一个结点if (d->front == d->rear){free(d->front);d->front = d->rear = NULL;}else{DuListNode* prev = d->rear->prev;prev->next = NULL;d->rear->prev = NULL;free(d->rear);d->rear = prev;}d->size--;
}
void DequePrint(Deque* d)//打印队列元素
{assert(d);DuListNode* cur = d->front;DuListNode* tail = d->rear;printf("队头:");while (cur != tail->next){printf("%d<=>", cur->data);cur = cur->next;}printf("队尾\n");
}
void DequeDestroy(Deque* d)//销毁队列
{assert(d);DuListNode* cur = d->front;while (cur){DuListNode* del = cur;cur = cur->next;free(del);del = NULL;}d->front = d->rear = NULL;
}
15.2. 循环队
15.2.1. Deque.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int QDataType;
#define MAXSIZE 50 //定义元素的最大个数
typedef struct {QDataType *data;int front; //头指针int rear; //尾指针
}Deque;void DequeInit(Deque* d);//初始化
bool DequeEmpty(Deque* d);//判断是否为空
bool DequeFull(Deque* d);//判断队列是否满
QDataType DequeFront(Deque* d);//获取队头元素
QDataType DequeBack(Deque* d);//获取队尾元素
size_t DequeSize(Deque* d);//获取队列长度
void DequeFrontPush(Deque* d, QDataType x);//队首入队
void DequeRearPush(Deque* d, QDataType x);//队尾入队
void DequeFrontPop(Deque* d);//队首出队
void DequeRearPop(Deque* d);//队尾出队
void DequePrint(Deque* d);//打印队列元素
void DequeDestroy(Deque* d);//销毁队列
15.2.2. Deque.c
void DequeInit(Deque* d)//初始化
{d->data = (QDataType*)malloc(sizeof(QDataType )* MAXSIZE);if (d->data == NULL){perror("malloc fail:");return;}d->front = 0;d->rear = 0;
}
bool DequeEmpty(Deque* d)//判断是否为空
{assert(d);return d->front == d->rear;
}
bool DequeFull(Deque* d)//判断队列是否满
{assert(d);return (d->rear + 1) % MAXSIZE == d->front;
}
QDataType DequeFront(Deque* d)//获取队头元素
{assert(d);assert(!DequeEmpty(d));return d->data[d->front];
}
QDataType DequeBack(Deque* d)//获取队尾元素
{assert(d);assert(!DequeEmpty(d));return d->data[(d->rear-1+MAXSIZE)%MAXSIZE];
}
size_t DequeSize(Deque* d)//获取队列长度
{assert(d);return (d->rear - d->front + MAXSIZE) % MAXSIZE;
}
void DequeFrontPush(Deque* d, QDataType x)//队首入队
{assert(d);if (DequeFull(d)){printf("队列已满\n");return;}d->data[(d->front - 1 + MAXSIZE) % MAXSIZE]=x;d->front = (d->front - 1 + MAXSIZE) % MAXSIZE;
}
void DequeRearPush(Deque* d, QDataType x)//队尾入队
{assert(d);if (DequeFull(d)){printf("队列已满\n");return;}d->data[d->rear] = x;d->rear = (d->rear + 1) % MAXSIZE;
}
void DequeFrontPop(Deque* d)//队首出队
{assert(d);assert(!DequeEmpty(d));d->front = (d->front + 1) % MAXSIZE;
}
void DequeRearPop(Deque* d)//队尾出队
{assert(d);assert(!DequeEmpty(d));d->rear = (d->rear - 1+MAXSIZE) % MAXSIZE;
}
void DequePrint(Deque* d)//打印队列元素
{assert(d);int cur = d->front;printf("队头->");while (cur != d->rear){printf("%d->", d->data[cur]);cur = (cur + 1) % MAXSIZE;}printf("队尾\n");}
void DequeDestroy(Deque* d)//销毁队列
{assert(d);free(d->data);d->data = NULL;d->front = d->rear = 0;
}





-2-CSS 盒子模型)












LoRa(sx1278))

 | 一次调用,两次返回)