---

2810. 故障键盘

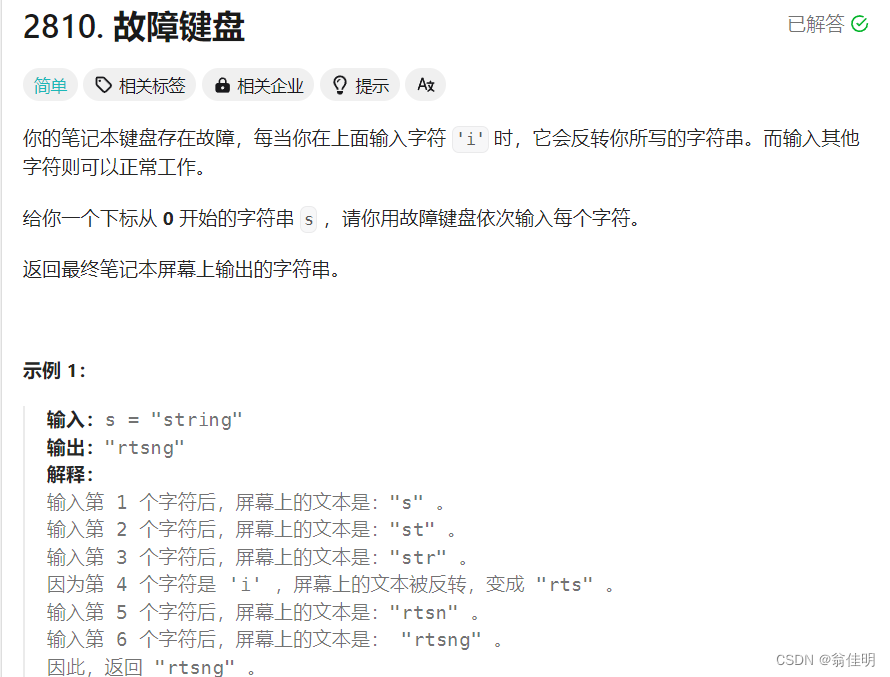
思路一：模拟

• 用StringBuilder来拼贴字符
• 遍历字符串，如果遇到i,对拼贴好的进行逆置
• 否则，进行拼贴
• 最终返回字符串类型

代码：

   // 2810. 故障键盘public String finalString(String s) {StringBuilder sb = new StringBuilder();for (char x : s.toCharArray()) {if (x == 'i') {sb.reverse();} else {sb.append(x);}}return sb.toString();}

思路二：双端队列

• 调用双端队列
• 如果遇到i,需要进行逆置，相当于进行头插法，改变标记
• 没遇到i,并且标记为真，进行尾插法
• 最后检查是否需要逆置

代码：

    public String finalString(String s) {// 双端队列Deque<Character> deque = new ArrayDeque<>();StringBuilder sb = new StringBuilder();boolean flg = true;for (char x : s.toCharArray()) {if (x == 'i') {flg = !flg;//碰到i,进行逆置//再次碰到i,反过耒} else if (flg) {//如果为真，添加到队尾deque.addLast(x);}else {//x不等于i,并且由于前一个是i,发生逆转// 相当于添加到队头deque.addFirst(x);}}for (char c:deque) {sb.append(c);}if (!flg){sb.reverse();}return sb.toString();}

点击移步博客主页，欢迎光临~