---

1.背景

2021年，H Peraza-Vázquez等人受到跳蛛狩猎行为启发，提出了跳蛛优化算法（Jumping Spider Optimization Algorithm，JSOA）。

2.算法原理

2.1算法思想

JSOA模拟了跳蛛的捕猎行为，主要包括跳蛛捕猎时的迫害、跳向猎物、搜索行为，并通过信息素来优化位置不佳的跳蛛。

2.2算法过程

迫害：

当跳蛛跳跃距离不够捕捉猎物时，它会通过一些隐蔽的移动靠近猎物：
$${\vec{x}}_i(g+1)=\frac{1}{2}({\vec{x}}_i(g)-{\vec{x}}_r(g))\text{\hspace{1em}(1)}$$
其中，xr为不等于xi的随机跳蛛。

跳向猎物：

跳蛛扑向猎物的行为可以表示为初速度为V0，与水平夹角为φ 的 抛 物 线 运 动。该抛物线运动水平方向速度与竖直方向速度为：
$$\begin{array}{rl}& {\vec{x}}_i=V_0\cos (\alpha )t\vec{i}\\ & {\vec{y}}_i=\left(V_0\sin (\alpha )t-\frac{1}{2}g{t}^2\right)\vec{j}\end{array}\text{\hspace{1em}(2)}$$
当时间间隔为1时，可以得到：
$$y=x\tan (\alpha )-\frac{g{x}^2}{2V_0^2{\cos }^2(\alpha )}\text{\hspace{1em}(3)}$$
跳向猎物过程可以表述为：
$$\begin{array}{rl}& {\vec{x}}_i(g+1)={\vec{x}}_i(g)\tan (\alpha )-\frac{g{\vec{x}}_i^2(g)}{2V_0^2{\cos }^2(\alpha )}\\ & \alpha =\frac{\varphi \pi }{180}\end{array}\text{\hspace{1em}(4)}$$

搜索猎物:

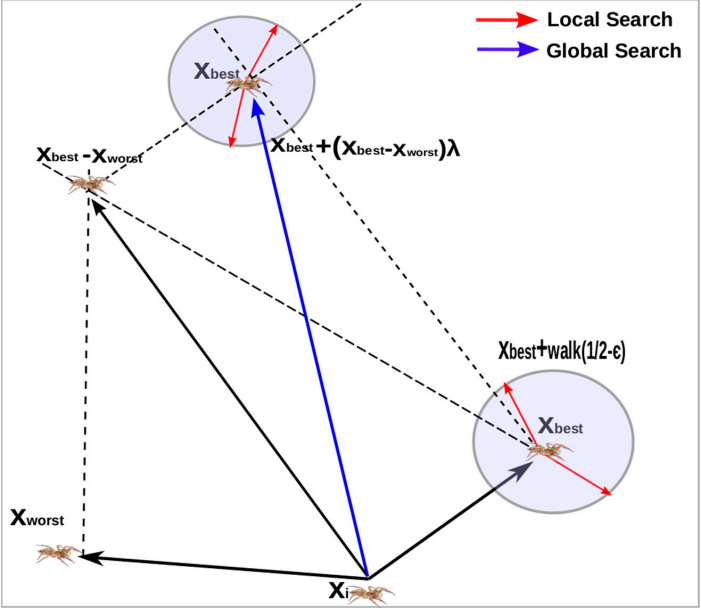
跳蛛在周围环境进行随机搜索以找到猎物，算法提供了局部搜索和全局搜索。局部搜索表述为：
$${\vec{x}}_i(g+1)={\vec{x}}_{\mathrm{best}}(g)+WALK\left(\frac{1}{2}-\epsilon \right)\text{\hspace{1em}(5)}$$
全局搜索表述为：
$${\vec{x}}_i(g+1)={\vec{x}}_{\mathrm{best}}(g)+({\vec{x}}_{\mathrm{best}}(g)-{\vec{x}}_{\mathrm{worst}}(g))\lambda \text{\hspace{1em}(6)}$$

信息素:

第i只跳蛛信息素为：
$$pheromone\left(i\right)=\frac{Fitnes{s}_{\max }-Fitness\left(i\right)}{Fitnes{s}_{\max }-Fitnes{s}_{\min }}\text{\hspace{1em}(7)}$$
当信息素小于或等于0.3时:
$${\vec{x}}_i(g)={\vec{x}}_{\text{best}}(g)+\frac{1}{2}({\vec{x}}_{r1}(g)-(-1{)}^{\sigma }{\vec{x}}_{r2}(g))$$

伪代码：

3.结果展示

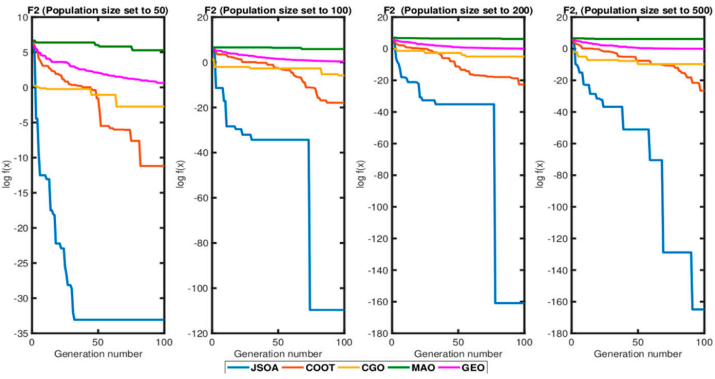
4.参考文献

[1] Peraza-Vázquez H, Peña-Delgado A, Ranjan P, et al. A bio-inspired method for mathematical optimization inspired by arachnida salticidade[J]. Mathematics, 2021, 10(1): 102.