一、实验目的
1.加深学生对分治法算法设计方法的基本思想、基本步骤、基本方法的理解与掌握;
2.提高学生利用课堂所学知识解决实际问题的能力;
3.提高学生综合应用所学知识解决实际问题的能力。
二、实验任务
1、 编写一个生命游戏:
规则如下:(或者网上找到更详细的规则)
一个人可以有8个邻居;
一个人若只有一个邻居,在下一代会孤独的死去;
若有2或3个邻居,在下一代依然活着;
若有4个或以上邻居,在下一代会因拥挤而死;
死去的人若有3个邻居,在下一代会复活;
所有的死去或复活都在下一代变化时同时发生。
2、 带锁的门:
在走廊上有n个带锁的门,从1到n依次编号。最初所有的门都是关着的。我们从门前经过n次,每次都从1号门开始。在第i次经过时(i = 1,2,…, n)我们改变i的整数倍号锁的状态;如果门是关的,就打开它;如果门是打开的,就关上它。在最后一次经过后,哪些门是打开的,哪些门是关上的?有多少打开的门?
3、排序算法
目前已知有几十种排序算法,请查找资料,并尽可能多地实现多种排序算法,并分析算法的时间复杂度。比较各种算法的优劣。
4、三壶谜题:
有一个充满水的8品脱的水壶和两个空水壶(容积分别是5品脱和3品脱)。通过将水壶完全倒满水和将水壶的水完全倒空这两种方式,在其中的一个水壶中得到4品脱的水。
5、交替放置的碟子
我们有数量为2n的一排碟子,n黑n白交替放置:黑,白,黑,白…
现在要把黑碟子都放在右边,白碟子都放在左边,但只允许通过互换相邻碟子的位置来实现。为该谜题写个算法,并确定该算法需要执行的换位次数。
三、实验设备及编程开发工具
实验设备:Win10 电脑
开发工具:Microsoft Visual C++
四、实验过程设计(算法设计过程)
(一)、生命游戏
1、算法分析:
生命游戏的规则可简化如下:
1.邻居个数为0,1,4,5,6,7,8时则该细胞下次的状态为死亡。
2.邻居个数为2时,则该细胞下次状态为复活。
3.邻居个数为3时,则该细胞下次状态为稳定,运行结果为生成细胞存活的状态图。
4.最初细胞默认都是死亡状态,活细胞需要自己设定生成。
2、代码实现:
#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <conio.h>
#include <iostream>
#define ROWLEN 10//二维空间行数;
#define COLLEN 10//二维空间列数;
#define DEAD 0 //死细胞;
#define ALIVE 1 //活细胞;
using namespace std;
int cell[ROWLEN][COLLEN];//当前生命细胞的状态;
int celltemp[ROWLEN][COLLEN];//用于判断当前细胞的下一个状态
void initcell() {int row,col;for(row=0; row<ROWLEN; row++) {for(col=0; col<COLLEN; col++) {cell[row][col]=DEAD;}}printf("输入一组活细胞的坐标位置,输入(-1,1)结束\n");while(1) {printf("输入一个活细胞的坐标位置: ");cin>>row>>col;if(0<=row&&row<ROWLEN&&0<=col&&col<COLLEN) {cell[row][col]=ALIVE;} else if(row==-1||col==-1) {break;} else {printf("输入坐标超过范围。\n");}}}
int LinSum(int row,int col) {int count=0,c,r;for(r=row-1; r<=row+1; r++) {for(c=col-1; c<=col+1; c++) {if(r<0||r>=ROWLEN||c<0||c>=COLLEN) {continue;}if(cell[r][c]==ALIVE) {count++;}}}if(cell[row][col]==ALIVE) {count--;}return count;
}
void OutCell() {int row,col;printf("\n细胞状态\n");for(col=0; col<COLLEN-1; col++) {}cout<<endl;for(row=0; row<ROWLEN; row++) {for(col=0; col<COLLEN; col++) {switch(cell[row][col]) {case ALIVE:printf("●");//活细胞;break;case DEAD:printf("○");//死细胞;break;default:;}}printf("\n");}
void cellfun() {int row,col,sum;int count=0;for(row=0; row<ROWLEN; row++) {for(col=0; col<COLLEN; col++) {switch(LinSum(row,col)) { //四周活细胞适量;case 2:celltemp[row][col]=cell[row][col];//保持细胞原样;break;case 3:celltemp[row][col]=ALIVE;//复活;break;default://死了;celltemp[row][col]=DEAD;}}}for(row=0; row<ROWLEN; row++) {for(col=0; col<COLLEN; col++) {cell[row][col]=celltemp[row][col];}}for(row=0; row<ROWLEN; row++) {for(col=0; col<COLLEN; col++) {if(cell[row][col]==ALIVE) { //如果是活细胞;count++;//累计或细胞数量;}}}sum=count;OutCell() ;//显示当前细胞状态;printf("当前状态下,一共有%d个活细胞。\n",sum);
}
int main() {char again;printf("生命游戏!\n") ;initcell(); //初始化OutCell(); //输出初始细胞状态;printf("按任意键开始游戏,进行细胞转换。\n");getch() ;
S1:cellfun();
S2:printf("\n继续生成下一次细胞状态(y/n)?");fflush(stdin);cin>>again;if(again=='y'||again=='Y') {goto S1;} else if(again=='n'||again=='N') {goto S3;} else {printf("输入错误,请重新输入!\n");goto S2;}
S3:printf("游戏结束!\n");return 0;
}生命游戏
1、实验结果
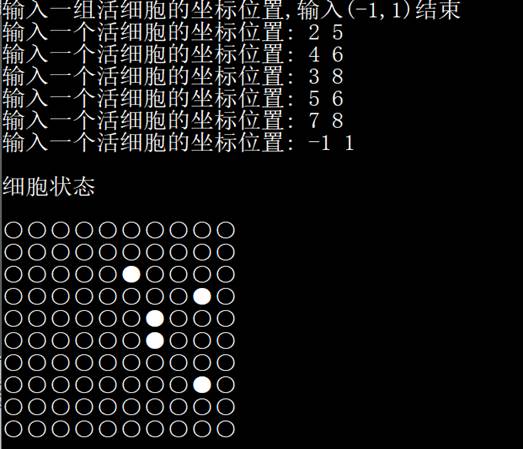
2、算法复杂度分析
时间复杂度:O(n^2)
(二)、带锁的门
1、算法分析:
从1-n的所有门,要经过n次:经过K次,若k(k<=n)可分解为i*j(i!=j),则第k个门一定会有偶数次开关门的变化,则最后门的状态还是关闭。如k = 18,可以分解成1x18,2x9,3x6,则第1次,2次,3次,6次,9次,18次经过第18号门,均会变化开关门的状态,原来是关门,经过偶数次变化,最终状态还是关门;若k为完全平方数,如1、4、9、16,则第k个门只会有奇数次变化。如k=4,只有1、2、4次经过会变化状态,故最后门是开的。按照如上的分析,我们只需要判断1-n个门中有多少个完全平方数,即可确定门开着的数目。
2、代码实现:
#include <stdio.h>
#define N 100
int main()
{
int L[N];
int i,j,k;
int n;
printf("输入门的总数,要求小于100:");
while(1)
{scanf("%d",&n);if(n<0||n>100)printf("输入错误,请重新输入");else break;
}
for(i=0;i<n;i++)L[i]=0;
for(j=1;j<=n;j++)
for(k=1;k<=n;k++)
if(k%j==0)
L[k-1]=(L[k-1]+1)%2;
for(i=0;i<n;i++)
{
if(L[i]==1)
printf("第%d号门开着\n",i+1);
}
printf("\n");
return 0;
}带锁的门
1、实验结果

2、算法复杂度分析
时间复杂度:O(n^2)
(三)、排序算法
1、冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法描述
a、比较相邻的元素。如果第一个比第二个大,就交换它们两个;
b、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
c、针对所有的元素重复以上的步骤,除了最后一个;
d、重复步骤1~3,直到排序完成。

2、快速排序
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。
**具体算法描述如下:**从数列中挑出一个元素,称为 “基准”(pivot);重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。

3、 归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
算法描述
a、把长度为n的输入序列分成两个长度为n/2的子序列;
b、对这两个子序列分别采用归并排序;
c、将两个排序好的子序列合并成一个最终的排序序列。

4、 计数排序
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
算法描述
找出待排序的数组中最大和最小的元素;统计数组中每个值为i的元素出现的次数,存入数组C的第i项;对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。

(四)、三壶谜题
1、算法分析:
可以把每次三个水壶中水量设成一组状态,比如初始状态为008,对应第一个水壶0品脱水,第二个水壶0品脱水,第三个水壶8品脱水。对题目的状态空间图进行广度优先遍历。当表示状态的数字中出现4时,即求出答案。
(1)打印倒水的过程,需要声明一个前置状态保存当前状态由哪个状态转换而来,然后就可以回溯到初始状态,打印出倒水过程。
(2)声明一个map表,保存已有的状态,对已有的状态就不再向下继续遍历。
(3)因为是广度优先遍历,所以第一次得到的答案所需的倒水次数最少,即为最优解。
2、代码实现:
#include <iostream>
#include <vector>
#include <map>
#define MaxFirst 3
#define MaxSecond 5
#define MaxThird 8
using namespace std;
class State
{
public:int second;int num[3];State* preState;static map<int,int> mapping;
public:State(int first,int second,int third){num[0]=first;num[1]=second;num[2]=third; }void init(){ mapping[0]=MaxFirst;mapping[1]=MaxSecond;mapping[2]=MaxThird;}bool canPour(int from,int to)//判断是否可以从from水壶中倒水到to水壶中{if(num[from]==0){return false;}if(num[to]==mapping[to]){return false;}else {return true;}}void pour(int from,int to)//倒水过程{if(num[from]+num[to]>mapping[to]){num[from]=num[from]-(mapping[to]-num[to]);num[to]=mapping[to];}else{num[to]=num[to]+num[from];num[from]=0;}}};
map<int,int> State::mapping;
int main()
{map<int,int> states;State *start=new State(0,0,8);start->init();State *state=start;State *endState=new State(8,8,8); //只有获得解endState才会改变,赋值全为8为了方便判断是否获得最终解vector<State> action; //保存所有状态对象action.push_back(*start); //把初始状态先加入队列中int n=0;do{for(int i=0;i<3;i++) //双层循环为从i水壶中倒水入j水壶中{for(int j=0;j<3;j++){if(i!=j){if(state->canPour(i,j)){state->pour(i,j);if(states[state->num[0]*100+state->num[1]*10+state->num[2]]==0)//如果该状态不在hash表中,即为第一次出现该状态{states[state->num[0]*100+state->num[1]*10+state->num[2]]++;(state->preState)=new State(action[n]);action.push_back(*state);if(state->num[0]==4||state->num[1]==4||state->num[2]==4)//获得解{endState=state;i=4;break; }}}}*state=action[n];} }n++;}while(endState->num[0]==8&&endState->num[1]==8&& n<action.size());cout<<endState->num[0]<<" "<<endState->num[1]<<" "<<endState->num[2]<<endl;state=endState;do{state=state->preState;cout<<state->num[0]<<" "<<state->num[1]<<" "<<state->num[2]<<endl; }while(state->num[2]!=8);return 0;
}三壶谜题
1、实验结果

2、算法复杂度分析
时间复杂度:O(n^2)
(五)、交替放置的碟子
1、算法分析:
将问题进行转化:用1表示黑碟子,0表示白碟子,那么目前的顺序是:1010…1010,结果要求1均放在右边,0放在左边。分析题意,算法思路符合冒泡排序算法:对于2n个碟子,可以使用n次迭代完成,交换的次数为:n+(n-1)+…+2+1,即n(n+1)/2。
2、代码实现:
#include <stdio.h>
#include <stdlib.h>
int main()
{int n,num=0;printf("输入碟子的总数量:");scanf("%d",&n);int sum[100];// 将所有碟子存放在一个数组里,设白碟子值为1,黑碟子值为2,//初始排序为:21212121……//换位后排序为 11112222……for(int i=0;i<=(n-2)/2;i++){sum[2*i]=2;sum[2*i+1]=1;}printf("碟子的初始状态如下:\n");//输出碟子的初始排序 for(i=0;i<n;i++){printf(sum[i]+" ");if(sum[i]==1){printf("白 ");}else{printf("黑 ");}}printf("\n");//进行排序for(i=0;i<n-1;i++){for(int j=0;j<(n-1-i);j++){if(sum[j+1]<sum[j]){int t=sum[j];sum[j]=sum[j+1];sum[j+1]=t;num++;}}}printf("排序后的顺序为:\n");for(i=0;i<n;i++){printf(sum[i]+" ");if(sum[i]==1){printf("白 ");}else{printf("黑 ");}}printf("\n一共换位了%d次",num);printf("\n");return 0;
}交替放置的碟子
1、实验结果

2 算法复杂度分析
时间复杂度:O(n(n+1)/2)
五、实验小结(包括问题和解决方法、心得体会等)
通过这次实验,我对算法设计有了更深的认识。在以前的学习中,我认为代码部分是最困难的,而现在我的观念有了转变。很多的问题是源于生活的,大多算法的规则不会像数学公式一样刻板规矩,我们在学习算法的过程中最先要做的是,学会分析实际问题,形成算法思想。在厘清题意的基础上编写实验代码,编译运行后进行相应的优化改进,在解决问题的过程中逐渐提高自己的逻辑思维能力和编程能力。









)
)




![[Spring Cloud] gateway全局异常捕捉统一返回值](http://pic.xiahunao.cn/[Spring Cloud] gateway全局异常捕捉统一返回值)


)
