算法学习18:动态规划
文章目录
- 算法学习18:动态规划
- 前言
- 一、线性DP
- 1.数字三角形:f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
- 2.1最长上升子序列:f[i] = max(f[i], f[j] + 1);
- 2.2 打印出最长子序列
- 3.最长公共子序列:
- 二、区间dp:
- 1.石子合并:
- 总结
前言

提示:以下是本篇文章正文内容:
一、线性DP
1.数字三角形:f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
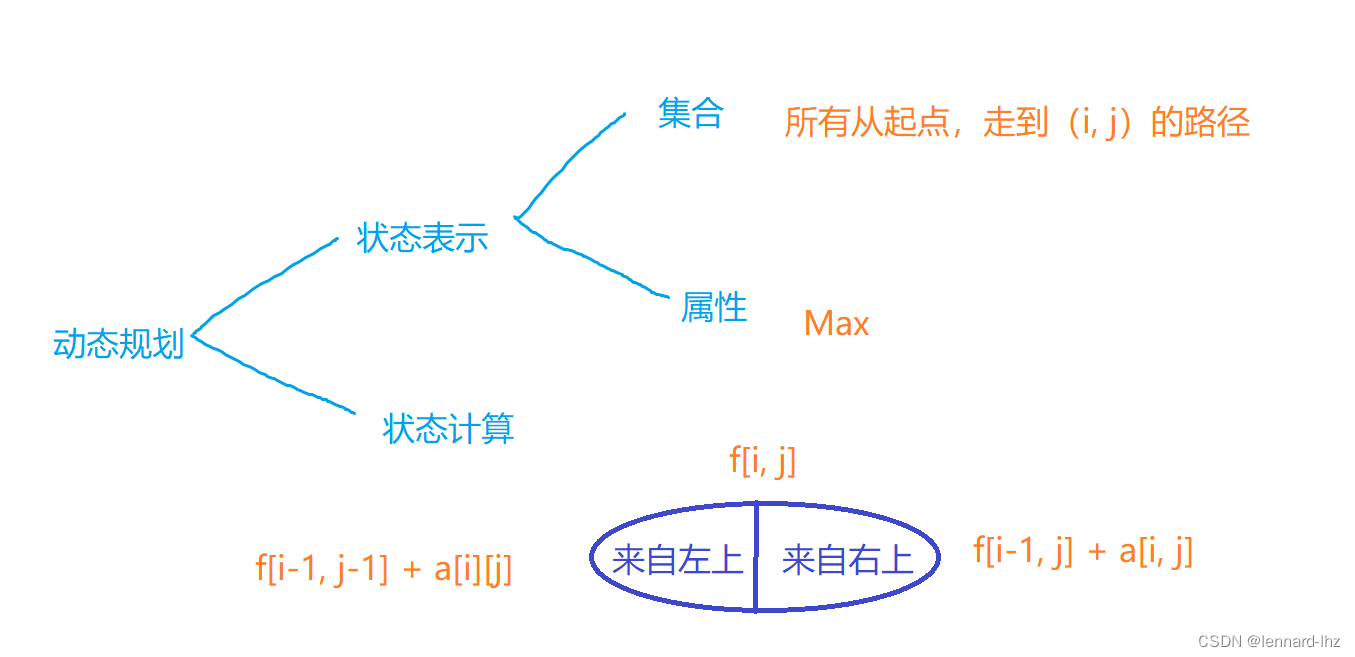

// 给定一个数字三角形,从顶部出发,在每一个结点可以选择移动至左下方或者是右下方的结点,
// 直到移动到底层,要求找到一条路径,使得路径上的数字的和最大。
// 输入:第一行包含一个整数n,表示数字三角形的层数
// 接下来的n行,每行包含若干整数,其中第i行表示数字三角形第i层包含的整数。#include <iostream>
#include <algorithm>using namespace std;const int N = 510, INF = 1e9;// (相对的)正无穷 int n;
int a[N][N];// 存出数字三角形
int f[N][N];// 状态 int main()
{scanf("%d", &n);for(int i = 1; i <= n; i ++)for(int j = 1; j <= i; j ++)scanf("%d", &a[i][j]);// 初始化// 注意1:对于左右边界,都要多处理一次。(i+1) for(int i = 0; i <= n; i ++)for(int j = 0; j <= i + 1; j ++)f[i][j] = -INF;// 负无穷 f[1][1] = a[1][1];for(int i = 2; i <= n; i ++)for(int j = 1; j <= i; j ++)f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);int res = -INF;// 遍历最后一层,找到答案 for(int i = 1; i <= n; i ++) res = max(res, f[n][i]);printf("%d\n", res);return 0;}
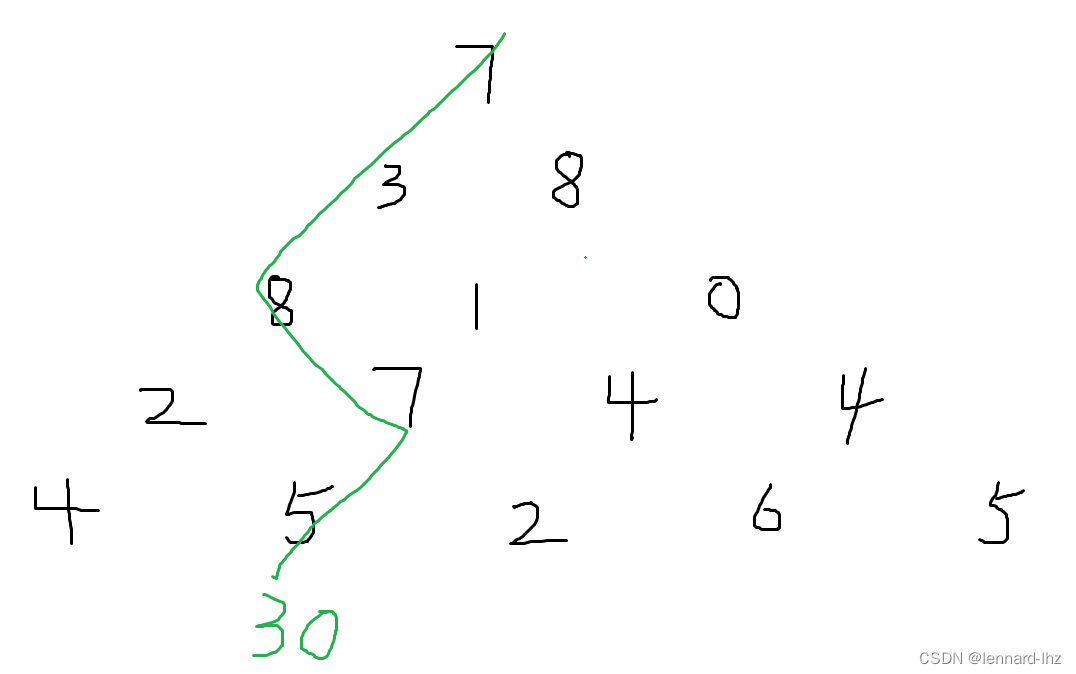

2.1最长上升子序列:f[i] = max(f[i], f[j] + 1);
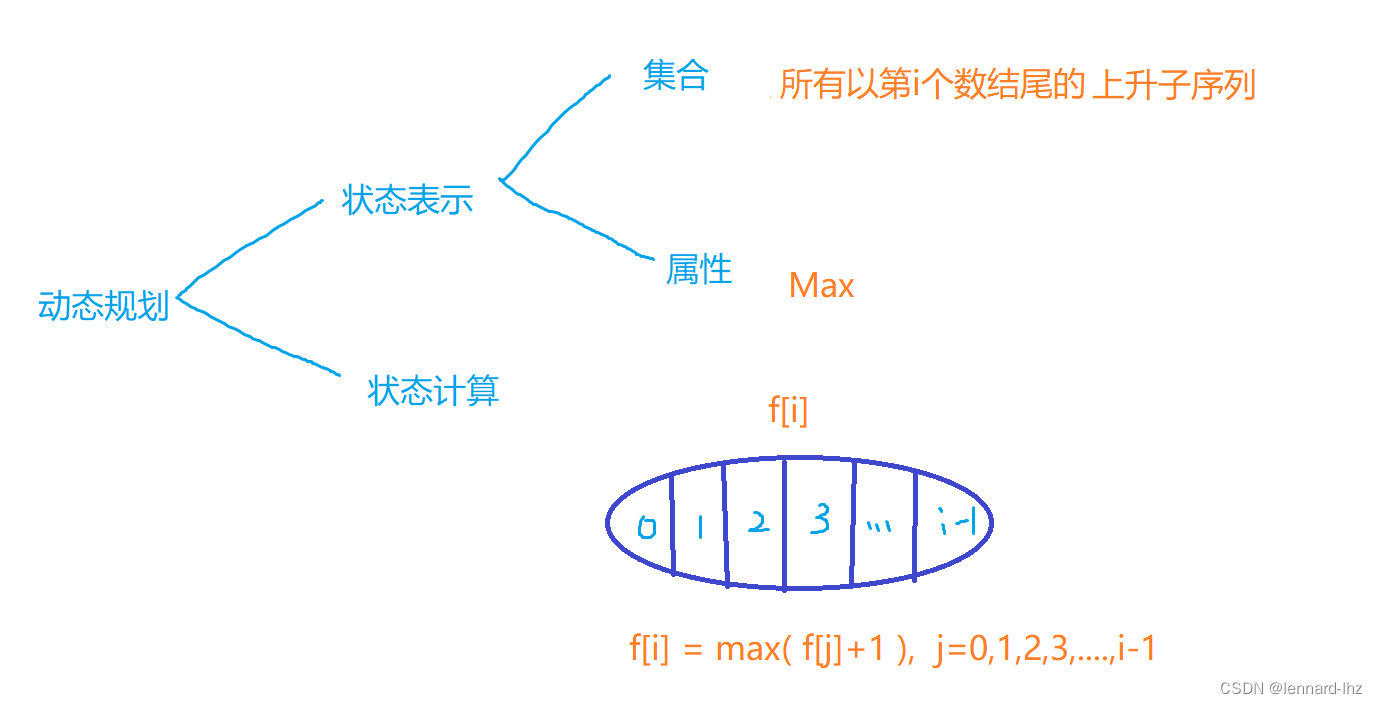
2.2 打印出最长子序列
// 给定一个长度为n的数列,求数值“严格递增”的子序列的长度最长时多少?#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n;
int a[N], f[N], g[N];// 数列 状态 存储i是由那个状态转移过来的。 int main()
{scanf("%d", &n);for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);for(int i = 1; i <= n; i ++){f[i] = 1;// 只有a[i]一个数g[i] = 0; for(int j = 1; j < i; j ++)// 保证递增:a[j] 是 a[i] 的前一个数 if(a[j] < a[i])if(f[i] < f[j] + 1){// 更新 f[i] = f[j] + 1;// 记录一下f[i] 是从哪一个状态转移过来的。 g[i] = j;} }// 找到答案的下标 int k = 1;for(int i = 1; i <= n; i ++)if(f[k] < f[i]) k = i;printf("%d\n", f[k]);// 长度 for(int i = 0, len = f[k]; i < len; i ++){printf("%d ", a[k]);// 根据g数组可以知道f[k]是从那个状态转移的 k = g[k];}return 0;
}
// 给定一个长度为n的数列,求数值“严格递增”的子序列的长度最长时多少?#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n;
int a[N], f[N];// 数列 状态 int main()
{scanf("%d", &n);for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);for(int i = 1; i <= n; i ++){f[i] = 1;// 只有a[i]一个数for(int j = 1; j < i; j ++)// 保证递增:a[j] 是 a[i] 的前一个数 if(a[j] < a[i])f[i] = max(f[i], f[j] + 1); }int res = 0;// 便利所有f[i] for(int i = 1; i <= n; i ++) res = max(res, f[i]);printf("%d", res);return 0;
}
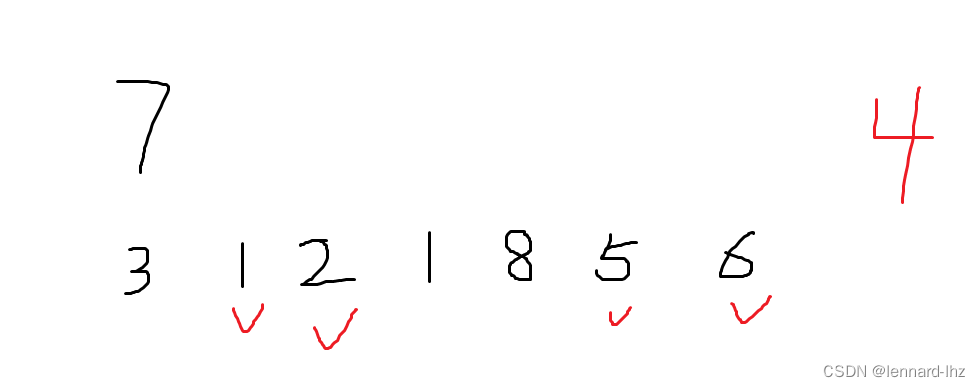
3.最长公共子序列:
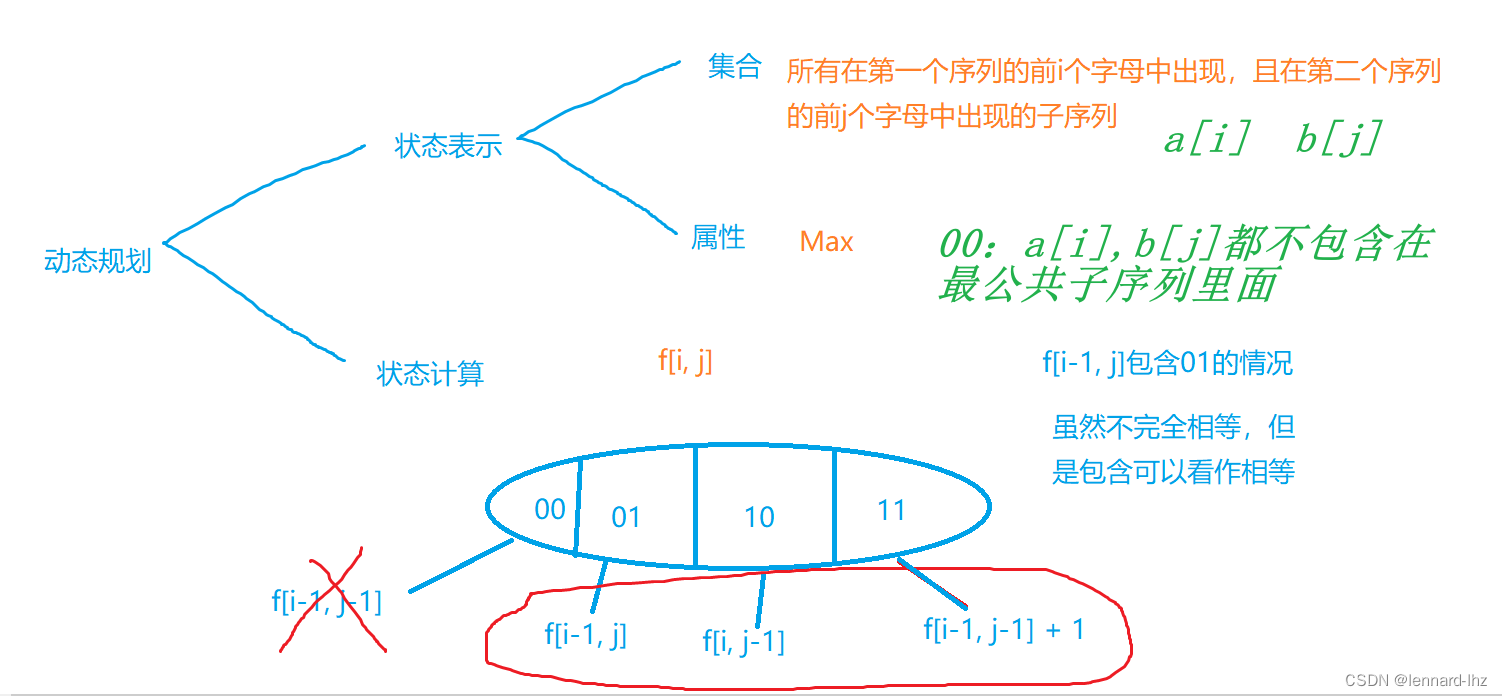

// 给定两个长度分别为n和m的字符串A和B,
// 求即是A的子序列又是B的子序列的字符串的长度最长是多少?
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n, m;
char a[N], b[N];// 2个字符串
int f[N][N]; int main()
{scanf("%d%d", &n, &m);scanf("%s%s", a + 1, b + 1);// 注意1:从a[1]开始输入字符串// 从1开始遍历 for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++){f[i][j] = max(f[i - 1][j], f[i][j - 1]);if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);} printf("%d\n", f[n][m]);return 0;
}
二、区间dp:
1.石子合并:
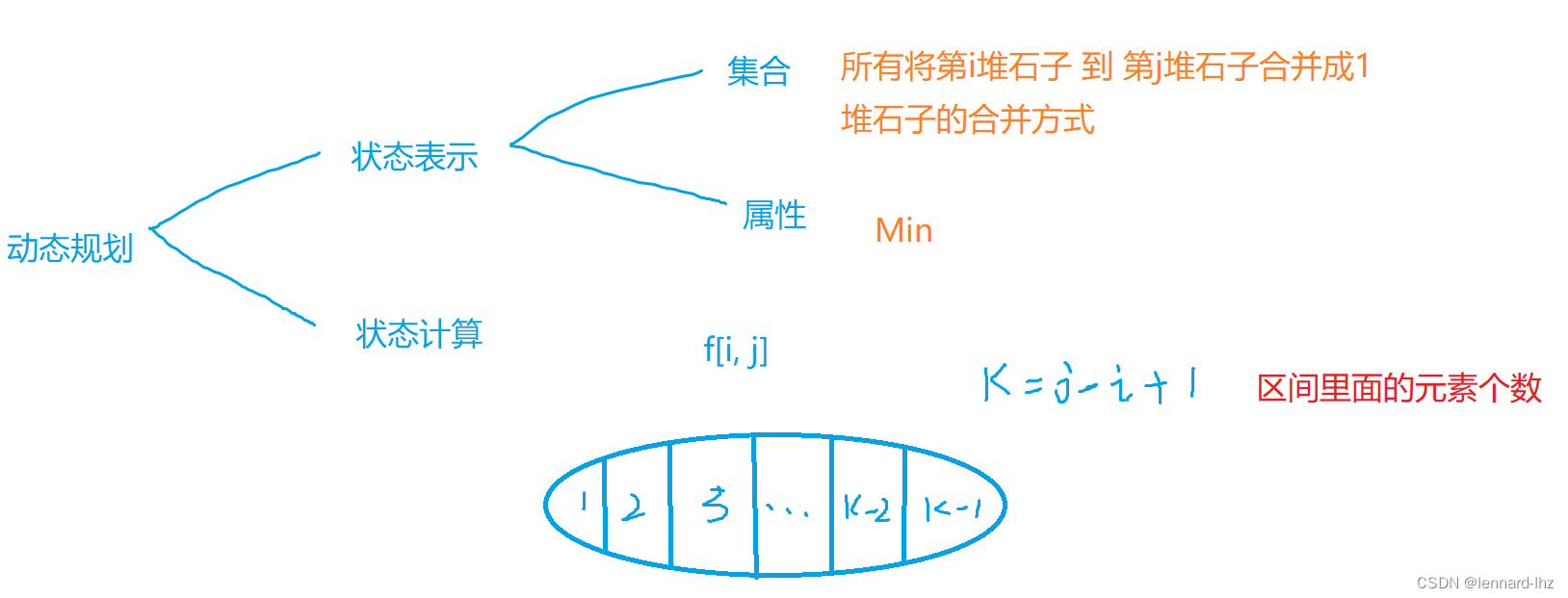


// 设有n堆石子排成一排,其编号为1,2,3,......,n
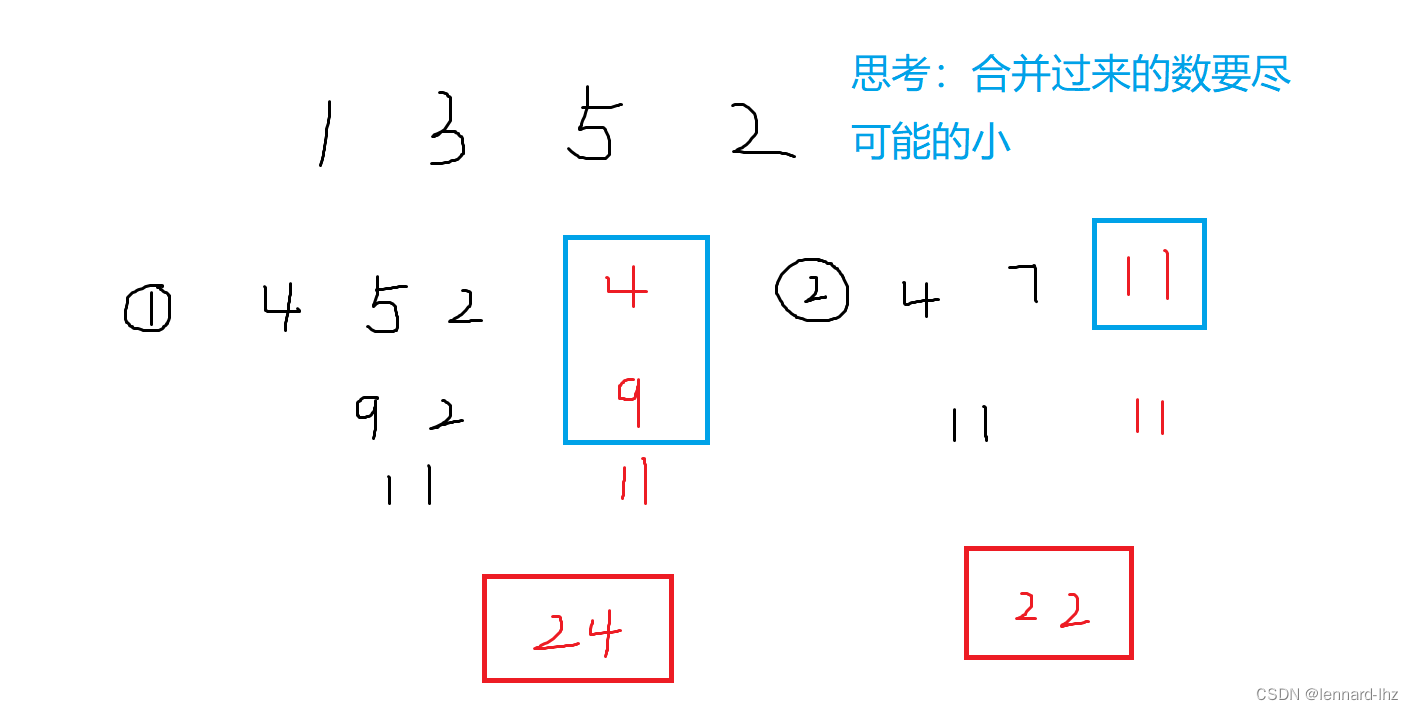
// 用一个整数描述每堆石子的质量,现在要将这n堆石子合并为一堆。// 例子1:有1 3 5 2四堆石子,我们可以先合并1、2堆,代价为4,得到4 5 2,又合并1、2堆,
// 代价为9,得到9 2,在合并得到11,总代价:4+9+11=24
// 例子2:先合并1和2、3和4堆,代价为4+7,得到4 7,再合并,代价为11,总代价:4+7+11=22
#include <iostream>
#include <algorithm>using namespace std;const int N = 310;int n;
int s[N];// 原始数据
int f[N][N];int main()
{scanf("%d", &n);for(int i = 1; i <= n; i ++) scanf("%d", &s[i]);// 前缀和数组: for(int i = 1; i <= n; i ++) s[i] += s[i - 1];// 按长度从小到大枚举所有状态:从2开始 // 区间长度为1:不需要代价 for(int len = 2; len <= n; len ++)// 枚举起点: for(int i = 1; i + len - 1 <= n; i ++){// 左右端点: int l = i, r = i + len - 1;f[l][r] = 1e8;// 要初始化为一个比较大的数!!! // 枚举分界点: for(int k = 1; k < r; k ++)f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);}printf("%d\n", f[1][n]);return 0;}
总结
提示:这里对文章进行总结:
💕💕💕



)







:对象To数组——规则属性重组)







