一、系统稳定性

 

在控制理论中，系统稳定性是一个非常关键的概念，它主要涉及系统对外界扰动或内部变动的响应行为。以下是与系统稳定性相关的一些核心名词及其解释：

基本概念

稳定性（Stability） 系统稳定性是指当系统受到外部扰动后，在扰动消失后系统能够回到或保持在某个确定的平衡状态，或者在有限时间内其输出趋于一个可接受范围内的过程。简单来说，如果系统在扰动下不会发散或无限增长，而是保持有限的变化，我们就称该系统是稳定的。

平衡状态（Equilibrium State） 在控制系统中，平衡状态通常是指没有外加输入信号时，系统的输出保持恒定不变的状态。

线性系统稳定性 对于线性系统，可通过分析系统的特征根（如传递函数的极点位置）来判断系统的稳定性。如果所有闭环极点都在s平面的左半部分（实部小于零），则系统是BIBO（bounded input, bounded output）稳定的，这意味着当输入是有界的时，输出也会是有界的。

绝对稳定性（Absolute Stability） 对于连续时间线性系统，绝对稳定是指系统对于任何有界输入都产生有界输出的性质。

相对稳定性（Relative Stability） 相对稳定性关注的是系统动态响应的品质，不仅要求系统稳定，还关注超调量、调节时间和稳定性边界等问题。例如，在线性系统中讨论幅值裕度和相位裕度就属于相对稳定性的范畴。

Lyapunov稳定性 基于Lyapunov理论的稳定性包括全局稳定性、局部稳定性、渐进稳定性等，它不仅仅依赖于系统的微分方程结构，而是通过构造Lyapunov函数来分析系统在不同条件下的稳定性。

瞬态响应 瞬态响应是指系统在受到阶跃输入或脉冲输入等扰动后的短期行为，考察系统能否迅速并准确地达到新的稳态。

稳态误差 稳态误差是指系统在响应结束后，输出量与期望值之间的差异，它是衡量控制系统精准度的一个重要指标。

李雅普诺夫第二法 李雅普诺夫第二法用于判断系统的渐进稳定性，即当系统从任意初始状态出发，其状态是否随时间趋于某个吸引域或平衡点。

相关术语

• 稳定区域（Stable Region）: 控制系统参数空间中的区域，其中的每一个点对应的系统都是稳定的。
• 临界稳定性（Marginal Stability）: 系统刚好满足稳定性条件但稳定程度较差，一般对应于系统具有位于复平面虚轴上的极点。
• 不稳定（Unstable）: 当系统在扰动下输出持续增长且无法收敛到某一确定状态时，系统被认为是不稳定的。

通过这些概念，工程师可以设计和分析控制系统，确保系统在各种工作条件下都能保持预期的行为和性能。

 

二、稳定性证明方法

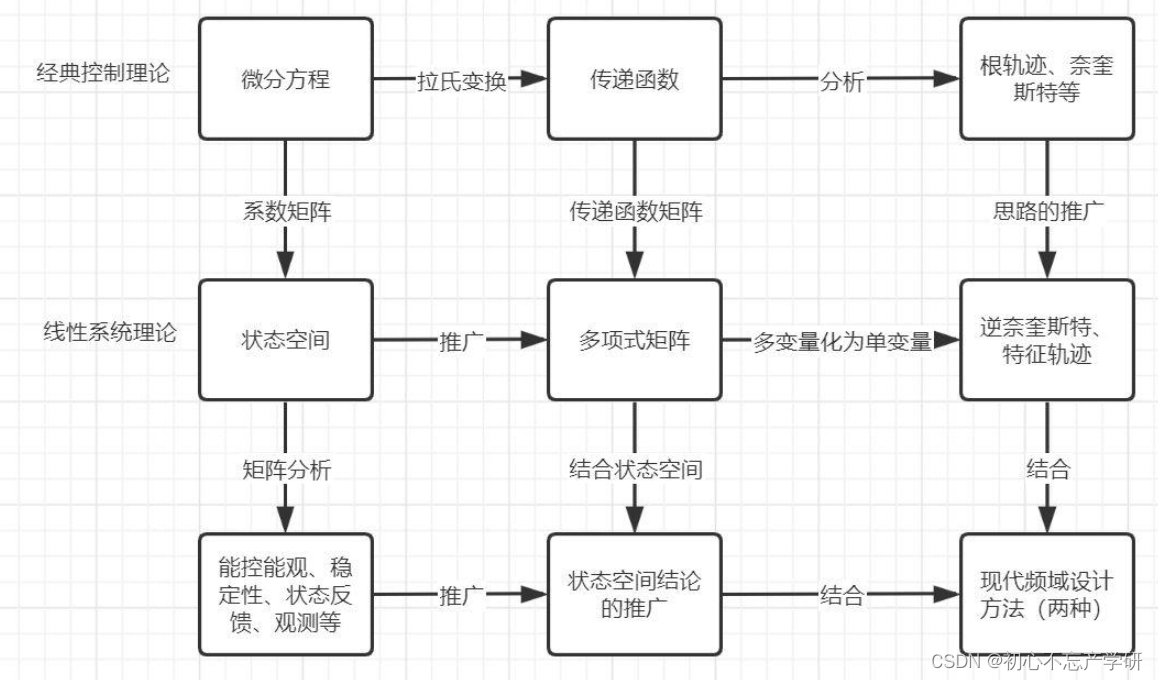
控制理论的稳定性证明方法的发展历程涵盖了从经典控制理论到现代控制理论的多个里程碑式的进步，以下是详细的叙述：

经典控制理论阶段：
1. 劳斯-赫尔维茨稳定判据（Routh-Hurwitz Stability Criterion）
劳斯稳定判据最早由爱德华·劳斯在1877年提出，赫尔维茨随后进行了进一步发展和完善。这一判据针对的是线性定常系统，它通过构造劳斯表（Routh array）并检查其元素符号来判断线性系统的特征方程的所有根是否都在复平面的左半部（负实轴左侧），从而确定系统是否稳定。

2. 根轨迹法
根轨迹分析方法起源于20世纪40年代，是一种图形化的方法，通过绘制系统的根轨迹来研究闭环极点的变化趋势，进而判断系统在参数变化范围内的稳定性。

3. 奈奎斯特稳定判据（Nyquist Stability Criterion）
哈利·奈奎斯特在1932年提出的该判据是基于频率域分析的稳定性准则，通过对闭环传递函数的奈奎斯特图进行分析，通过包围(-1, j0)点的次数来判断闭环系统的稳定性。

现代控制理论阶段：
4. 李雅普诺夫稳定性理论
19世纪末期，俄国数学家亚历山大·米哈伊洛维奇·李雅普诺夫创立了一种全新的稳定性分析方法。他首先提出了李雅普诺夫第一方法，通过构造一个能度量系统动态偏离平衡状态程度的能量函数（或称李雅普诺夫函数）来证明系统的稳定性。而李雅普诺夫第二方法则引入了泛函分析的思想，通过寻找一个称为Lyapunov函数的实值函数，其时间导数在系统的整个状态空间内非正或者负定，从而证明系统的稳定性。

5. 状态空间方法与特征值分析
在20世纪中叶，随着电子计算机的出现和发展，状态空间方法逐渐成为主流。通过建立系统的状态空间模型，并分析其对应的特征值，可以直接得出系统稳定性结论。对于线性定常系统而言，所有特征值具有负实部意味着系统稳定。

6. 李雅普诺夫方法在现代控制理论中的扩展
现代控制理论中，李雅普诺夫方法得到了广泛应用，尤其是在线性矩阵不等式（LMI）、滑模控制、变结构控制等领域，这些方法允许对系统设计更复杂的稳定化控制器，并能处理非线性系统的局部稳定性问题。

非线性系统稳定性理论的进展：
7. 非线性系统的全局与局部稳定性
针对非线性系统的稳定性，出现了多种专门的理论和方法，比如相图分析、李雅普诺夫函数的构造、分叉理论、中心流形理论等，它们用于分析非线性系统的全局稳定性、局部稳定性、混沌现象以及稳定性边界等。

鲁棒稳定性和最优控制理论：
8. 鲁棒稳定性理论
随着控制理论对实际工程系统中不确定性因素的关注增加，鲁棒稳定性理论得到了深入发展。这包括H∞控制理论、μ分析、滑模鲁棒控制等，这些理论旨在设计控制器保证系统在存在模型不确定性或外部扰动时仍然保持稳定。

总之，控制理论的稳定性证明方法历经一个多世纪的发展，不断吸收新的数学工具和思想，从简单的多项式系数分析扩展到了对非线性、时变、不确定系统的全面理解和稳健控制设计，极大地推进了自动化控制领域的实践与发展。

此图片来源于网络 

 

三、稳定性的意义

稳定性证明在控制理论中之所以重要，是因为它直接关乎着控制系统的性能、安全性和有效性。一个不稳定的控制系统会对其所控制的过程产生不可预测的结果，可能导致系统输出无限制的增长、振荡过大或出现物理不可接受的行为，这在许多工程应用中是灾难性的，比如航天器姿态控制、化工过程控制、电力系统稳定、机械臂操作等领域。稳定性分析能确保系统在正常运行和遇到扰动时都能够保持可控，避免潜在的风险和损失。

系统稳定性和产品的可靠性之间存在着紧密联系：

1. 可靠性保证的基础：稳定性是控制系统可靠性的前提条件之一。只有当系统在各种工作条件下都保持稳定，才能保证系统在长期运行过程中不会因为内部或外部扰动而发生失效，从而提高产品的使用寿命和安全性。

2. 性能约束：稳定的系统意味着其输出响应会在一定程度上收敛或维持在一个可接受的范围内，这对于评价和提高产品的性能至关重要。例如，在实时控制中，快速且稳定的响应有助于提升工作效率和产品质量。

3. 鲁棒性设计：在设计过程中，通过对系统稳定性的深入研究和严格证明，工程师能够设计出具有更强抗干扰能力和适应性变化能力的控制系统，进而增强产品的整体可靠性。

4. 故障预防与恢复：稳定的控制系统在面对意外故障时，能够更快地恢复到正常工作状态，这是系统可靠性的重要体现。

总结来说，控制系统的稳定性不仅是系统本身功能实现的基础，更是保障产品在复杂环境下长期有效、安全运行的关键要素，直接影响到产品的可靠性水平。