简介
受限于MCU自身的ADC外设缺陷,精度和稳定性通常较差,很多场景下需要用滤波算法进行补偿。滤波的主要目的是减少噪声与干扰对数据的影响,让数据更加接近真实值。
一阶低通滤波
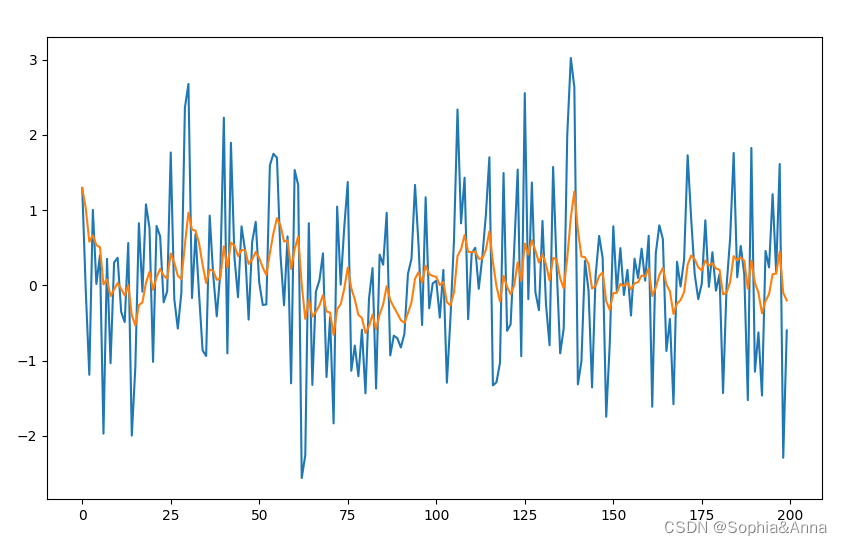
一阶低通滤波是一种信号处理技术,用于去除信号中高频部分,保留低频部分。在滤波过程中,一阶低通滤波器会使得高于某个截止频率的信号被衰减,而低于截止频率的信号则会被保留。这有助于减少噪音或者不需要的信号成分,从而提高信号的质量。
典型案例:蓝牙耳机、音响
Python实现
import numpy as np
import matplotlib.pyplot as plt
# 生成示例数据
sensor_data = np.random.randn(200) # 正态分布随机数据
# 定义低通滤波函数
def low_pass_filter(data,cutoff_freq):filtered_data = np.copy(data)for i in range(1,len(data)):filtered_data[i] = (1-cutoff_freq)*filtered_data[i-1]+cutoff_freq*data[i]return filtered_data
# 设置截止频率
cutoff_freq = 0.2
# 应用低通滤波
filter_sensor_data = low_pass_filter(sensor_data,cutoff_freq)
# 绘制原始数据和滤波后数据
plt.figure(figsize=(10,6))
plt.plot(sensor_data)
plt.plot(filter_sensor_data)
plt.show()C实现
均值滤波

说明:连续取N个采样值进行算术平均运算达到降噪目的;
N值较大时:信号平滑度较高,但灵敏度较低
N值较小时:信号平滑度较低,但灵敏度较高
优点:试用于对一般具有随机干扰的信号进行滤波。这种信号的特点是有一个平均值,信号在某一数值范围附近上下波动。
缺点:测量速度较慢或要求数据计算较快的实时控制不适用。
典型案例:电子秤...
Python实现
import numpy as np
import matplotlib.pyplot as plt
# 生成模拟示例数据
sensor_data = np.random.randn(200) # 正态分布随机数据
m = 0 # 起始角标
n = 11 # 在多少个数中取中间值,必须为奇数
def average_filter(data):global m,ndata = sensor_data[m:m+n]m +=nvalue = np.average(data)return valuefilter_sensor_data = np.zeros_like(sensor_data)for i in range(0, len(sensor_data),n):filter_sensor_data[i] = average_filter(sensor_data)# 绘制原始数据和滤波后数据
plt.figure(figsize=(10,6))
plt.plot(sensor_data,c="green")
plt.plot(filter_sensor_data,c="red")
plt.show()C实现
滑动平均滤波
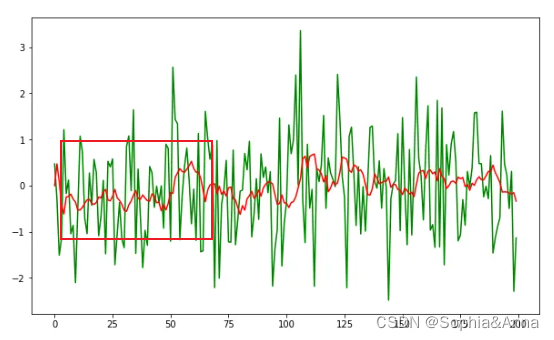
说明:把连续取N个采样值看成一个队列,队列的长度固定为N。每次采样到一个新数据放入队尾,并扔掉原来队首的一次数据(先进先出原则)。把队列中的N个数据进行算术平均运算,就可获得新的滤波结果。
N值的选取:流量,N=12;压力:N=4;液面,N=4~12;温度,N=1~4
优点:对周期性干扰有良好的抑制作用,平滑度高;试用于高频振荡的系统
缺点:灵敏度低;对偶然出现的脉冲性干扰的抑制作用较差,不适于脉冲干扰较严重的场合比较浪费RAM(改进方法,减去的不是队首的值,而是上一次得到的平均值)
典型应用:汽车上剩余可行驶里程预估
Python实现
import numpy as np
import matplotlib.pyplot as pltsensor_data = np.random.randn(200)
n = 11
filter_sensor_data = np.zeros_like(sensor_data)
for i in range(1,len(sensor_data)):if i<n:temp_data = sensor_data[0:i]value = np.average(temp_data)filter_sensor_data[i] = valueelse:temp_data = sensor_data[i-n:i]value = np.average(temp_data)filter_sensor_data[i] = value
plt.figure(figsize=(10,6))
plt.plot(sensor_data,c="green")
plt.plot(filter_sensor_data,c="red")
plt.show()C实现
中值滤波

说明:连续采样N次(N取奇数)把N次采样值按大小排列取中间值为本次有效值
优点:能有效克服因偶然因素引起的波动干扰;对温度、液位等变化缓慢的被测参数有良好的滤波效果
缺点:对流量,速度等快速变化的参数不宜。
典型应用:电子秤....
Python实现
import numpy as np
import matplotlib.pyplot as plt
# 生成模拟数据
sensor_data = np.random.randn(200) # 正态分布随机数据# 起始角标
m = 0
n = 11 # 在多少个数中取中间值,必须为奇数# 定义中值滤波算法
def middle_filter(data):global m,ndata = sensor_data[m:m+n]m += ndata2 = sorted(data)# 取中间值middle_index = int(len(data2)/2)value = data2[middle_index]return value
filter_sensor_data = np.ones_like(sensor_data)
# 绘制原始数据和滤波后数据
for i in range(0,len(sensor_data),n):filter_sensor_data[i] = middle_filter(sensor_data)
plt.figure(figsize=(10,6))
plt.plot(sensor_data,c="blue")
plt.plot(filter_sensor_data,c="red")
plt.show()
C实现
卡尔曼滤波
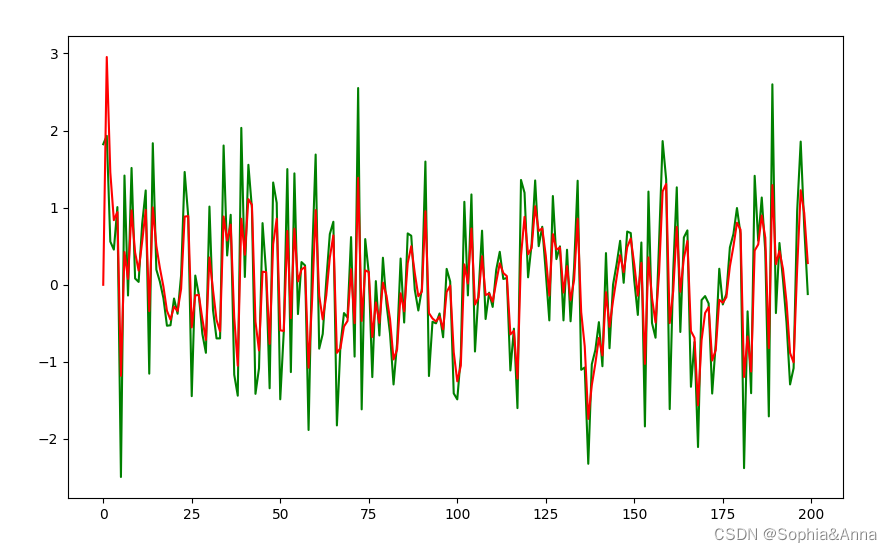
说明:根据当前的仪器"测量值" 和上一刻的 “预测量” 和 “误差”,计算得到当前的最优量,再预测下一刻的量。里面比较突出的是观点是:把误差纳入计算,而且分为预测误差和测量误差两种,通称为噪声。还有一个非常大的特点是:误差独立存在,始终不受测量数据的影响。
优点:巧妙的融合了观测数据与估计数据,对误差进行闭环管理,将误差限定在一定范围。适用性范围很广,时效性和效果都很优秀。
缺点:需要调参,参数的大小对滤波的效果影响较大。
典型应用:卫星轨迹预测、火箭发射、无人机与机器人运动控制....
Python实现
class KalmanFilter:def __init__(self,q=0.001,r=0.001) -> None:self.q = q # 过程噪声协方差self.r = r # 测量噪声协方差self.p = 5 # 估计误差协方差self.k_gain = 0 #卡尔曼增益self.prev_data = 0 # 先前数据值def updata(self,measurement):# 预测self.p +=self.q# 计算卡尔曼增益self.k_gain = self.p/(self.p+self.r)# 更新估计值estimation = self.prev_data + self.k_gain*(measurement-self.prev_data)# 更新估计误差协方差self.p = (1-self.k_gain)* self.p# 更新先前数据值self.prev_data = estimationreturn estimation# 测试
kf = KalmanFilter()
input_data = 5
filter_data = kf.updata(input_data)
print(f"滤波后:filter_data")import numpy as np
import matplotlib.pyplot as plt
sensor_data = np.random.randn(200)
n = 11
filter_sensor_data = np.zeros_like(sensor_data)
for i in range(1,len(sensor_data)):src_data = sensor_data[i]filter_sensor_data[i] = kf.updata(src_data)plt.figure(figsize=(10,6))
plt.plot(sensor_data,c="green")
plt.plot(filter_sensor_data,c="red")
plt.show()


)









)





)