一、自然界中的材质
首先了解下自然界中的材质

如上这幅图,不同的物体、场景、组合,会让我们看到不同的效果。
我们通常认为物体由其表面定义,表面是物体和其他物体或周围介质之间的边界面。但是物体内部的材质也会影响光照效果。我们目前只考虑两种不同介质间的边界面,并假定光穿过边界面后有不同的传播方式。
但是归根到底就一个核心:光线如何传播的,又是如何跟物体作用的。
研究自然界中的材质,就是在研究光线如何传播
光与材质的交互作用非常简单。作为基本的类似,每个击中物体表面的光子有三种情况:
- 被吸收并转换成热能
- 穿过表面进入物体内部
- 被表面反射出去
每一种情形出现的概率和发生作用后光子的传播方向由物体的材质以及撞击点附近表面微表面的朝向所决定。
二、 计算机图形学中的材质
如下3D的由四边形组成的模型,右边是渲染后的图,表现为陶瓷杯,为啥就能看出是陶瓷? 因为在渲染方程中通过对BRDF函数的定义,使杯子表现了一定程度的镜面反射+漫反射,给人一种陶瓷感。

一般情况下,我们至少需要区分以下五种在审美和感知上有意义的现象:
- 清晰的镜面反射,如玻璃上的反光
- 具有光泽的高光和反射,例如涂蜡苹果上的高光
- 表面下的浅层散射,他导致独立于观察方向的朗伯漫反射,例如平坦墙上涂料的观察效果
- 表面下的深层反射,这是由于光在表面下的漫散射,是皮肤和大理石等外观较柔和的原因
- 透射,当光通过几乎透明的材质(如水和雾)时,进入介质后发生折射。在光的路径上可能有少量的漫反射
因为这些现象都源于散射(或者由于被吸收而无散射),所以常使用散射函数进行描述,有几种散射函数,其中包括:
- 用于描述表面散射的双向散射分布函数–BSDF
- 仅考虑不透明表面反射的双向反射分布函数–BRDF
- 用于纯透射表面的双向透射分布函数–BTDF
- 用于描述表面反射和表面下浅层散射效果的双向散射反射分布函数–BSSDF
2.1 漫反射材质的BRDF

漫反射的BRDF推导过程:
假设入射光是均匀分布在半球上的并且处处相等,漫反射光也一样
由能量守恒可以知道入射的照度Irradiance == 出射的Irradiance,并且入/出射都是均匀分布,那么他们各自某个立体角的radiance也相等,即 Lo = Li 建立渲染方程如下:

对cosθ在半球上的定积分结果为π(过程省略),最终可得到完全不吸收能量的漫反射BRDF项fr为: 1 / π
还可以定义 ρ 反射率albedo,可以是单通道(0~1)、三通道(RGB),从而可以引入不同颜色的漫反射BRDF
2.2 抛光/毛面金属材质的BRDF
这种材质散射规律是在镜面反射方向附近,一小块区域进行均匀的散射,用代码实现的话也很简单,算出镜面反射方向(x,y,z),就以(x,y,z)为球心(圆心也行),随机在球内生成一个点,以反射点到这个点作为真的反射方向。这样的话,高一点的SPP下,就能够均匀的覆盖镜面反射方向附近的一块小区域了

2.3 完全镜面反射+折射材质的BRDF
折射方向稍微难算一些,镜面反射方向简单。
这种材质与光的作用方式可分为射入和射出(默认折射率η比空气大)
- 从空气射入材质内部,则一定是镜面反射+折射同时发生
- 如果从材质内部射入空气,则分两种情况: 镜面反射+折射 不满足折射条件,仅镜面反射。

2.3.1 镜面反射方向(立体角)计算
已知入射方向向量为,则反射方向向量 = V + 2B
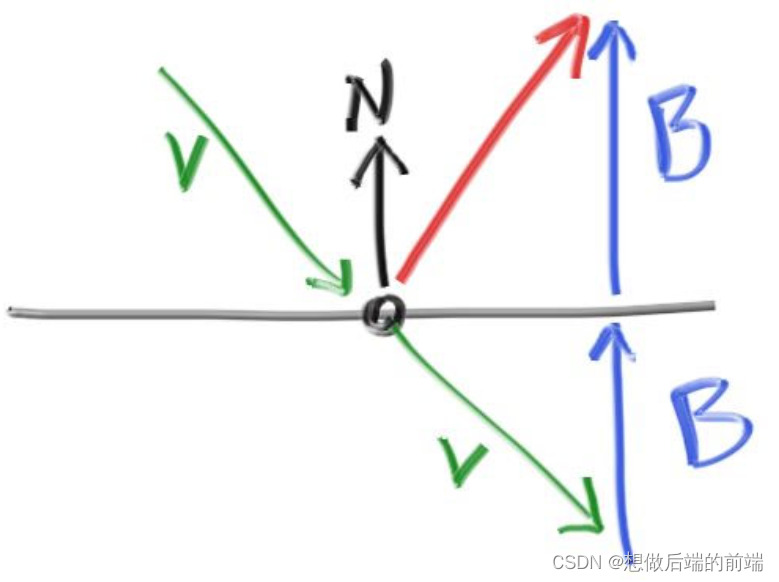
这里其实可以看出来,计算镜面反射方向其实还是有那么点麻烦的吧,所以之前进行Blinn-Phong模型着色计算时,高光项判断出射方向是否足够接近镜面反射时,没有用镜面反射方向与出射方向做比较,而是用半程向量half vector跟法线n来比,半程向量计算非常简单:入射+出射然后单位化就行了。
如果天顶角+方位角的形式来描述三维空间的一个方向,则出射方向计算很简单
方位角φ,他们必然在一个面上,并且相差180°,满足下面这个方程
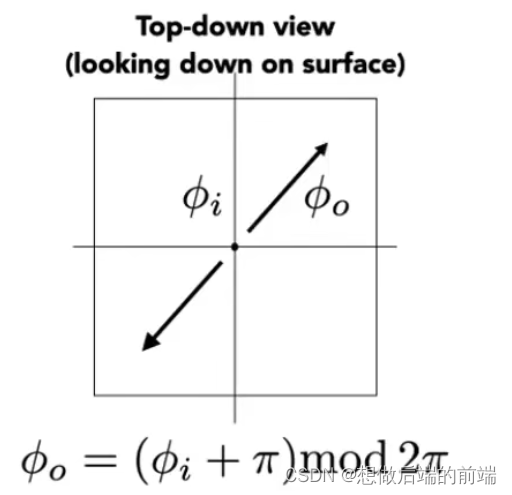
天顶角θ:镜面反射的入射和出射的θ是相等的

2.3.2 折射方向计算
光从一种介质进入到另一种介质就会发生折射。
第三幅图水底的这种现象称为caustics,这是由于水面凹凸不平,水底某些点会聚集较多的光线,有点聚焦的意思。

折射方向计算:
斯内尔定律(Snell’s Law): 给出了描述光从一种介质传播到另一种介质时是如何折射的方程:ηisinθi = ηtsinθt
必须知道两种材质的折射率η1,η2,和入射角度θi,然后能得到θt;再根据入射和出射的方位角关系公式,能算出φt。θt和φt组成ωt
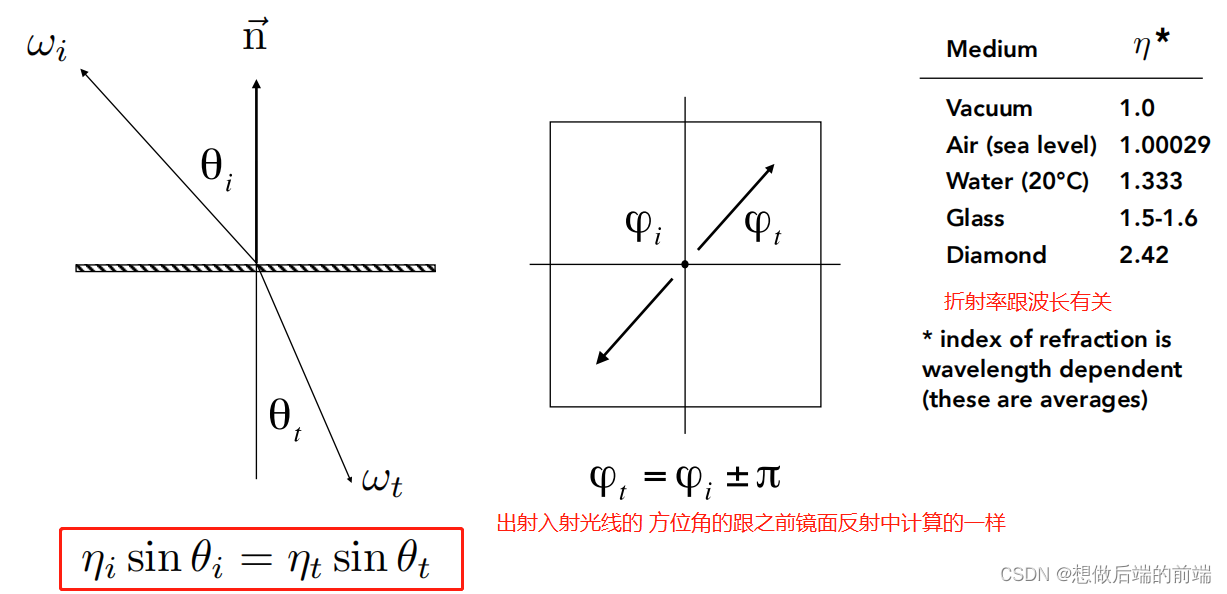
折射发生的条件:
- 光疏介质->光密介质:必然折射
- 光密介质->光疏介质:根据入射角度大小,过大可能就没有折射而是全反射
所以会有一个全反射和折射的临界角
证明:
由折射方程:ηisinθi = ηtsinθt,sin2θ + cos2θ = 1可知
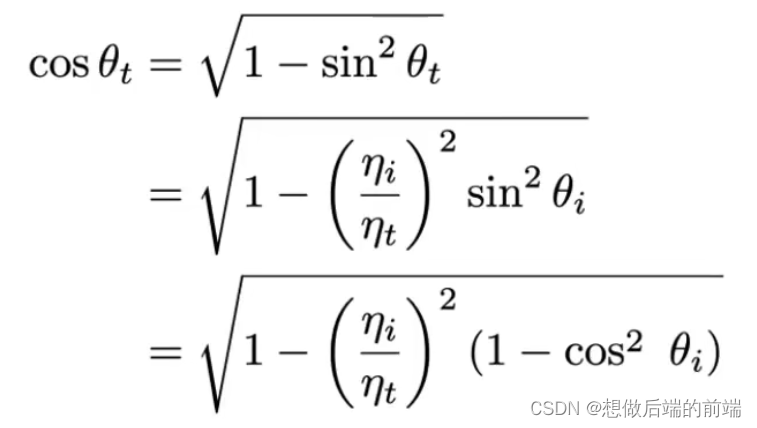
看根号内的式子(首先1-cos2θi < 1 恒成立)
当ηi/ηt < 1,根号下式子 > 0,等式有意义,必然发生折射 。
当ηi/ηt > 1,具体看1-cos2θi 的大小,如果入射角θi比较大,根号下式子可能会 < 0。
例子:水介质和光介质

两个角度看这张图:
(1)光从空气射入水中,可以明显看到,空气中不管角度多大都会发生折射
(2)记住图形学中考虑问题都是摄像机发射光线,光线从水中射入空气,只能看到大概97.2°的一个锥形区域的光,角度再大一点就发生全反射了。所以超过这个锥形区域,其他地方的光都射向水底了,比较黑。
三、菲涅尔项(Fresnel Term)
反射率取决于入射角度,入射光与法线的夹角越大,反射的能量越多
从书上反射出的光,射到桌面然后反弹到人眼中,如果入射光跟法线夹角比较小(左1),则几乎看不到桌面的倒影,即反射能量比较少;当入射光跟法线夹角特别大,几乎接近90°的时候,桌面会形成比较明显的书的倒影,也就是能量衰减得比较少
入射角度与反射率关系曲线图
- 绝缘体(非金属) : 可以看到如果一根光线跟法线几乎成90°的话,反射率几乎为1,没有能量损失虚线可以不看,这部分是偏振光的性质,实线是两个方向偏振光取平均的结果,看红实线即可

- 导体(金属物品) : 不管什么角度反射率都蛮高的

菲涅尔项的计算:
精确计算菲涅尔项(没有必要)
求s、p偏振光的菲涅尔项,然后取两者的平均作为最终结果
计算挺复杂,明白这玩意儿跟出/入射角度、介质反射率η有关就行了
近似计算:Schlick’s approximation(性价比更高)
- R(θ)函数,自变量θ为入射光线与法线夹角,定义域在[0°,90°],返回值为反射率,值域[0,1]
- Schlick提出这个计算方式,其实就是重新拟合了一条曲线,近似的表现上面介绍的“入射角度与反射率关系曲线图”。R0就是入射光与法线夹角为0时的反射率。
- 我们如果代入θ = 0,θ = 90,进去算很容易看出R(0) = R0,R(90) = 1,还是比较正确的。这个函数同时适用于导体和绝缘体。
- n1,n2是两种介质的折射率

在这里提到菲涅尔项的目的:引出微表面材质/模型
四、 微表面材质(Microfacet Material)
研究微表面材质的动机是什么?—— 因为现实生活中,确实有这种现象存在
如下,卫星拍摄的一幅图,这片高光的效果看起来像平面,但我们知道它是凹凸不平的
只要当视角离得足够远,我们看不到表面的细节,只能看到光对该表面整体的作用结果

4.1 微表面模型Microfacet Theory/Model
对于看向一个粗糙表面
- 宏观上:平坦且略有粗糙
- 微观上:凹凸不平,且每个微元都认为只发生镜面反射
总之,要有这么一个概念:从近处看能看到不同的几何细节,拉远后细节消失
为什么会发生漫反射?因为粗糙的物体表面在微观上可以看成超级多细小的镜子,他们的朝向/法线各不相同,他们会把光线反射到四面八方.
微表面的BRDF:
对于glossy毛面的材质,微表面的法线方向其实差不多,

把他们的分布画出来,会集中在宏观的法线周围(宏观即不看微表面,镜头拉远后忽略细节,法线正直朝上)
对于特别粗糙的材质,微表面法线分布图(左),渲染效果(右)

所以,通过微表面理论,我们可以把表面的粗糙程度用 微表面的法线分布 来表示
- 如果微表面法线分布集中 ==> glossy
- 如果微表面法线分布分散 ==> diffuse
4.2 微表面的 BRDF (双向反射分布函数 f(i,o))
注意:微观上对于表面任意一个点来说,是镜面反射

- F(i,h):Fresnel Term 菲涅尔项。给定入射方向 ωi 和半程向量h方向,返回反射方向的反射率,值域[0,1]
- D(h) :Distribution of normals 微表面的法线分布。给定一个半程向量h,返回法线位于该方向的微表面数量
- G(i,o,h):Shadowing Masking Term 阴影遮蔽,也叫几何项。 当入射光以非常平(Grazing Angle 掠射角度)的射向表面时,有些凸起的微表面就会遮挡住后面的微表面。这一项其实就起修正作用,当入射为掠射角度时,这一项可能就会返回一个比较小的数比如0.5,0.4之类的,把BRDF的返回值拉低一点。 如果没有这一项,假如我们渲染一个球,球的边界上,就会是掠射角度,会特别亮。(看分子 菲涅尔项F(i,h) 返回值接近1,D(h)的返回值也会很大,因为微表面法线分布基本是正态分布,又因为入射很平,半程向量很居中,微表面的数量是最多的,返回值就大。最终就造成BRDF返回值比较大,反射光的能量只会减少很少的两,因此边缘着色特别亮。)
4.3 微表面模型渲染出来的效果特别真实

现在特别火的PBR——physically Based Rendering 就一定会使用微表面模型。为了更好的效果和表现,工业界有很多自己开发的不同种类的微表面模型,但是都是基于上面介绍的微表面模型搞出来的 核心是不变的。
五、 各向同性/异性材质
电梯间的四周的材质是这种沿某方向磨过的金属,它的高光表现如下所示,这是种各项同性材质。

- Isotropic Material:各向同性材质,各个方向法线分布是差不多的,方向性很弱。
- Anisotropic Material:各项异性材质,各个方向法线分布是不同的,方向性很强。如沿着某个方向刷过的金属

这两种BRDF的区分方式:
各向同性材质:BRDF值只跟相对方位角有关,BRDF函数可以从四维降成三维
什么意思?—— 对于各向同性材料,不管入射方位角 φi ,和出射方位角 φr ,怎么变化,只要这俩角度的相对差值 |φi - φr| 没变,那BRDF就不变,加绝对值是因为光的可逆性,下面公式也可以加上问题不大。
具体来说,入射方向和出射方向的方位角同时绕着色点随便怎么转,只要 |φi - φr| 不变,BRDF返回值不会变,着色结果相同。

各项异性材质:绝对方位角(各自的φ)有关,只要任意一方的方位角改变,就会呈现比较大的差别。

六、 BRDF的性质总结
(1) 非负性:fr(ωi ->ωr ) ≥ 0
(2)线性:BRDF可以分成多项分别计算后相加(类似Blinn-Phong模型分成高光+漫发射+环境光)

(3)可逆性:调换BRDF的入射光和出射光,返回值是一样的

(4)能量守恒:不能违背能量守恒原则。下面公式,其实可以看做是半球上所有方向入射光的能量Li总 的一个系数,这个系数必须满足 ≤ 1

(5)各向异性/各向同性BRDF:不管是各项同性还是异性材质都遵循光的可逆性,互换出入射光,BRDF返回值不变。
各向同性材质BRDF:跟出入射方位角无关,跟他们相对差值有关,因此四维BRDF函数变成三维。保持相对静止,方位角随便怎么旋转,BRDF返回值不变。
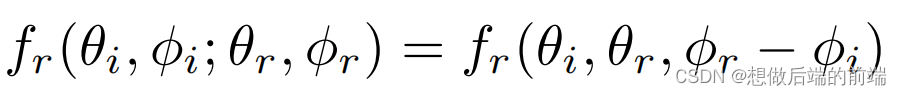
并且满足光的可逆性,交换出入射光,数值不变;方位角也不用管谁大谁小。
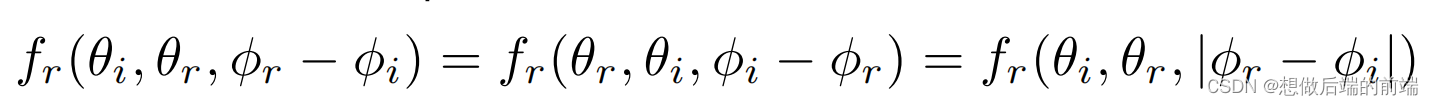
各向异性材质BRDF:跟绝对方位角有关。

)



-- colcon的使用)


)







)
—求解时滞微分方程(1))


