动态规划理论

定义

动态规划(Dynamic Programming，简称DP)，主要用于解决多阶段决策问题。它的核心思想是将一个复杂的多阶段问题转化为一系列相对简单的单阶段问题，然后逐一求解这些单阶段问题，最后将这些单阶段问题的解合并，得到原始问题的解

动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区别于贪心，贪心没有状态推导，而是从局部直接选最优的，

动态规划的主要理论基础包括最优性原理、无后效性和有重叠子问题三个性质：

• 最优性原理：如果问题的最优解所包含的子问题的解也是最优的，称该问题具有最优子结构，满足最优性原理。

• 无后效性：即某个阶段的状态一旦确定，就不受这个状态以后决策的影响。

• 有重叠子问题：即子问题之间是不独立的，一个子问题在下一个阶段决策中可能多次使用到。

在实际应用中，动态规划已被广泛应用于各类问题，如路径优化、资源分配、生产调度、库存管理和投资组合等优化问题。例如，在路径优化问题中，可以将路径划分为多个阶段，每个阶段的状态表示为路径的一部分，决策表示为选择哪条路径，然后通过动态规划算法求出最优路径。

动态规划的解题步骤

这里推荐卡哥总结的动规五步曲:

状态转移公式（递推公式）是很重要，但动规不仅仅只有递推公式。

对于动态规划问题，将拆解为如下五步曲，将五步都搞清楚，才能是把动态规划真的掌握了

1. 确定dp数组（dp table）以及下标的含义

2. 确定递推公式

3. dp数组如何初始化

4. 确定遍历顺序

5. 举例推导dp数组

这里之所以要先确定递推公式，然后在考虑初始化，是因为一些情况是递推公式决定了dp数组要如何初始化！其实 确定递推公式 仅仅是解题里的一步而已！搞不清楚dp数组应该如何初始化，或者正确的遍历顺序，以至于记形忘神。

写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。对于结果的处置，这就要说到非常重要的的debug；把dp数组打印出来，看看究竟是不是按照正确思路推导的，这样可以才能更好的修改逻辑.

算法题

Leetcode 509. 斐波那契数

题目链接:509. 斐波那契数

 大佬视频讲解：斐波那契数视频讲解

 个人思路

熟悉的课后题，递推公式题目就直接给了，只用初始化数值，然后遍历即可；

解法

动态规划

虽然是道简答题，也要好好分析直至慢慢掌握动规。

动规五部曲：

用一个一维dp数组来保存递归的结果

1.确定dp数组以及下标的含义

dp[i]的定义为：第i个数的斐波那契数值是dp[i]

2.确定递推公式

题目已经把递推公式直接出：状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];

3.dp数组如何初始化

题目中把如何初始化也直接给出了：

dp[0] = 0;
dp[1] = 1;

4.确定遍历顺序

从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，那么遍历的顺序一定是从前到后遍历的

5.举例推导dp数组

按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2]，推导一下当N为10的时候，dp数组应该是如下的数列：0 1 1 2 3 5 8 13 21 34 55

代码写出来可以打印一下，如果一样就ok，不一样则debug一下

class Solution {public int fib(int n) {if (n <= 1) return n;             int[] dp = new int[n + 1];dp[0] = 0;//初始化dp[1] = 1;for (int index = 2; index <= n; index++){//遍历dp[index] = dp[index - 1] + dp[index - 2];//递推公式}return dp[n];}
}

时间复杂度:O(n)；（遍历n个数）

空间复杂度:O( n);（存储一个长度为n+1的dp数组）

---

 Leetcode  70. 爬楼梯

题目链接:70. 爬楼梯

大佬视频讲解：爬楼梯视频讲解

个人思路

和上一题有些相像，递推公式也是一样的，所以也是很快就能解决；o.O先找找动规做题自信

解法

动态规划

动规的题目如果一眼看不出规律，就多举几个例子就行；

比如：爬到第一层楼梯有一种方法，爬到二层楼梯有两种方法。那么第一层楼梯再跨两步就到第三层 ，第二层楼梯再跨一步就到第三层。所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来，那么就可以想到动态规划了。

动规五部曲：

定义一个一维数组来记录不同楼层的状态

1.确定dp数组以及下标的含义

dp[i]： 爬到第i层楼梯，有dp[i]种方法

2.确定递推公式

从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。

首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。

还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。

那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！所以dp[i] = dp[i - 1] + dp[i - 2] 。

在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。这体现出确定dp数组以及下标的含义的重要性！

3.dp数组如何初始化

需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况。所以本题其实就不应该讨论dp[0]的初始化！

所以dp[1] = 1，dp[2] = 2，然后从i = 3开始递推

4.确定遍历顺序

从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的

5.举例推导dp数组

举例当n为5的时候，dp table（dp数组）应该是这样的

与斐波那契数列唯一的区别是dp[0]在本题没有意义！

public int climbStairs(int n) {int[] dp = new int[n + 1];dp[0] = 1;//初始化dp[1] = 1;for (int i = 2; i <= n; i++) {//遍历dp[i] = dp[i - 1] + dp[i - 2];//地推公式}return dp[n];
}

时间复杂度:O(n)；（遍历n个数）

空间复杂度:O( n);（存储一个长度为n+1的dp数组）

---

 Leetcode  746. 使用最小花费爬楼梯

题目链接:746. 使用最小花费爬楼梯

大佬视频讲解：使用最小花费爬楼梯视频讲解

个人思路

这道题加了个花费体力值，那在递推时就要考虑1,2步内选择体力最小的情况累加。

解法

动态规划

1.确定dp数组以及下标的含义

dp[i]的定义：到达第i台阶所花费的最少体力为dp[i]。

2.确定递推公式

可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。

dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。

dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。

选最小的，所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

3.dp数组如何初始化

看一下递归公式，dp[i]由dp[i - 1]，dp[i - 2]推出，那么需要初始化dp[0]和dp[1]就够了，其他的最终都是dp[0]dp[1]推出。

因为题目说是从 下标 0 下标1 开始跳，初始化 dp[0] = 0，dp[1] = 0;

4.确定遍历顺序

因为dp[i]由dp[i-1]dp[i-2]推出，所以是从前到后遍历cost数组

5.举例推导dp数组

拿示例2：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ，来模拟一下dp数组的状态变化，如下：

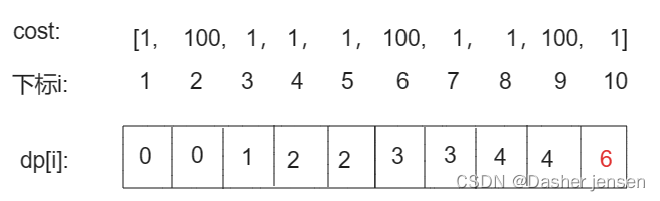
class Solution {public int minCostClimbingStairs(int[] cost) {int len = cost.length;int[] dp = new int[len + 1];//dp数组// 从下标为 0 或下标为 1 的台阶开始，因此支付费用为0dp[0] = 0;dp[1] = 0;// 计算到达每一层台阶的最小费用for (int i = 2; i <= len; i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[len];}
}

时间复杂度:O(n)；（遍历cost数组长度）

空间复杂度:O( n);（额外的dp数组来存储中间结果）

---

 以上是个人的思考反思与总结，若只想根据系列题刷，参考卡哥的网址代码随想录算法官网