微服务之分布式事务概念

CAP定理和Base理论

CAP定理

CAP定理在1998年被加州大学的计算机科学家 Eric Brewer 提出，分布式系统有三个指标：

• 一致性（Consistency）
• 可用性（Availability）
• 分区容错性（Partition Tolerance）
  Eric Brewer认为分布式系统无法同时满足这三个指标，这个结论就叫CAP定理。

一致性指的是用户访问分布式系统中的任何一个节点，得到的数据必须一致。即需要考虑分布式系统中的节点如何进行数据同步。

可用性是用户访问任意一个健康的节点，必须能得到响应，而不是超时或者拒绝。

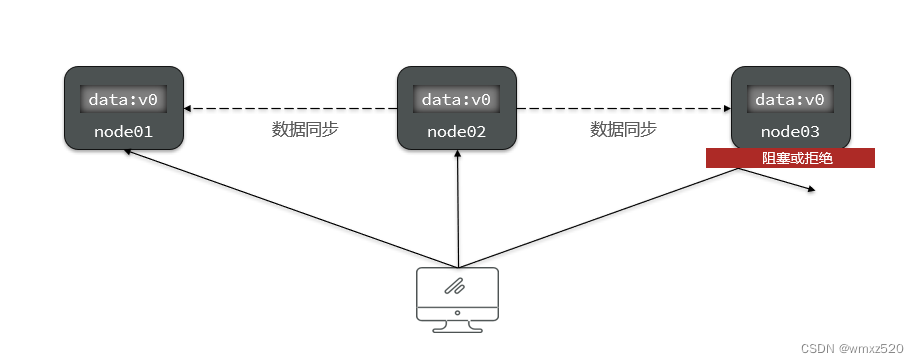
分区容错性中的分区指的是是当系统因为网络故障或者某个节点与其它节点失去连接，而形成独立分区时。容错性指的是在集群中出现分区时，整个系统也要能够持续对外提供服务。

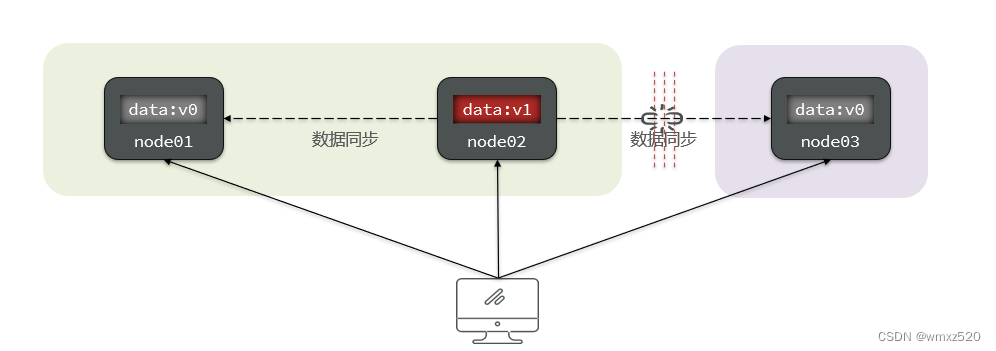
总结一下：分布式系统一定要满足分区容错性，如果不能满足分区容错性，那就和单体系统没有区别了，一旦出现问题，整个系统就不可用了。
分布式系统一定会出现分区问题，即P，这个时候不可能同时满足C和A。

Base理论

Base理论是对CAP的一种解决思路，它包含三个思想：

• 基本可用：分布式系统出现故障时，允许损失部分可用性，即保证核心可用
• Soft State：在一定时间内，允许出现中间状态，比如临时的不一致状态；
• 最终一致性：虽然无法保证强一致性，但是在中间状态结束后，最终达到数据一致性。

分布式事务最大的问题是各个子事务的一致性问题，因此可以借鉴CAP定理和BASE理论：

• AP模式：各子事务分别执行提交，允许出现结果不一致，然后采用弥补措施恢复即可，实现最终一致性
• CP模式：各个子事务执行后互相等待，同时提交，同时回滚，达成强一致性，但事务等待过程中，处于弱可用状态。

分布式事务概念

在分布式系统下，一个业务的执行可能会跨越多个服务或者数据源，在每一个服务中的执行都是一个事务，要保证所有的事务最终状态一致，这样的事务就是分布式事务。

分布式事务模型

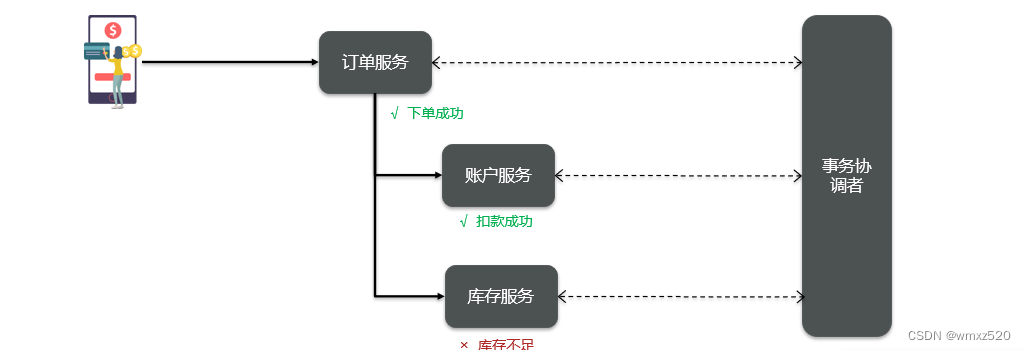
为了解决分布式事务的问题，需要各个子系统能感知到彼此事务的状态，当其中一个系统的事务出现问题时，则所有子系统全部回滚事务；如果子系统的事务没有问题，则再全部提交，这样就能保持状态一致。因此需要一个事务协调者来协调每一个事务的参与者（子系统事务）。

**

原子提交协议

原子提交协议是一种分布式事务处理协议，使用这种协议可以保证分布式事务的原子性、一致性、隔离性和持久性。原子提交协议通过协调多个事务参与者，确保事务要么全部成功，要么全部失败。原子提交协议可以基于Paxos算法和基于Raft算法实现。原子提交协议也适用于分布式数据库、分布式文件系统。
常见的原子提交协议有：二阶段提交协议（2PC）和三阶段提交协议（3PC）。
原子提交协议包括两个阶段：

1. 第一阶段：在准备阶段，协调者向所有参与者发送准备消息，参与者会检查事务是否可以提交，如果可以，则进入提交阶段，否则回滚事务
2. 第二阶段：协调者根据参与者的响应决定是否提交事务

三阶段提交协议：在第一阶段和第二天阶段之间增加了一个预提交阶段，协调者根据参与者的响应决定是否进入第二阶段。

参考

1. 5种分布式事务解决方案
2. Seata官网
3. 微服务分布式事务4种解决方案实战
4. 分布式事务（二）之两阶段提交
5. Spring-Cloud-alibaba版本依赖关系