1.顺序表查找
基本方法:
设查找表以一维数组来存储,要求在此表中查找出关键字的值为x的元素的位置,若查找成功,则返回其位置(即下标),否则,返回一个表示元素不存在的下标(如0或-1)。
1.1简单顺序查找
基本思想: 遍历整个顺序表逐个比较,如果关键字相等则返回其下标,如果没有找到则返回-1。
//从左向右查找
int search (elementtype A[],keytype x) { int i;for(i = 0; i < n; i++) if (A[i].key==x)return(i);return(-1);
}//从右向左查找
int search ( elementtype A[],keytype x) {int i;for(i = n-1; i >= 0; i--) if (A[i].key == x) return(i);return(i);
}//监视哨,这里数据存放在下标1~n
int search ( elementtype A[],keytype x) {int i = n;A[0].key=x;while (A[i].key != x) i--;return(i);
}
1.2 二分查找
基本思想: 设查找区域的首尾下标分别用变量low和high表示(初值分别为0和n-1,其中数组的下标从0开始,这与简单顺序查找中略有不同),将待查关键字x和该区域的中间元素 (其下标mid的值为low和high的算术平均值,即(low+high)/2) 的关键字进行比较,并根据比较的结果分别作如下处理:
- x==A[mid].key:查找成功,返回mid的值。
- x<A[mid].key:说明待查元素只可能在左边区域(下标从low到mid-1),因此,应在此区域继续查找。
- x>A[mid].key:说明待查元素只可能在右边区域(下标从mid+1到high) ,因此,应在此区域继续查找。
若表中存在所要查找的元素,则经过反复执行上述过程可以很快地找到,并返回元素下标,否则,返回-1以表示查找失败。
//首先要把握下面几个要点:
//right=n-1 => while(left <= right) => right=middle-1;
//right=n => while(left < right) => right=middle;
//middle的计算不能写在while循环外,否则无法得到更新。 /*!
* @brief 非递归二分查找
*
* @param[in] elements:存放有序元素的数组
* @param[in] key:待查找的元素
* @param[in] size:数组的尺寸
* @return 数组中key的下标,没有则返回-1
*/
template<typename T>
int binSearch(T* elements, T key, int size) {int low = 0, high = size - 1;while (low <= high) {//计算时避免值溢出int mid = low + ((high - low) >> 1);if (elements[mid] > key) {high = mid - 1;}else if (elements[mid] < key) {low = mid + 1;}else {return mid;}}return -1;}/*!
* @brief 递归二分查找
*
* @param[in] elements:存放有序元素的数组
* @param[in] key:待查找的元素
* @param[in] low:下界
* @param[in] high:上界
* @return 数组中key的下标,没有则返回-1
*/
template<typename T>
int binSearch(T* elements, T key, int low, int high) {//递归终止条件if (low > high) {return -1;}else {//计算时避免值溢出int mid = low + ((high - low) >> 1);if (elements[mid] > key) {return binSearch(elements, key, low, mid - 1);}else if (elements[mid] < key) {return binSearch(elements, key, mid + 1, high);}else {return mid;}}
}
1.3 索引表查找
核心思想是块间有序,块内无序;首先在索引表间查找确定元素所在的块,然后在确定的块中查找;
- 块间查找:在索引表中查找既可以用简单顺序查找,也可以用二分查找;
- 块内查找:在块内查找只能用顺序查找;
1.4 算法分析
| 查找方法 | 平均查找长度 | 最坏查找长度 |
|---|---|---|
| 简单顺序查找 | (n+1)/2 | n |
| 二分查找 | l o g 2 ( n + 1 ) − 1 log_2(n+1)-1 log2(n+1)−1 | l o g 2 ( n ) + 1 log_2(n)+1 log2(n)+1 |
注:二分查找平均查找长度计算过程
2.树表查找
2.1 二叉排序树(BST树)
定义: 二叉排序树是一棵二叉树,或者为空,或者满足以下条件:
- 若左子树不空,则左子树中所有结点的值小于根结点的值;
- 若右子树不空,则右子树中所有结点的值不小于根结点的值;
- 左右子树都为二叉排序树。
/*** 非递归二叉排序树查找* * @tparam T* @param tree* @param x* @return*/
template<typename T>
Node<T> *bstsearch(Node<T> *tree, T x) {Node<T> *p = tree;while (p != nullptr) {if (p->data == x) {return p;}if (x < p->data) {p = p->lchild;} else {p = p->rchild;}}return nullptr;
}/*** 递归二叉排序树查找* * @tparam T * @param tree * @param x * @return */
template<typename T>
Node<T> *bstsearch(Node<T> *tree, T x) {if (tree == nullptr) {return tree;}if (tree->data == x) {return tree;}if (x < tree->data) {return bstsearch(tree->lchild, x);} else {return bstsearch(tree->rchild, x);}
}
二叉排序树的构造
核心:从空树出发,依次插入若干个节点;
步骤:
- 若该值小于根结点的值,则应往左子树中插入 (递归调用插入算法)。
- 若该值大于等于根结点的值,则往右子树中插入(递归调用)。
- 按此方式递归调用若干次后,总可以搜索到一个空子树位置,即要插入的位置。
/*** 在树tree中插入节点curNode* * @tparam T * @param tree * @param curNode */
template<typename T>
void insert(Node<T> *&tree, Node<T> *curNode) {if (tree == nullptr) {tree = curNode;return;}if (curNode->data < tree->data) {insert(tree->lchild, curNode);} else {insert(tree->rchild, curNode);}
}/*** 基于控制台输入,创建二叉排序树* * @tparam T * @param tree */
template<typename T>
void create(Node<T> *&tree) {tree = nullptr;int x;cin >> x;while (x != 0) {Node<int>* node = new Node(x);insert(tree, node);cin >> x;}
}
该构造方式的问题是,当输入是一个递增或者递减序列时,则该树是相当倾斜的,即左右子树的深度差距很大;
二叉排序树删除结点
删除只能和删除结点,不能删除以结点为根的子树,且还要保证删除后所得二叉树仍满足二叉排序树的性质不变。
1.被删除的结点是叶子结点:直接删去该结点。
2.被删除的结点只有右子树或者只有左子树,用其右子树或者左子树替换
3.被删除的结点既有左子树又有右子树,找到删除结点的左子树中的最大值,将其替换删除结点(或者找右子树上最小的结点)
2.2 平衡二叉树(AVL树)
定义:
平衡二叉树是一棵二叉排序树,或者为空,或者满足以下条件:
- 左右子树高度差的绝对值不大于1;
- 左右子树都是平衡二叉树。
平衡因子:
左子树的高度减去右子树的高度,其值为-1,0或1。
对于一颗有n个结点的AVL树,其高度保持在O(log2n)数量级,平均查找长度(ASL)也保持在O(log2n)量级。
如何构造平衡二叉树
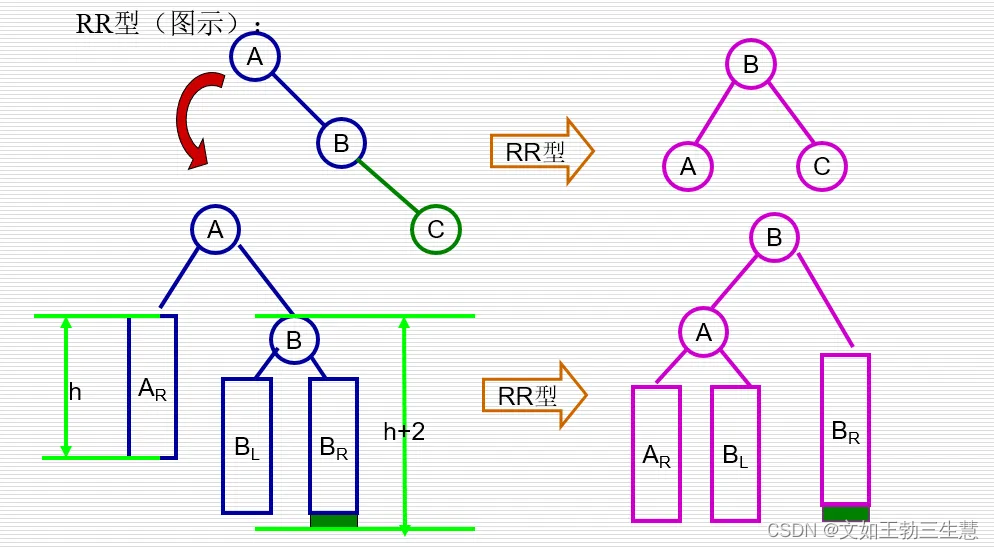
在平衡的二叉排序树中插入一个结点,当出现不平衡时,根据不平衡情况分四种调整方法
——假设最低不平衡结点为A,根据新插入结点与A的位置关系来命名调整方法:
LL型:新插入结点在A的左孩子(L)的左子树(L)中;

LR型:新插入结点在A的左孩子(L)的右子树®中;

RL型:新插入结点在A的右孩子®的左子树(L)中;
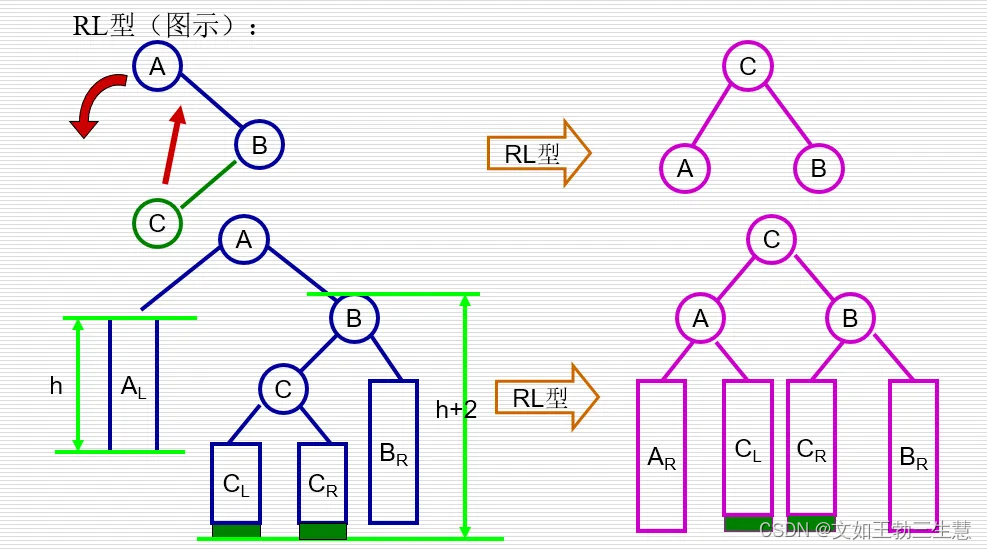
RR型:新插入结点在A的右孩子®的右子树®中。
2.3 红黑树(RBT)
红黑树(Red-Black Tree)也是是一种自平衡的二叉搜索树,与AVL树不同的是它在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍(最长路径也不会超出最短路径的两倍,因此红黑树的平衡性要求相对宽松,没有AVL树那样严格),从而使搜索树达到一种相对平衡的状态。
红黑树具有以下性质:
- 每个结点不是黑色就是红色;
- 根结点必须是黑色的
- 红色结点的两个子结点必须都是黑色的,这保证了没有两个连续的红色节点相连
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,也被称为NIL节点或者NULL节点)
- 任意结点到其每个叶子结点的简单路径上,黑色节点的数量相同:确保了树的黑平衡性,即红黑树中每条路径上黑色结点的数量一致。
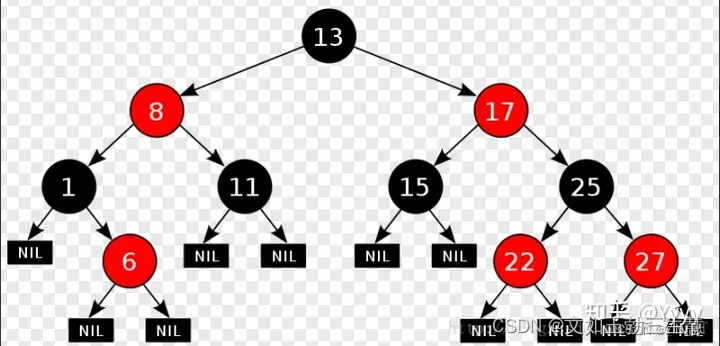
所以我们这里来分析一种极端的情况:
大家想,如果一棵红黑树有红有黑,它里面如果有一条全黑的路径,那这条全黑的路径一定就是最短路径; 如果有一条是一黑一红,一黑一红…,这样黑红相间的,那他就是最长的路径。 然后它们里面的黑色结点个数又是相同的的,所以最长路径最多是最短路径的两倍,不可能超过最短路径两倍。 所以这样红黑树的高度就能够保持在一个相对平衡的范围内,当然他就没有AVL树那么严格
红黑树的插入
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
- 按照二叉搜索的树规则插入新节点,除了根节点为黑色,新插入的节点初始为红色;
- 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整。但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树进行调整;
调整的总体思路是重新着色或者旋转+重新着色,旋转的思路跟AVL树类似,详见 https://zhuanlan.zhihu.com/p/659174741
红黑树的删除
将红黑树内的某一个节点删除,需要执行哪些步骤呢? ⑴首先,红黑树是一棵二叉查找树,按照二叉查找树的节点删除规则删除该节点;⑵然后,通过旋转和重新着色操作来修正该树的红黑树特性。详细步骤如下:
第一步:将节点按照二叉查找树的删除规则进行节点删除。
这和“删除常规二叉查找树中的节点方法是一样的”。分3种情况:
Ⅰ.被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
Ⅱ.被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
Ⅲ.被删除节点有两个儿子。那么,先找出它的[前驱节点/后继节点];然后把“它的[前驱节点/后继节点]的内容”复制给“该节点”;之后,删除“它的[前驱节点/后继节点]”。在这里,[前驱节点/后继节点]相当于替身,在将[前驱节点/后继节点]的内容复制给"被删除节点"之后,再将[前驱节点/后继节点]删除。这样就巧妙的将问题转换为“删除[前驱节点/后继节点]”的情况了,下面就考虑[前驱节点/后继节点]。在"被删除节点"有两个非空子节点的情况下,它的[前驱节点/后继节点]不可能是双子非空。既然"[前驱节点/后继节点]"不可能双子都非空,就意味着"该节点的[前驱节点/后继节点]"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况Ⅰ"进行处理;若只有一个儿子,则按"情况Ⅱ"进行处理。
查找效率分析
对于一棵红黑树来说,如果它里面全部的黑色结点一共有N个的话,那它的最短路径长度就差不多是 l o g 2 ( N ) log_2 (N) log2(N)。 然后整棵树的节点数量就是在【N,2N】之间。 所以最长路径长度就可以认为差不多是 2 l o g 2 ( N ) 2log_2 (N) 2log2(N) 所以红黑树的查找最少是 l o g 2 ( N ) log_2 (N) log2(N)次,最多是 2 l o g 2 ( N ) 2log_2 (N) 2log2(N)次,所以红黑树查找的时间复杂度是O( l o g 2 N log_2 N log2N),计算时间复杂度前面的常数项可以省略。 而AVL树也是O( l o g 2 N log_2 N log2N),但AVL树是比较严格的O( l o g 2 N log_2 N log2N),而红黑树是省略了常数项。 所以严格来说,红黑树的查找效率是比不上AVL树的(但对于计算机来说是没什么差别的),但是它们是同一个数量级的,都是O( l o g 2 N log_2 N log2N)。
红黑树对比AVL树
由于AVL树要求更加严格的平衡,所以在进行插入和删除操作时,可能需要更频繁地进行旋转操作来调整树的结构,以保持平衡。相比之下,红黑树的插入和删除操作需要旋转的次数相对较少,因此在插入和删除操作频繁的情况下,红黑树可能更加高效。
综合来看,红黑树其实更胜一筹,红黑树在实际应用中更为常用,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树实现的;
第二步:通过旋转和重新着色操作来修正该树的红黑树特性。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
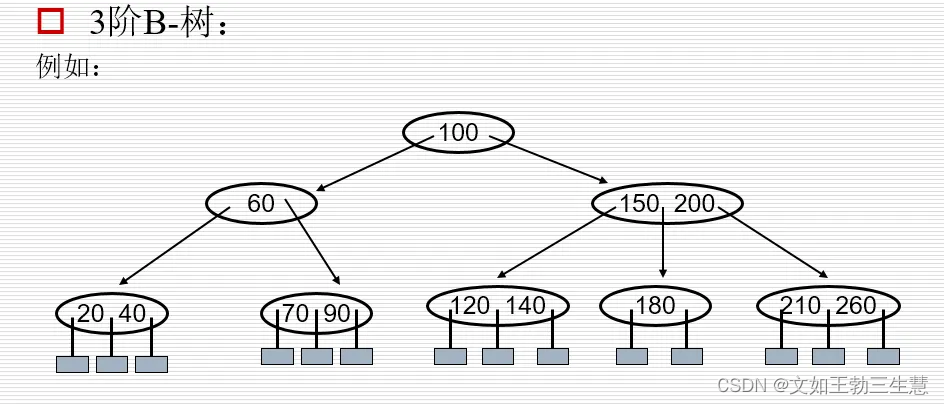
2.4 B树
注:B树有时候也会写作B-树,是一个意思;
定义:m阶B树(m≥3)满足如下条件:
- 每一个结点分支数≤m;
- 根结点分支数≥2(要求此根结点不为叶子结点);
- 其余分支结点的分支数≥ m/2 ;
- 所有叶子结点在同一层;
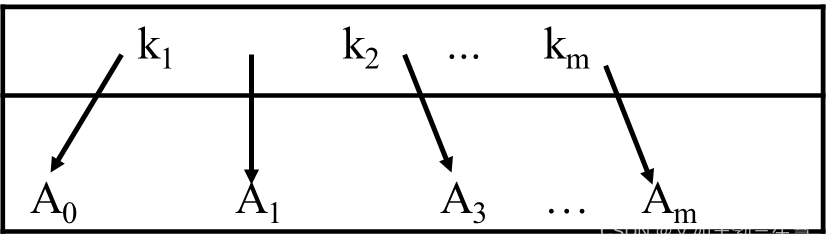
- 每一个结点的结构如下:
满足 A 0 < K 1 < A 1 < . . . < K m < A m A_0<K_1<A_1<...<K_m<A_m A0<K1<A1<...<Km<Am,其中Ai表示其中的所有关键字;
插入关键字——插入到叶子结点中
- 插入后,该结点的关键字个数 n<m, 不修改分支指针;
- 插入后,该结点的关键字个数 n=m, 则需进行“结点分裂”,令 s = m / 2 m/2 m/2, 在原结点中保留 (A0,K1,…… , Ks-1,As-1); 建新结点 (As,Ks+1,…… ,Kn,An); 将(Ks,p)插入双亲结点,p是指向新节点的指针;
3)若双亲为空,则建新的根结点。



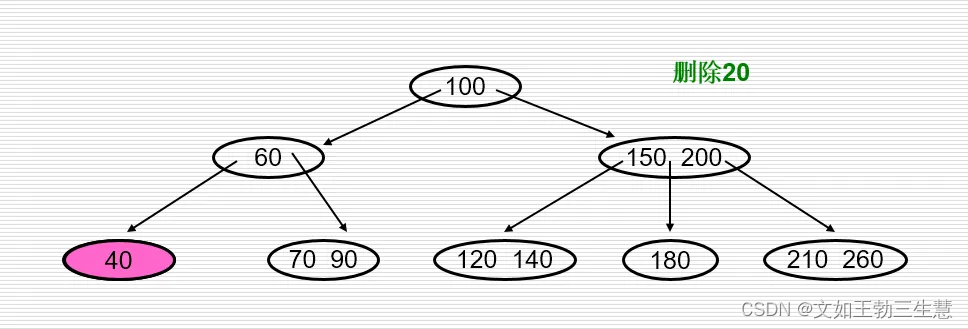
删除关键字
- 在深度为(h+l)的m阶B-树中删除一个键值k,首先要查到键值k所在的结点及在结点中的位置。若k在非叶子节点中,则把该结点的右边(或左边)指针所指子树中的最小(或最大)键值与k对调,使k移到有叶子节点。
- 在叶子节点中删除一个键值后,使得该结点的值个数n减1,此时应分以下三种情况进行处理: a.
- 若删除后结点中键值数目 n ≥ m / 2 − 1 n≥m/2-1 n≥m/2−1,在该结点中删去键值k连同右边的指针。 b.
- 若删除后结点中键值数目 n < m / 2 − 1 n<m/2-1 n<m/2−1,且左(或右)兄弟结点的关键字数目> m / 2 − 1 m/2-1 m/2−1,则把左(或右)兄弟结点中最大(或最小)键值移到父结点中,再把父结点大于(或小于)上移键值的键值下移到被删关键字所在结点中。 c.
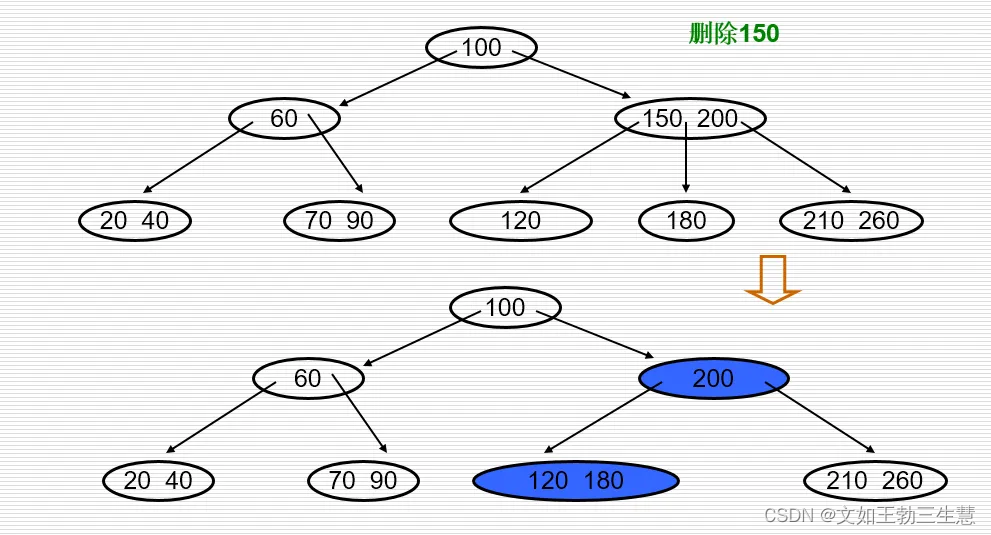
- 若删除后结点中键值数目 n < m / 2 − 1 n<m/2-1 n<m/2−1,及其左、右兄弟结点的键值数目都等于 m / 2 − 1 m/2-1 m/2−1,则就必须进行结点的“合并”,即把应删的键值删去后,将该结点中的剩余键值和指针连同父结点中指向该结点指针的左边(或右边)一个键值ki一起合并到左兄弟(或右兄弟)结点中,将ki从父结点中删去。如果因此使父结点中关键字数目< m / 2 − 1 m/2-1 m/2−1,则对此父结点做同样处理,以致于可能直到对根结点做这样的处理而使整个树减少一层。
- 如果因此使父结点中关键字数目< m / 2 − 1 m/2-1 m/2−1,则对此父结点做同样处理,以致于可能直到对根结点做这样的处理而使整个树减少一层。

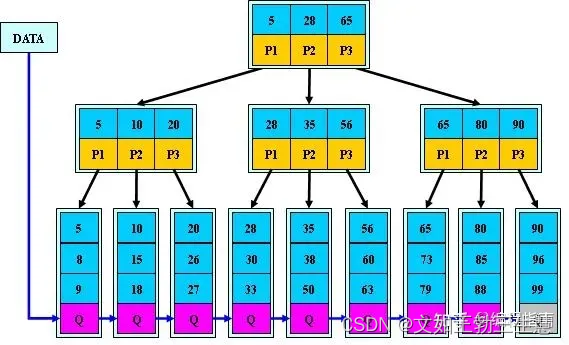
2.5 B+树
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别。
B+树是B树的变体,也是一种多路搜索树,其定义基本与B-树相同,除了:
1)非叶子结点的子树指针与关键字个数相同;
2)非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
3)为所有叶子结点增加一个链指针;
4)所有关键字都在叶子结点出现;
B+树的搜索与B树也基本相同,区别是B+树只有达到叶子结点才命中(B树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B+树的性质:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4.更适合文件索引系统。
B+树比B树更适合操作系统的文件索引和数据库索引的原因:
B+树的磁盘读写代价更低,B+树的内部节点没有指向关键字具体信息的指针,因此内部节点相对B树更小。如果把所有同一内部节点的关键字放在同一块磁盘中,盘块所能容纳的关键字数量也就越多,一次性读入内存中的需要查找的关键字也就越多,相对IO读写次数降低。
B+树的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
所以,B+树只要遍历叶子节点就可以实现整棵树的遍历,支持基于范围的查询,而B树不支持range-query这样的操作(或者说效率太低)。
2.6 B*树
B∗树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针,将结点的最低利用率从1/2提高到2/3。
B∗树定义了非叶子结点关键字个数至少为2/3M,即块的最低使用率为2/3(代替B+树的1/2);

B+树的分裂:
当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B∗树的分裂:
当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
所以,B∗树分配新结点的概率比B+树要低,空间使用率更高。
特点
在B+树的基础上因其初始化的容量变大,使得节点空间使用率更高,而又存有兄弟节点的指针,可以向兄弟节点转移关键字的特性使得B*树额分解次数变得更少。
2.5 算法分析
| 查找方法 | 平均查找长度 | 失败查找长度 |
|---|---|---|
| 二叉排序树 | l o g 2 ( n ) log_2(n) log2(n) | n |
| 二叉平衡树 | l o g 2 ( n ) log_2(n) log2(n) | l o g 2 ( n ) log_2(n) log2(n) |
| 红黑树 | l o g 2 ( n ) log_2(n) log2(n) | $ n>> x > log_2(n)$含义是略差于二叉平衡树,但是远远好于二叉排序树 |
| B树 | ≤ l o g m ( n + 1 ) + f i n d ( m ) ≤log_m(n+1)+find(m) ≤logm(n+1)+find(m) | 1 + l o g m / 2 ( ( n + 1 ) / 2 ) + f i n d ( m ) 1+log_{m/2}((n+1)/2)+find(m) 1+logm/2((n+1)/2)+find(m) find(m)指的是在m个元素中的查找长度,m一般比较小,采用顺序查找即可 |
| B+树 | l o g m ( n + 1 ) + f i n d ( m ) log_m(n+1)+find(m) logm(n+1)+find(m) | 1 + l o g m / 2 ( ( n + 1 ) / 2 ) + f i n d ( m ) 1+log_{m/2}((n+1)/2)+find(m) 1+logm/2((n+1)/2)+find(m) find(m)指的是在m个元素中的查找长度,m一般比较小,采用顺序查找即可 |
3.哈希表查找
给定关键字key,用一个函数H(key)计算出元素地址,由此而得散列表(Hash表,哈希表),
其中函数H(key)称为散列函数
此函数值称为散列地址。
现实中,会出现k1≠k2但H(k1)=H(k2)的情况,称这种现象为冲突现象,k1,k2为同义词。
针对冲突——如何解决冲突呢?
- 构造好的散列函数,以免冲突(减少冲突)
- 妥善处理冲突
构造散列函数的基本方法
直接定址法
H(k)= k 或者 H(k)= ak+b (a,b为任意正整数)
除留余数法
H(k)= k % p 其中p≤m,m为数组规模的最大质数。
平方取中法
例:325在平方后取105625中间两位作为它的散列地址。
折叠法
如 身份证号码:40104198805061532
先进行分组:340 104 198 805 061 532
冲突处理方法
开放地址法
Hi(k)=(H(k) + di ) % m,i=1,2,…,q q<=m
- 线性探测法:Hi(k)=(H(k)+i)%m,m为表的规模最大质数;
- 二次探测法:Hi(k) = ( H(k) + i2 ) % m
- 伪随机数:Hi(k) = ( H(k) + random() ) % m
拉链法
将同义词构成一个链表
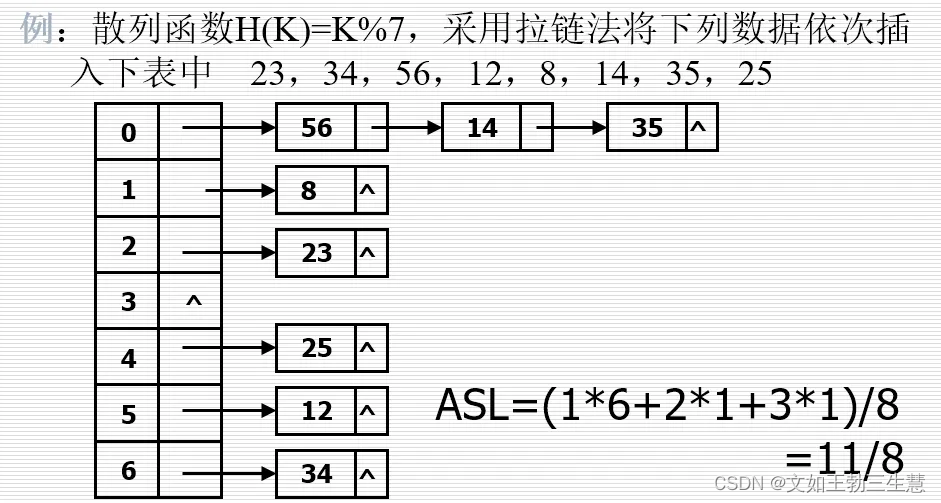
再散列法
→H(k)→H1(k)→H2(k)→ …… →Hi(k)
散列表的查找
在散列表中查找元素的过程和构造的过程基本一致:
对给定关键字k,由散列函数H计算出该元素的地址H(k)。
- 若表中该位置为空,则查找失败。
- 否则,比较关键字,若相等,查找成功,否则根据构造表时所采用的处理方法找下一个地址,直至找到关键字等于k的元素(成功)或者找到空位置(失败)为止。
一般在用拉链法构造的表中进行查找,比在用线性探测法构造的表中进行查找,查找长度要小。
3.1 算法分析
| 查找方法 | 平均查找长度 | 失败查找长度 |
|---|---|---|
| 哈希查找 | 1 | 1+m (哈希冲突用拉链法处理,命中的地址中链表长度为m) |
参考
https://www.cnblogs.com/kongxudeshenghuo/p/16174567.html
https://zhuanlan.zhihu.com/p/477346381
https://zhuanlan.zhihu.com/p/639905710
https://blog.csdn.net/Jay_fearless/article/details/119454973
https://zhuanlan.zhihu.com/p/659174741
https://zhuanlan.zhihu.com/p/666229978












)
![每日一题 --- 替换数字[卡码][Go]](http://pic.xiahunao.cn/每日一题 --- 替换数字[卡码][Go])

eval和query)



