比赛传送门
博客园传送门
c++ 模板框架
#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
#define rep(i,a,b) for (int i=a;i<b;++i)
#define per(i,a,b) for (int i=a;i>b;--i)
#define se second
#define fi first
#define endl '\n'
#define all(x) (x).begin(),(x).end()
#define pii pair<int,int>
#define pli pair<LL,int>
#define MEM(a,x) memset(a,x,sizeof(a))
#define lowbit(x) ((x)&-(x))
inline int Ls(int p){return p<<1;}
inline int Rs(int p){return p<<1|1;}
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int N=1e3+10;
inline void Solve()
{
}
int main()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endifios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int _=1;//cin>>_;while(_--){Solve();}return 0;
}
A.遗失的旋律
把加一操作和乘二操作分开看,某一个位置出现了0表示加一,后面所有出现的1都会乘2,也就是说如果用cnt表示这个0后面1的个数,它对答案的贡献就是
对于一个给定的一个字串,答案就可以写成所有0产生的贡献之和,再加上
其中cnt表示整个区间1的个数。比如 010110 就可以写成
用线段树维护区间1的个数和区间所有0对答案贡献的总和,分别用s1和s0表示。左右合并时s0就可以用左树s0乘上右树s1,再加上右树的s0。
const int N=1e5+10,M=998244353;
char s[N];
inline int qp(int a,int b)
{int res=1;while(b){if(b&1) res=1ll*res*a%M;a=1ll*a*a%M;b>>=1;}return res%M;
}
struct sg_tree{int l,r;int s0,s1;
}T[8*N];
inline void up(int p)
{T[p].s1=T[Ls(p)].s1+T[Rs(p)].s1;T[p].s0=(1ll*T[Ls(p)].s0*qp(2,T[Rs(p)].s1)%M+T[Rs(p)].s0)%M;
}
inline sg_tree up(sg_tree L,sg_tree R)
{sg_tree t;t.s1=L.s1+R.s1;t.s0=(1ll*L.s0*qp(2,R.s1)%M+R.s0)%M;return t;
}
inline void build(int p,int l,int r)
{if(l==r){T[p]={l,r,s[l]=='0',s[l]=='1'};return;}T[p]={l,r};int mid=l+r>>1;build(Ls(p),l,mid);build(Rs(p),mid+1,r);up(p);
}
inline void upd(int p,int x)
{int &l=T[p].l,&r=T[p].r;if(l>x||r<x) return;if(l==r){s[l]=!(s[l]-'0')+'0';T[p].s0=(s[l]=='0');T[p].s1=(s[l]=='1');return;}upd(Ls(p),x);upd(Rs(p),x);up(p);
}
inline sg_tree qy(int p,int l,int r)
{sg_tree t={0,0,0,0},lt=t,rt=t;if(T[p].l>r||T[p].r<l) return t;if(T[p].l>=l&&T[p].r<=r) return T[p];if(T[Ls(p)].r>=l) lt=qy(Ls(p),l,r);if(T[Rs(p)].l<=r) rt=qy(Rs(p),l,r);return up(lt,rt);
}
inline void Solve()
{int n,m;cin>>n>>m>>s+1;build(1,1,n);while(m--){int op,x,l,r;cin>>op;if(op==1){cin>>x;upd(1,x);}else{cin>>x>>l>>r;sg_tree t=qy(1,l,r);cout<<(t.s0+1ll*x*qp(2,t.s1)%M)%M<<endl;}}
}B.时间的礼物
有很多方法可以求得方案数为:
首先可以将整数划分问题转换为隔板法问题:有n个球,m-1个隔板方案相当于是把n个数分解为m个大于0的数方案,题目要求可以等于0,n个球的左右两边可以插入隔板,这里可以增加两个球,对于隔板并在一起的情况可以在隔板之间插入球,增加了m-2个球,等价于n+m个球插入m-1个隔板的方案数,所以总方案数为:
从另外一个角度,考虑整数划分方案中0的个数为i,剩下的相当于是n个球,插入m-i-1个隔板方案数,总方案可以表示成,这个式子也等价于共有m+n-1个球,先从前面m个中选择i个,再从后面的n-1个球中选择m-i-1个,一共选择m-1个球。这个方案数也等价于直接在n+m-1个球中选m-1个方案数。
直接计算可能会存在逆元不存在的情况,可以先用素数筛找出内的素数(式子中m+n数量级可能会达到2e6),可以计算每个素数在阶乘中出现的次数,进一步算出每个素数在答案中的阶乘。
const int N=2e6+10;
int n,m,p;
int cnt,pr[N];
bool st[N];
inline void INIT()
{rep(i,2,N){if(!st[i]) pr[++cnt]=i;for(int j=1;j<=cnt&&i*pr[j]<=N-1;++j){st[i*pr[j]]=1;if(i%pr[j]==0) break;}}
}
inline int Qp(int a,int b)
{int res=1;while(b){if(b&1) res=1ll*res*a%p;a=1ll*a*a%p;b>>=1;}return res%p;
}
inline int Cal(int a,int b)
{int res=0;while(a){res+=a/b;a/=b;}return res;
}
inline void Solve()
{INIT();cin>>n>>m>>p;int ans=1;rep(i,1,cnt+1){int t=Cal(n+m-1,pr[i])-Cal(m-1,pr[i])-Cal(n,pr[i]);ans=1ll*ans*Qp(pr[i],t)%p;}cout<<ans<<endl;
}C.财政大臣
用一个数组记录变化的值,修改只需要改变单个点的值,最后从根节点做一遍dfs,记录前面节点变化值的和加到子节点上。最后答案就是变化的值加上初始的值。
const int N=1e5+10,M=2*N;
int h[N],e[M],ne[M],idx;
int a[N];
LL b[N];
inline void add(int a,int b)
{e[++idx]=b;ne[idx]=h[a];h[a]=idx;
}
void dfs(int u,int fa,int s)
{for(int i=h[u];i;i=ne[i]){int v=e[i];if(v==fa) continue;dfs(v,u,b[u]+s);}b[u]+=s;
}
inline void Solve()
{int n,m;cin>>n>>m;rep(i,0,n-1){int a,b;cin>>a>>b;add(a,b);add(b,a);}rep(i,1,n+1) cin>>a[i];while(m--){int op,u,x;cin>>op>>u>>x;if(op==1) b[u]+=x;else b[u]-=x;}dfs(1,0,0);rep(i,1,n+1) cout<<a[i]+b[i]<<" ";
}
D.实验室有多少人
用数对维护信息,开始时间对应1,表示增加1个人,结束时间对应-1,表示减少一个人。把所有数对按时间从小到大排序,相同时间的把-1的放在前面,最后遍历更新答案即可。
const int N=1e6+10;
pii a[2*N];
inline void Solve()
{int n,x,y,m=0;cin>>n;rep(i,0,n){cin>>x>>y;a[++m]={x,1};a[++m]={y,-1};}sort(a+1,a+1+m);int ans=0,nw=0;rep(i,1,m+1){nw+=a[i].se;ans=max(ans,nw);}cout<<ans<<endl;
}
E.在雾中寻宁静
先对树做一遍dfs,记录节点进入的时间L和出去的时间R,L到R就包含了该节点以及其子树节点(dfs序)。
问题转换为区间染色,因为后面的染色会覆盖前面的染色,可以考虑逆向操作,每一次只染没有染过色的点,跳过已经染过色的点。可以用并查集维护下一个未染色的点。
代码说明:
- a数组表示dfs序。
- L[i]和R[i]分别表示进入和出去时刻。
- s[i]表示i指向下一个没有填色的位置。
const int N=2e5+10,M=2*N;
int h[N],e[N],ne[N],idx;
int a[M],L[N],R[N];
int n,cnt,s[M];
pii op[N];
inline void add(int a,int b)
{e[++idx]=b;ne[idx]=h[a];h[a]=idx;
}
void dfs(int u)
{L[u]=++cnt;for(int i=h[u];i;i=ne[i]) dfs(e[i]);R[u]=++cnt;
}
int Find(int u)
{if(s[u]==u) return u;else return s[u]=Find(s[u]);
}
inline void Solve()
{cin>>n;rep(i,1,n){int x;cin>>x;add(x,i+1);}dfs(1);int q;cin>>q;rep(i,0,q){int x,y;cin>>x>>y;op[i]={x,y};}rep(i,1,2*n+2) s[i]=i;per(i,q-1,-1){int l=L[op[i].fi],r=R[op[i].fi],c=op[i].se;for(int k=Find(l);k<=r;k=Find(k)){a[k]=c;s[k]=Find(k+1);}}rep(i,1,n+1) cout<<a[L[i]]<<" ";
}
F.不规则的轮回
注意到x,y的规模不大,对n个数对暴力求出所有数对最多枚举左右,时间上可以接收,空间上只需要存储询问中的数对,然后计算出的数对在询问中就算上贡献,c++用map即可。
const int N=2e3+10;
pii a[N],b[N];
inline void Solve()
{int n,m;set<pii>q;map<pii,int>mp;cin>>n;rep(i,0,n) cin>>a[i].fi>>a[i].se;cin>>m;rep(i,0,m) cin>>b[i].fi>>b[i].se,q.insert({b[i].fi,b[i].se});rep(i,0,n){int &x=a[i].fi,&y=a[i].se;while(x!=y){if(q.count({x,y})) ++mp[{x,y}];if(x>y) x-=y;else y-=x;}if(q.count({x,y})) ++mp[{x,y}];}rep(i,0,m) cout<<mp[{b[i].fi,b[i].se}]<<endl;
}
G.完美数字
根据算术基本定理将数字分成素数乘积,除了素数2和5结合对末尾0有贡献,其他素数乘积都不会产生新的末尾0,末尾的0个数就取决于2的幂次和5的幂次中较小的一个。
将每个数2的幂次和5的幂次计算出来,分别求前缀和。然后枚举左端点 L,找到第一个较小的段和大于等于 k 的右端点 R,对答案产生 n-R+1 的贡献。注意到 L 往右移动时,R 只能右前移,不能回退(双指针算法)。
const int N=2e5+10;
int a[N],b[N];
inline int A(int x,int k)
{int rt=0;while(x%k==0){x/=k;++rt;}return rt;
}
inline void Solve()
{int n,m;cin>>n>>m;rep(i,1,n+1){cin>>a[i];b[i]=A(a[i],2);a[i]=A(a[i],5);}rep(i,1,n+1) a[i]+=a[i-1],b[i]+=b[i-1];LL ans=0;int r=1;rep(l,1,n+1){while(r<=n&&min(a[r]-a[l-1],b[r]-b[l-1])<m) ++r;if(r<=n) ans+=n-r+1;}cout<<ans<<endl;
}
H.春天与花儿
如果只改变一个数,将 ai 加到 k 的倍数即可。
对于 k=4 的情况,还有可能是把两个不同的数加到能被2整除。
对于 k=6 的情况,还有可能是把一个数加到能被2整除,另外一个加到能被3整除。
const int N=1e6+10;
int a[N],n,b[N];
inline int calc(int x,int k)
{return (k-x%k)%k;
}
inline pii Find01(int *a)
{int m1=100,m2=100;rep(i,0,n){if(a[i]<=m1){m2=m1;m1=a[i];}else if(a[i]<m2) m2=a[i];}return {m1,m2};
}
inline int Find0(int *a)
{int pos=0;rep(i,1,n){if(a[i]<a[pos]){pos=i;}}return pos;
}
inline void Solve()
{int k,ans=6;cin>>n>>k;rep(i,0,n){cin>>a[i];ans=min(ans,calc(a[i],k));}if(k==4&&n!=1){rep(i,0,n) a[i]=calc(a[i],2);auto rt=Find01(a);ans=min(ans,rt.fi+rt.se);}if(k==6&&n!=1){rep(i,0,n) b[i]=calc(a[i],3),a[i]=calc(a[i],2);int p1=Find0(a),p2=Find0(b);if(p1!=p2){ans=min(ans,a[p1]+b[p2]);}else{auto r1=Find01(a),r2=Find01(b);ans=min({ans,r1.fi+r2.se,r1.se+r2.fi});}}cout<<ans<<endl;
}
I.孤独与追求
为了避免偶数回文串的情况,先对原字符串做填充处理。然后枚举中点,可以用二分长度+字符串哈希求出以这个点为中点的最长回文串。预处理出值的前缀和数组a,根据回文串对称性,对于中点是 m,右端点是 r 的回文串,只需要求出,用线段树维护区间最大值即可。
const int N=2e6+10;
int n,mp[27];
char s[N];
LL a[N];
ULL h[N],rh[N],p[N];
namespace Segment_tree{struct sg_tree{int l,r;LL mx;};inline void up(sg_tree *t,int p){t[p].mx=max(t[Ls(p)].mx,t[Rs(p)].mx);}inline void Build(sg_tree *t,LL *a,int p,int l,int r){t[p]={l,r};if(l==r){t[p].mx=a[l];return;}int mid=l+r>>1;Build(t,a,Ls(p),l,mid);Build(t,a,Rs(p),mid+1,r);up(t,p);}inline LL Qy(sg_tree *t,int p,int l,int r){if(t[p].l>r||t[p].r<l) return -1e18;if(t[p].l>=l&&t[p].r<=r) return t[p].mx;LL res=-1e18;if(t[Ls(p)].r>=l) res=max(res,Qy(t,Ls(p),l,r));if(t[Rs(p)].l<=r) res=max(res,Qy(t,Rs(p),l,r));return res;}
}
namespace Str_Algorithm{ULL Str_Hash(char *s){ULL p=131,h=0;int n=strlen(s);rep(i,0,n) h=h*p+s[i];return h;}ULL Str_Hash(string s){ULL p=131,h=0;rep(i,0,s.size()) h=h*p+s[i];return h;}void Build_lhash(char *s,ULL *h){int n=strlen(s+1);int p=131;h[0]=0;rep(i,1,n+1) h[i]=h[i-1]*p+s[i];}void Build_lhash(string s,ULL *h){int n=s.size()-1;int p=131;h[0]=0;rep(i,1,n+1) h[i]=h[i-1]*p+s[i];}void Build_rhash(char *s,ULL *h){int n=strlen(s+1);int p=131;h[n+1]=0;per(i,n,0) h[i]=h[i+1]*p+s[i];}void Build_rhash(string s,ULL *h){int n=s.size()-1;int p=131;h[n+1]=0;per(i,n,0) h[i]=h[i+1]*p+s[i];}ULL Get_lhash(int l,int r,ULL *h,ULL *p){return h[r]-h[l-1]*p[r-l+1];}ULL Get_rhash(int l,int r,ULL *h,ULL *p){return h[l]-h[r+1]*p[r-l+1];}void Manacher(char *s,int *p,int n){int r=0,c;rep(i,1,n){if(i<r) p[i]=min(p[(c<<1)-i],p[c]+c-i);else p[i]=1;while(s[p[i]+i]==s[i-p[i]]) ++p[i];if(p[i]+i>r) r=p[i]+i,c=i;}}
}
inline void Init(char *s,int &n)
{per(i,n,0) s[2*i-1]=s[i];n=2*n-1;for(int i=2;i<=n;i+=2) s[i]='z'+1;
}
Segment_tree::sg_tree T[4*N];
inline void Solve()
{using namespace Str_Algorithm;using namespace Segment_tree;cin>>n;rep(i,0,26) cin>>mp[i];cin>>s+1;Init(s,n);rep(i,1,n+1) a[i]=a[i-1]+mp[s[i]-'a'];p[0]=1;Build(T,a,1,1,n);rep(i,1,n+1) p[i]=p[i-1]*131;Build_lhash(s,h);Build_rhash(s,rh);LL ans=-1e18;rep(i,1,n+1){int l=0,r=min(n-i,i-1);while(l<r){int mid=l+r+1>>1;if(Get_lhash(i-mid,i,h,p)==Get_rhash(i,i+mid,rh,p)) l=mid;else r=mid-1;}ans=max(ans,2*(Qy(T,1,i,i+l)-a[i])+mp[s[i]-'a']);}cout<<ans<<endl;
}
J.最后的星光
如果用两个字符串相同位置个数来表示一个状态,最终状态就是字符串长度 n,发现问题转换成广搜。
如果当前状态是 t ,采用第一种方法可以枚举选了 i 个相同的位置,状态就转移到了 t-i+m-i。注意需要满足不相等的位置足够选:。采用第二种方法,假设在相等的位置中有 i 个在 a 中,j 个在 b 中,相同位置增加了a-i个,又减少了j个,状态转移到了 t+a-i-j。直接枚举 i+j 的值,上界就是
,下界要保证不相等的位置足够选:
时间复杂度为
const int N=2010;
char s1[N],s2[N];
int d[N];
inline void Solve()
{int a,b,m;cin>>s1>>s2>>a>>b>>m;int n=strlen(s1),ct=0;rep(i,0,n) if(s1[i]==s2[i]) ++ct;MEM(d,-1);d[ct]=0;queue<int>q;q.emplace(ct);while(q.size()){int t=q.front();q.pop();rep(i,max(0,m-n+t),t+1){if(t+m-2*i<0) break;if(d[t+m-2*i]==-1){q.emplace(t+m-2*i);d[t+m-2*i]=d[t]+1;}}rep(i,max(0,a+b-n+t),min(t,a+b)+1){if(t+a-i<0) break;if(d[t+a-i]==-1){q.emplace(t+a-i);d[t+a-i]=d[t]+1;}}}cout<<d[n]<<endl;
}
K.天使的拼图
结论是矩形满足3|n且4|m,或12|n且m>=7都合法,其中n,m可以互换。
假设n是行,m是列,由于n,m可交换,下面证明只说明一种。
考虑把两个Tenshi图块拼在一起,覆盖要求中间不能有空,只有两个拼法:
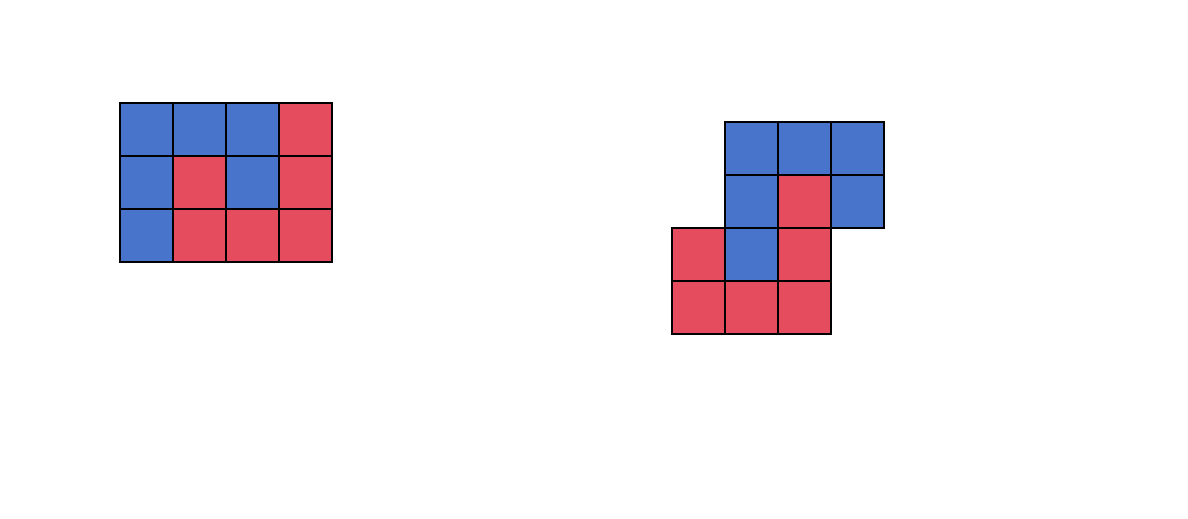
由于其他的拼法会导致中间有空隙不合法,问题就可以转换用上面两种图形经过旋转翻转覆盖矩形。
两个图形都是12块单位,如果能覆盖则一定有 12|nm
分类讨论:
- 3|n且4|m,此时显然能被上面第一个3 * 4的矩形图覆盖。
- 12|n,3|m或者4|m同1。下面考虑12|n,3和4都不能整除m,由上面两个图可知m>=3,得到m>=5。可验证m=5的情况无法覆盖。对于其他情况,如果m=3k+4,k>=1,使用第一个图,可以先把第一个3 * 4的图先横着放满,这时m=3k,后面都竖着放。如果m=3k+8,k>=1,横着放两次m就变成了 3k,也可以覆盖。
- 12|mn,m和n都不能被4整除。可知m和n都必须是偶数。将n * m的矩形分成单位正方形,将行和列分别标上号码1,2,…,n及1,2,…,m。给单位正方形(i,j)按如下方式赋值:值为i,j中能被4整除的数的个数(因此值可以为0,1,2)。这样所有的方格数字之和是偶数:考虑某个行i能被4整除产生贡献为m,对于能被4整除的列产生贡献为n,而m和n都是偶数。按照这个方法写一个程序打表,可以发现两个图不管如何放,贡献都是奇数。所以覆盖图形的个数也是偶数个,就有24|mn,则8|mn,m,n都为偶数,一定有一个被4整除,与前提矛盾,这种情况不存在。
bool ok(LL n,LL m)
{if(n%3==0&&m%4==0) return true;if(n%12==0&&m>=7) return true;return false;
}
inline void Solve()
{LL n,m;cin>>n>>m;if(ok(n,m)||ok(m,n)) cout<<"Yes"<<endl;else cout<<"No"<<endl;
}
L.擅长搞事的高木同学
如下图所示,假设要从A点走到对角E点。首先可以发现A到E最后一定是偶数步,且至少4步。
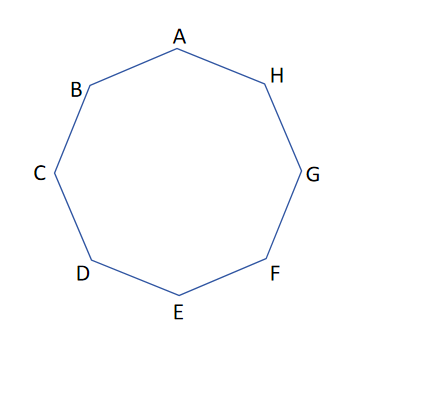
用 ,分别表示点 A,C,G到E的方案数。
注意到对称性,可知
我们可以对 进行划分,从A开始走两步,可以到达A,C,G,于是有了下式(注意到达A是A->B->A和A->H->A两种不同的走法):
再对 进行划分,从C开始走两步,可以到达C,A,于是有了下式:
边界:
写成矩阵形式用快速幂即可:
const int N=1e3+10,M=1e9+7;
struct mat{int a[2][2];mat operator*(const mat& b) const{mat c={0,0,0,0};rep(i,0,2) rep(j,0,2) rep(k,0,2) c.a[i][j]+=1ll*a[i][k]*b.a[k][j]%M,c.a[i][j]%=M;return c;}
};
inline int Qp(LL n)
{mat res={1,0,0,1},A={2,2,1,2},a={0,0,1,0};while(n){if(n&1) res=res*A;A=A*A;n>>=1;}res=res*a;return res.a[0][0]%M;
}
inline void Solve()
{LL n;cin>>n;if((n&1)||n<=3){cout<<0<<endl;}else cout<<Qp(n/2-1)<<endl;
}
M.Monika's game
用f(n)表示n的最大值。无论用什么策略,最大值始终是
证明:
对于n=1该式子成立。
对于,假设比n小的规模都满足上式,则有:
故对于,上式也成立。
inline void Solve()
{int n;cin>>n;cout<<1ll*n*(n-1)/2<<endl;
}

-COOPERATIVE_MODE)
)









)

---【链接美化、浮动布局、三种定位】)




