前言

拓扑排序是一种针对“有向无环图”的算法，用于解决一些有“依赖关系”的问题。

拓扑排序保证了当处理到某个电时，其所有的如电都已经处理过了。

例如右边这个图，拓扑序可以保证处理点2之前，点4和点6都处理过了、处理点3之前，点2和点6都处理过。

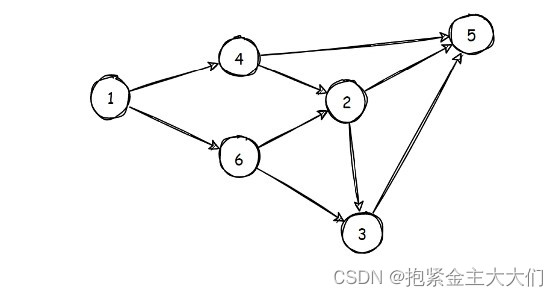
 拓扑排序不一定是“唯一”的，只要满足拓扑关系即可

以下是一些上图中的可能拓扑序：

[1,4,6,5,7,3]

[7,1,4,6,2,3,5]

[7,1,6,4,2,5,3]

,,,,

我们可以发现每个点的左侧包含它的所有入点

拓扑排序一般借助queue(队列)，使用类似BFS实现

先处理出每个点的入度，这个在读入边的时候处理。图一般用邻接表建立

for(int i=0;i<m;i++){int x=scan.nextInt();int y=scan.nextInt();list[x].add(y);f[y]++;
}
Queue<Integer> q=new LinkedList<>();
for(int i=1;i<=n;i++){if(f[i]==0){//入度为0直接加入队列q.add(i);}
}
while(!q.isEmpty()){int x=q.poll();for(int y:list[x]){if(f[y]==0)//判断Y是否入度为零，为零表示Y的入点已经处理完成了，Y可以入队q.add(y);    }
}

拓扑和动态规划的结合

在枚举X->Y的时候，可以进行状态转移，于是可以和动态规划结合起来。这样的DP也叫做DAG-DP(有向无环图上的动态规划)

状态转移一般只发生在枚举所有边的时候。

Queue<Integer> q=new LinkedList<>();
for(int i=1;i<=n;i++){if(f[i]==0)q.add(i);
}
while(!q.isEmpty()){
//进行dp转移int x=q.poll();for(int y:list[x]){f[y]--;//处理之后判断Y的入度是否为零if(f[y]==0)q.add(y);}
}

例题

给定一个n个点，m条边的有向无环图，小明从入度为0点出发，顺着边最远能走多远，若不存在这样的点，输出0

输入描述

第一行输入一个n,m

接下来m行，每行输入两个整数u,v代表有一条有向边从u到v

输出描述

输出一个整数 表示最长距离

输入输出样例

示例

输入

2 1

1 2

输出

1

（答案后期更新）