机器学习定义

机器学习就是机器通过不断训练数据集从逐渐知道正确的结果

机器学习包括监督学习和非监督学习

• 监督学习：需要输入数据和结果数据来不断训练学习

监督学习包括回归和分类
回归是结果是连续的，不是有限的
分类是结果是离散的，是有限的

非监督学习：只需要输入数据来学习
例如聚类（将某类输入数据分一组，另外一类数据分一组）

监督学习之线性回归

线性回归：就是根据一组输入数据和输出数据的对应关系进而得到当输入数据为其他时依然能得到可靠输出数据的函数关系（函数是直线的）

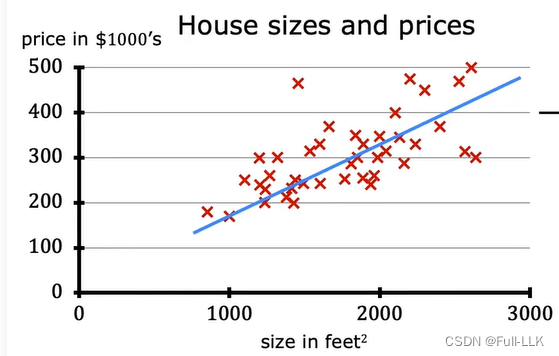
如上图通过一些关于面积和价格的数据集得到这两个之间线性关系

损失函数及可视化

损失函数即cost function
这里m是数据集的个数
可以发现通过损失函数的定义发现如果损失函数的值越小那么对应的Model函数与真实数据集的数据对应关系越接近

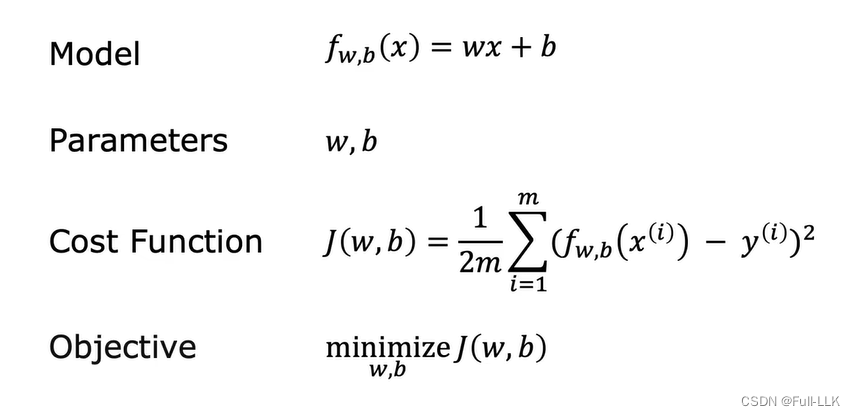
可视化即用图的形式表示
当损失函数取不同的参数值，损失函数的值可能不同可能相同
当以参数为平面，损失函数的值为纵轴，便可得到可视化的立体图
对应的平面时可将相同值的损失函数的值的平面点连接起来，这样就形成了等值线

梯度下降

作用：得到最小损失函数（不仅仅是线性回归）的值的参数取值
原理：每次微微改变参数使得尝试降低损失函数的值，最终使得其得到一个最小值

类似在损失函数可视化图中从某个位置跑到最低处

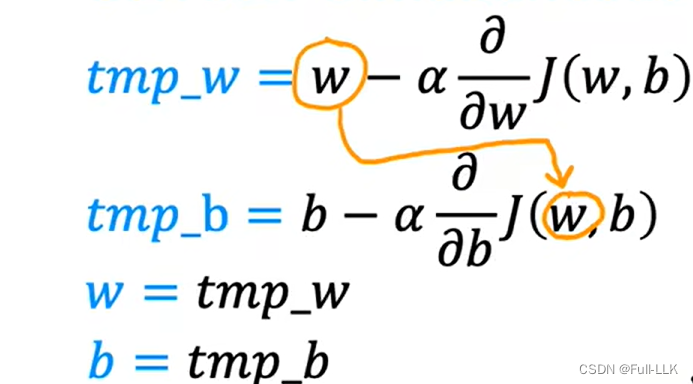
损失韩式对某个参数求导就是损失函数对某个参数的偏导数

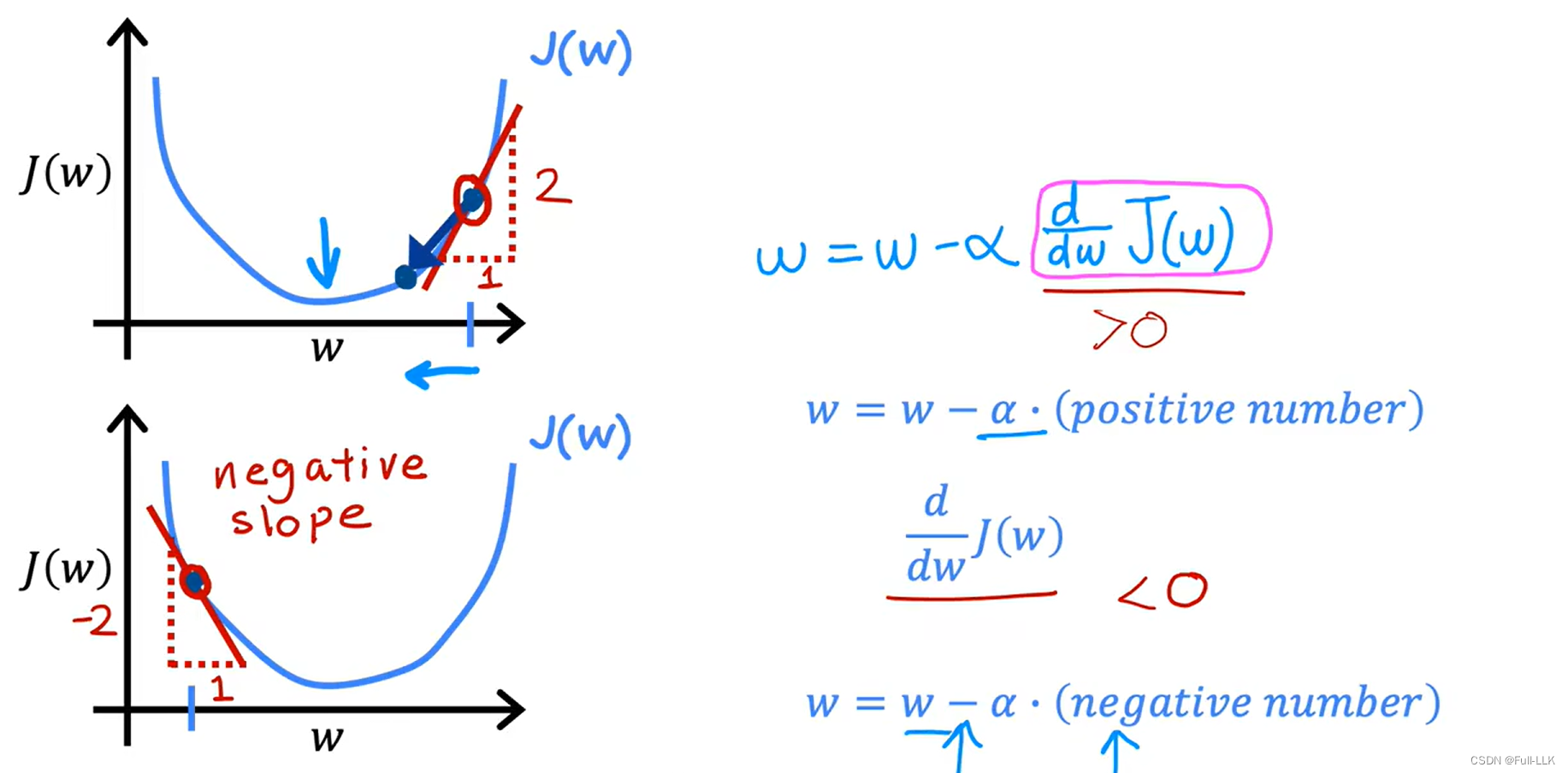
学习率：是一个固定的值

学习率如果过大，那么会导致w变化幅度过大，会在局部最小左右跳转，甚至离局部最小越来越远
学习率如果过小，那么会导致w变化幅度过小，要花很多步骤才会到达局部最小

偏导数会自动变化，当越接近局部最小时，对应的偏导数也会越小。此时学习率就算不变，但w的变化也会更小

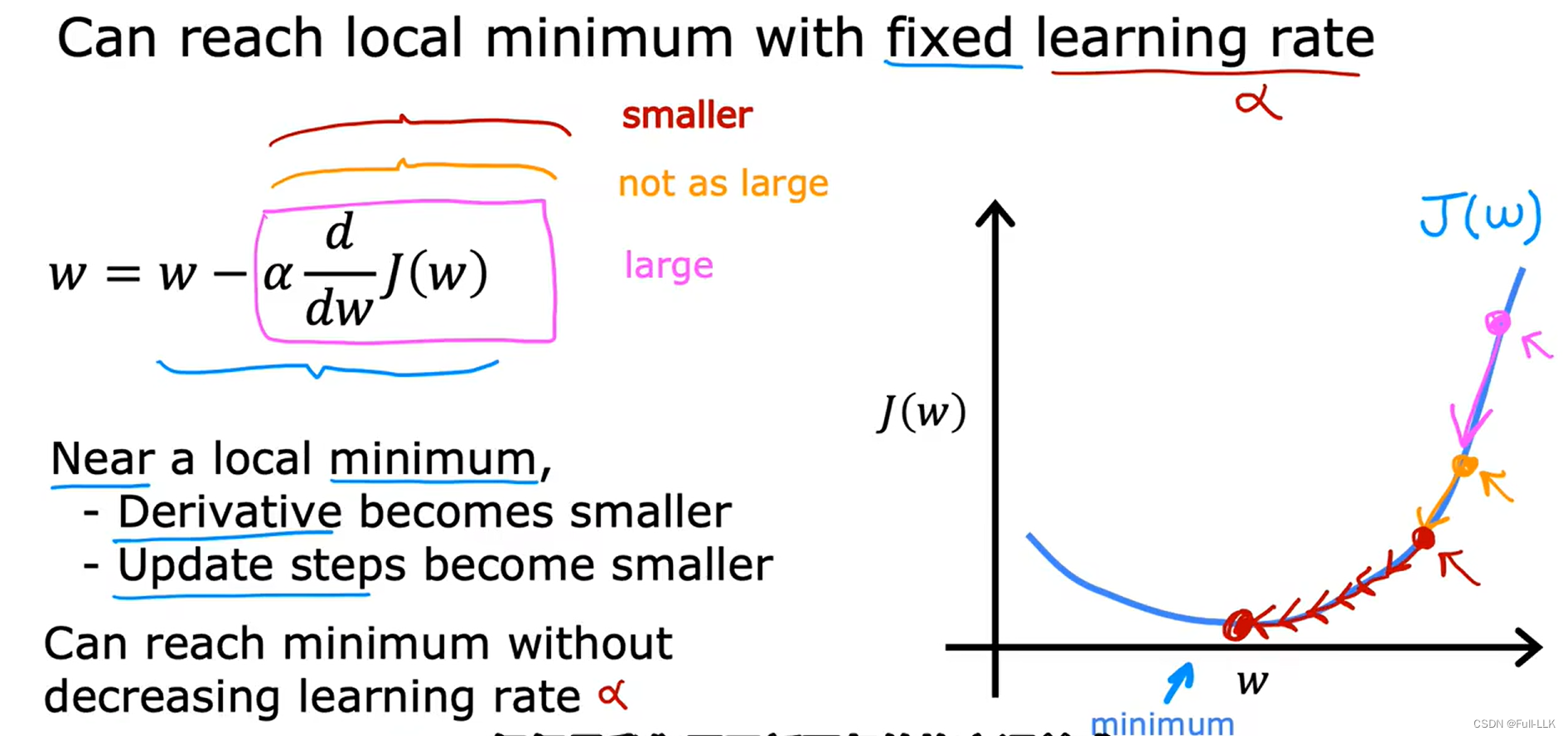
线性回归的平方误差损失函数

下图是递归下降的算法具体实现

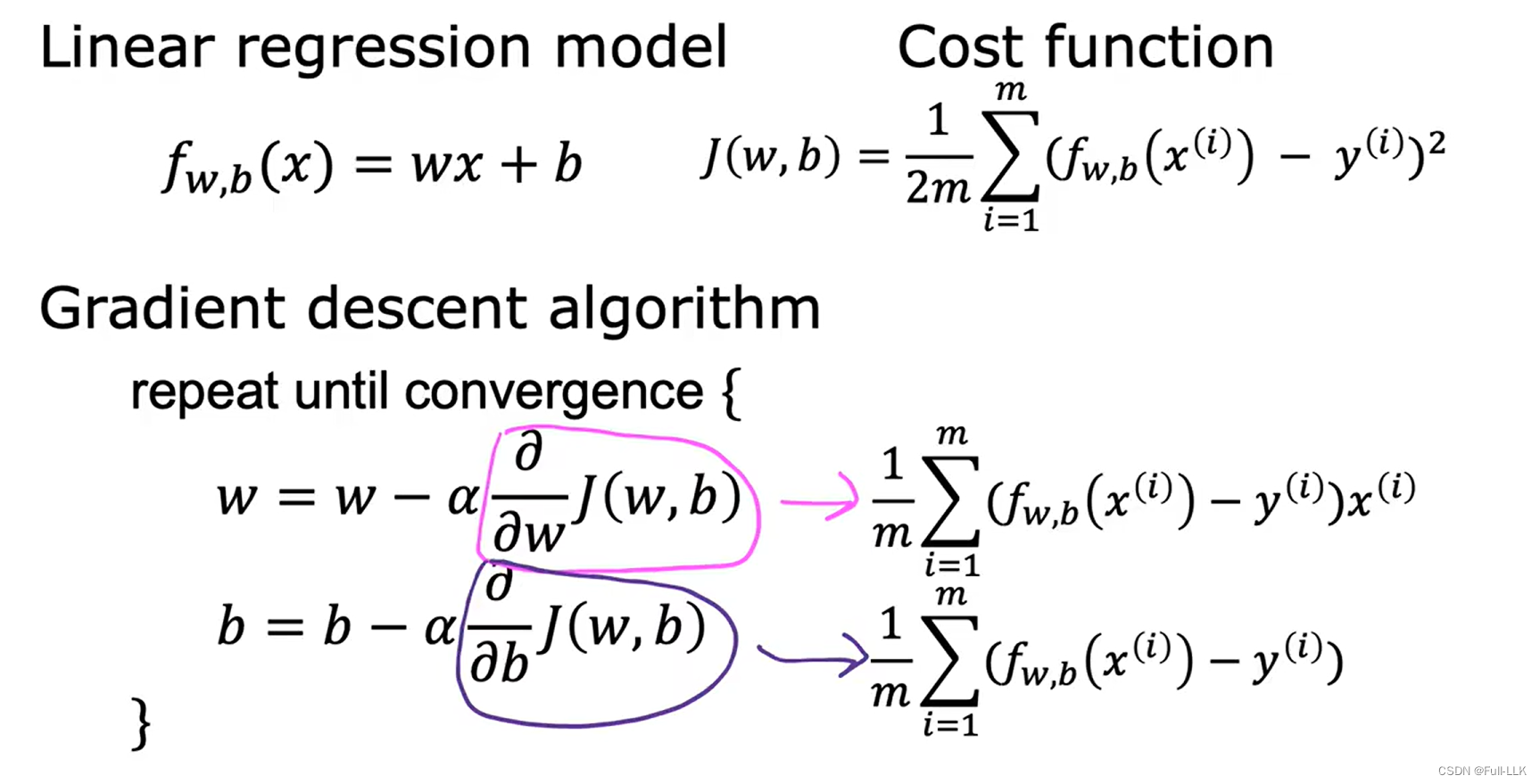
如下图如何得到相关偏导数

并且平方误差损失函数的可视化图是凹面图，即只有一个局部最小（即全局最小），而其他损失函数的可视化可能是类似丘陵，存在很多局部最小，从不同的参数位置开始递归下降可能得到不同的局部最小

lab实验

• scatter 函数来绘制散点图。

• plot 函数来根据点绘制直线

• legend()#在左上角显示相关图例代表的数据类型

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
from matplotlib.gridspec import GridSpec
from matplotlib.colors import LinearSegmentedColormap
from ipywidgets import interact
import copy
import mathplt.style.use('./deeplearning.mplstyle')
n_bin = 5dlblue = '#0096ff'; dlorange = '#FF9300'; dldarkred='#C00000'; dlmagenta='#FF40FF'; dlpurple='#7030A0'
dlc = dict(dlblue = '#0096ff', dlorange = '#FF9300', dldarkred='#C00000', dlmagenta='#FF40FF', dlpurple='#7030A0')
dlcolors = [dlblue, dlorange, dldarkred, dlmagenta, dlpurple]
dlcm = LinearSegmentedColormap.from_list('dl_map', dlcolors, N=n_bin)def compute_cost(X, y, w, b):m = X.shape[0]cost = 0.0for i in range(m):f_wb_i = np.dot(X[i],w) + b           #(n,)(n,)=scalarcost = cost + (f_wb_i - y[i])**2cost = cost/(2*m)return cost def plt_house_x(X, y,f_wb=None, ax=None):''' plot house with aXis '''if not ax:fig, ax = plt.subplots(1,1)ax.scatter(X, y, marker='x', c='r', label="Actual Value")ax.set_title("Housing Prices")ax.set_ylabel('Price (in 1000s of dollars)')ax.set_xlabel(f'Size (1000 sqft)')if f_wb is not None:ax.plot(X, f_wb,  c=dlblue, label="Our Prediction")ax.legend()def mk_cost_lines(x,y,w,b, ax):''' makes vertical cost lines'''cstr = "cost = (1/m)*("ctot = 0label = 'cost for point'addedbreak = Falsefor p in zip(x,y):f_wb_p = w*p[0]+bc_p = ((f_wb_p - p[1])**2)/2c_p_txt = c_pax.vlines(p[0], p[1],f_wb_p, lw=3, color=dlpurple, ls='dotted', label=label)label='' #just onecxy = [p[0], p[1] + (f_wb_p-p[1])/2]ax.annotate(f'{c_p_txt:0.0f}', xy=cxy, xycoords='data',color=dlpurple,xytext=(5, 0), textcoords='offset points')cstr += f"{c_p_txt:0.0f} +"if len(cstr) > 38 and addedbreak is False:cstr += "\n"addedbreak = Truectot += c_pctot = ctot/(len(x))cstr = cstr[:-1] + f") = {ctot:0.0f}"ax.text(0.15,0.02,cstr, transform=ax.transAxes, color=dlpurple)def plt_stationary(x_train, y_train):        # 绘制三个图，一个是某对w和b对应模型，一个是损失函数随着w和b变化的等值线图，一个是三维的损失函数随着w和b变化的变化# setup figure fig = plt.figure( figsize=(9,8))#fig = plt.figure(constrained_layout=True,  figsize=(12,10))fig.set_facecolor('#ffffff') #whitefig.canvas.toolbar_position = 'top'#gs = GridSpec(2, 2, figure=fig, wspace = 0.01)gs = GridSpec(2, 2, figure=fig)ax0 = fig.add_subplot(gs[0, 0])ax1 = fig.add_subplot(gs[0, 1])ax2 = fig.add_subplot(gs[1, :],  projection='3d')ax = np.array([ax0,ax1,ax2])#setup useful ranges and common linspacesw_range = np.array([200-300.,200+300])b_range = np.array([50-300., 50+300])b_space  = np.linspace(*b_range, 100)w_space  = np.linspace(*w_range, 100)# get cost for w,b ranges for contour and 3Dtmp_b,tmp_w = np.meshgrid(b_space,w_space)print(tmp_b)print(tmp_w)z=np.zeros_like(tmp_b)for i in range(tmp_w.shape[0]):for j in range(tmp_w.shape[1]):z[i,j] = compute_cost(x_train, y_train, tmp_w[i][j], tmp_b[i][j] )if z[i,j] == 0: z[i,j] = 1e-6w0=200;b=-100    #initial point### plot model w cost ###f_wb = np.dot(x_train,w0) + bmk_cost_lines(x_train,y_train,w0,b,ax[0])plt_house_x(x_train, y_train, f_wb=f_wb, ax=ax[0])### plot contour ###CS = ax[1].contour(tmp_w, tmp_b, np.log(z),levels=12, linewidths=2, alpha=0.7,colors=dlcolors)ax[1].set_title('Cost(w,b)')ax[1].set_xlabel('w', fontsize=10)ax[1].set_ylabel('b', fontsize=10)ax[1].set_xlim(w_range) ; ax[1].set_ylim(b_range)cscat  = ax[1].scatter(w0,b, s=100, color=dlblue, zorder= 10, label="cost with \ncurrent w,b")chline = ax[1].hlines(b, ax[1].get_xlim()[0],w0, lw=4, color=dlpurple, ls='dotted')cvline = ax[1].vlines(w0, ax[1].get_ylim()[0],b, lw=4, color=dlpurple, ls='dotted')ax[1].text(0.5,0.95,"Click to choose w,b",  bbox=dict(facecolor='white', ec = 'black'), fontsize = 10,transform=ax[1].transAxes, verticalalignment = 'center', horizontalalignment= 'center')#Surface plot of the cost function J(w,b)ax[2].plot_surface(tmp_w, tmp_b, z,  cmap = dlcm, alpha=0.3, antialiased=True)ax[2].plot_wireframe(tmp_w, tmp_b, z, color='k', alpha=0.1)plt.xlabel("$w$")plt.ylabel("$b$")ax[2].zaxis.set_rotate_label(False)ax[2].xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))ax[2].yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))ax[2].zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))ax[2].set_zlabel("J(w, b)\n\n", rotation=90)plt.title("Cost(w,b) \n [You can rotate this figure]", size=12)ax[2].view_init(30, -120)return fig,ax, [cscat, chline, cvline]#https://matplotlib.org/stable/users/event_handling.html
class plt_update_onclick:  # def __init__(self, fig, ax, x_train,y_train, dyn_items):self.fig = figself.ax = axself.x_train = x_trainself.y_train = y_trainself.dyn_items = dyn_itemsself.cid = fig.canvas.mpl_connect('button_press_event', self) # 鼠标点击时，会调用自己，即call函数def __call__(self, event):if event.inaxes == self.ax[1]:  # 点击发生的位置从而得到相应的w和bws = event.xdatabs = event.ydatacst = compute_cost(self.x_train, self.y_train, ws, bs)# clear and redraw line plotself.ax[0].clear()f_wb = np.dot(self.x_train,ws) + bs  mk_cost_lines(self.x_train,self.y_train,ws,bs,self.ax[0])  # 距离plt_house_x(self.x_train, self.y_train, f_wb=f_wb, ax=self.ax[0]) # 根据新的w和b得到模型函数# remove lines and re-add on countour plot and 3d plotfor artist in self.dyn_items:artist.remove()a = self.ax[1].scatter(ws,bs, s=100, color=dlblue, zorder= 10, label="cost with \ncurrent w,b")   b = self.ax[1].hlines(bs, self.ax[1].get_xlim()[0],ws, lw=4, color=dlpurple, ls='dotted')c = self.ax[1].vlines(ws, self.ax[1].get_ylim()[0],bs, lw=4, color=dlpurple, ls='dotted')d = self.ax[1].annotate(f"Cost: {cst:.0f}", xy= (ws, bs), xytext = (4,4), textcoords = 'offset points',bbox=dict(facecolor='white'), size = 10)            # 现在的#Add point in 3D surface plote = self.ax[2].scatter3D(ws, bs,cst , marker='X', s=100) # 3d图上画点self.dyn_items = [a,b,c,d,e]self.fig.canvas.draw()def inbounds(a,b,xlim,ylim): #判断w和b是否出界xlow,xhigh = xlimylow,yhigh = ylimax, ay = abx, by = bif (ax > xlow and ax < xhigh) and (bx > xlow and bx < xhigh) \and (ay > ylow and ay < yhigh) and (by > ylow and by < yhigh):return Truereturn Falsedef plt_contour_wgrad(x, y, hist, ax, w_range=[-100, 500, 5], b_range=[-500, 500, 5], # 等值线上迭代的w和b的变化contours = [0.1,50,1000,5000,10000,25000,50000],resolution=5, w_final=200, b_final=100,step=10 ):b0,w0 = np.meshgrid(np.arange(*b_range),np.arange(*w_range))z=np.zeros_like(b0)for i in range(w0.shape[0]):for j in range(w0.shape[1]):z[i][j] = compute_cost(x, y, w0[i][j], b0[i][j] ) CS = ax.contour(w0, b0, z, contours, linewidths=2,colors=[dlblue, dlorange, dldarkred, dlmagenta, dlpurple]) # 绘制等值线图ax.clabel(CS, inline=1, fmt='%1.0f', fontsize=10) # 等高线图上添加标签ax.set_xlabel("w");  ax.set_ylabel("b")ax.set_title('Contour plot of cost J(w,b), vs b,w with path of gradient descent')w = w_final; b=b_finalax.hlines(b, ax.get_xlim()[0],w, lw=2, color=dlpurple, ls='dotted')ax.vlines(w, ax.get_ylim()[0],b, lw=2, color=dlpurple, ls='dotted')base = hist[0]for point in hist[0::step]:edist = np.sqrt((base[0] - point[0])**2 + (base[1] - point[1])**2) # 计算当前点到到下一个w和b对应的坐标if(edist > resolution or point!=hist[-1]):  # 当跳转距离较大的时候或者还没到最后一个点的时候继续跳转if inbounds(point,base, ax.get_xlim(),ax.get_ylim()):plt.annotate('', xy=point, xytext=base,xycoords='data',arrowprops={'arrowstyle': '->', 'color': 'r', 'lw': 3},va='center', ha='center') # 在当前点绘制一个箭头base=pointreturndef plt_divergence(p_hist, J_hist, x_train,y_train):x=np.zeros(len(p_hist))y=np.zeros(len(p_hist))v=np.zeros(len(p_hist))for i in range(len(p_hist)):x[i] = p_hist[i][0]y[i] = p_hist[i][1]v[i] = J_hist[i]   # 对应的w和b和此时的损失函数值fig = plt.figure(figsize=(12,5))plt.subplots_adjust( wspace=0 )  # 子图间距的函数gs = fig.add_gridspec(1, 5)   # 5个空间放置子图，它们都将处于同一行内fig.suptitle(f"Cost escalates when learning rate is too large")#===============#  First subplot#===============ax = fig.add_subplot(gs[:2], )# Print w vs cost to see minimumfix_b = 100w_array = np.arange(-35000, 35000, 1000)cost = np.zeros_like(w_array)for i in range(len(w_array)):tmp_w = w_array[i]cost[i] = compute_cost(x_train, y_train, tmp_w, fix_b)ax.plot(w_array,cost)  # 损失函数随w的变化而变化ax.plot(x,v, c=dlmagenta) # 迭代过程中损失函数随着w的变化而变化ax.set_title("Cost vs w, b set to 100")ax.set_ylabel('Cost')ax.set_xlabel('w')ax.xaxis.set_major_locator(MaxNLocator(2))#===============# Second Subplot#===============tmp_b,tmp_w = np.meshgrid(np.arange(-35000, 35000, 5000),np.arange(-15000, 15000, 5000)) z=np.zeros_like(tmp_b) for i in range(tmp_w.shape[0]):for j in range(tmp_w.shape[1]):z[i][j] = compute_cost(x_train, y_train, tmp_w[i][j], tmp_b[i][j] )ax = fig.add_subplot(gs[2:], projection='3d') # 三维的损失函数随w和b的变化而变化ax.plot_surface(tmp_w, tmp_b, z,  alpha=0.3, color=dlblue) ax.xaxis.set_major_locator(MaxNLocator(2))ax.yaxis.set_major_locator(MaxNLocator(2))ax.set_xlabel('w', fontsize=16)ax.set_ylabel('b', fontsize=16)ax.set_zlabel('\ncost', fontsize=16)plt.title('Cost vs (b, w)')# Customize the view angleax.view_init(elev=20., azim=-65)ax.plot(x, y, v,c=dlmagenta) # 将迭代过程中的损失函数的值以及w和b的值return# draw derivative line
# y = m*(x - x1) + y1
def add_line(dj_dx, x1, y1, d, ax):   # 给损失函数上某个点画切线的x = np.linspace(x1-d, x1+d,50)y = dj_dx*(x - x1) + y1ax.scatter(x1, y1, color=dlblue, s=50) # 画点ax.plot(x, y, '--', c=dldarkred,zorder=10, linewidth = 1) # 画切线xoff = 30 if x1 == 200 else 10ax.annotate(r"$\frac{\partial J}{\partial w}$ =%d" % dj_dx, fontsize=14,  # 点旁边的注释xy=(x1, y1), xycoords='data',xytext=(xoff, 10), textcoords='offset points',arrowprops=dict(arrowstyle="->"),horizontalalignment='left', verticalalignment='top')def plt_gradients(x_train,y_train, f_compute_cost, f_compute_gradient):#===============#  First subplot#===============fig,ax = plt.subplots(1,2,figsize=(12,4))# Print w vs cost to see minimumfix_b = 100w_array = np.linspace(-100, 500, 50)w_array = np.linspace(0, 400, 50)cost = np.zeros_like(w_array)for i in range(len(w_array)):tmp_w = w_array[i]cost[i] = f_compute_cost(x_train, y_train, tmp_w, fix_b)ax[0].plot(w_array, cost,linewidth=1,label="cost function value")            # 画出损失函数图ax[0].set_title("Cost vs w, with gradient; b set to 100")ax[0].set_ylabel('Cost')ax[0].set_xlabel('w')# plot lines for fixed b=100for tmp_w in [100,200,300]:  # 画出损失函数上三个点的斜率fix_b = 100dj_dw,dj_db = f_compute_gradient(x_train, y_train, tmp_w, fix_b )j = f_compute_cost(x_train, y_train, tmp_w, fix_b)add_line(dj_dw, tmp_w, j, 30, ax[0])#===============# Second Subplot#===============tmp_b,tmp_w = np.meshgrid(np.linspace(-200, 200, 10), np.linspace(-100, 600, 10))U = np.zeros_like(tmp_w)V = np.zeros_like(tmp_b)for i in range(tmp_w.shape[0]):for j in range(tmp_w.shape[1]):U[i][j], V[i][j] = f_compute_gradient(x_train, y_train, tmp_w[i][j], tmp_b[i][j] ) # 计算一系列损失函数上关于w的斜率X = tmp_wY = tmp_bn=-2color_array = np.sqrt(((V-n)/2)**2 + ((U-n)/2)**2)print(V)ax[1].set_title('Gradient shown in quiver plot')Q = ax[1].quiver(X, Y, U, V, color_array, units='width') # 根据斜率确定箭头的方向ax[1].quiverkey(Q, 0.9, 0.9, 2, r'$2 \frac{m}{s}$', labelpos='E',coordinates='figure') # 在右上角增加一个图例ax[1].set_xlabel("w"); ax[1].set_ylabel("b")def compute_gradient(x, y, w, b):   # 计算w和b此时对应的偏导数（梯度）# Number of training examplesm = x.shape[0]    dj_dw = 0dj_db = 0for i in range(m):  f_wb = w * x[i] + b dj_dw_i = (f_wb - y[i]) * x[i] dj_db_i = f_wb - y[i] dj_db += dj_db_idj_dw += dj_dw_i dj_dw = dj_dw / m dj_db = dj_db / m return dj_dw, dj_dbdef gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function):  # 从起始位置迭代规定次数，最后得到合适的参数w = copy.deepcopy(w_in) # avoid modifying global w_in# An array to store cost J and w's at each iteration primarily for graphing laterJ_history = []p_history = []b = b_inw = w_infor i in range(num_iters):# Calculate the gradient and update the parameters using gradient_functiondj_dw, dj_db = gradient_function(x, y, w , b)     # Update Parameters using equation (3) aboveb = b - alpha * dj_db                            w = w - alpha * dj_dw                            # Save cost J at each iterationif i<100000:      # prevent resource exhaustion J_history.append( cost_function(x, y, w , b))p_history.append([w,b])# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters/10) == 0:print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e}  ",f"w: {w: 0.3e}, b:{b: 0.5e}")return w, b, J_history, p_history #return w and J,w history for graphingx_train=np.array([1.0,2.0])
y_train=np.array([300.0,500.0])    # 训练数据初始化
"""
fig, ax, dyn_items = plt_stationary(x_train, y_train)
updater = plt_update_onclick(fig, ax, x_train, y_train, dyn_items)
plt.show()                 # 动态变化w和b对应的模型和其与训练数据的差plt_gradients(x_train,y_train, compute_cost, compute_gradient)
plt.show()             # 得到损失函数随w的变化而变化的趋势w_final,b_final,J_hist,p_hist=gradient_descent(x_train,y_train,10,20,0.01,10000,compute_cost,compute_gradient)# 通过梯度下降得到合适的w和b值fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4)) # 绘制梯度下降过程中损失函数随迭代次数的变化的变化
ax1.plot(J_hist[:100]) # 前100次
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:]) # 所有的次数
ax1.set_title("Cost vs. iteration(start)");  ax2.set_title("Cost vs. iteration (end)")
ax1.set_ylabel('Cost')            ;  ax2.set_ylabel('Cost') 
ax1.set_xlabel('iteration step')  ;  ax2.set_xlabel('iteration step') 
plt.show()print(f"1000 sqft house prediction {w_final*1.0 + b_final:0.1f} Thousand dollars")  # 利用得到的模型预测结果
print(f"1200 sqft house prediction {w_final*1.2 + b_final:0.1f} Thousand dollars")
print(f"2000 sqft house prediction {w_final*2.0 + b_final:0.1f} Thousand dollars")fig, ax = plt.subplots(1,1, figsize=(12, 6))
plt_contour_wgrad(x_train, y_train, p_hist, ax) # 在等值线中绘制梯度下降过程中w和b随迭代次数的变化的变化
plt.show()w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, 100, 100, 0.8, 10, compute_cost, compute_gradient)
plt_divergence(p_hist, J_hist,x_train, y_train) # 观察当学习率较大时候在损失函数上w和b的位置的变化
plt.show()"""