参考资料:python统计分析【托马斯】
1、单样本均值的t检验
检验一个正态分布数据的均值和一个参考值的差异,我们一般使用单样本t检验,该检验基于t分布。
如果我们知道一个正态分布总体的均值和标准差,那么我们可以计算对应的标准误,并用来自正态分布的值来判断得到一个特定值的可能性大小。然而,在实际中,我们必须从样本中估计均值和标准差;并且用来描述来自正态分布的样本均值的t分布。
我们从均值为7、标准差为3的正态分布中抽取100个数据。
# 导入库
import numpy as np
from scipy import stats
import random# 设置正态分布
normal=stats.norm(7,3)
# 设置随机种子,用于复现结果
random.seed(1234)
# 从正态分布中抽取100个数据
sample=normal.rvs(100)# 输出样本均值和标准差
print("样本均值:",sample.mean())
print("样本标准差:",sample.std(ddof=1))
检验样本均值6.83是否与总体均值7是否有显著差异,使用如下函数:
t,pVal=stats.ttest_1sample(data,checkVale)
t,pVal=stats.ttest_1samp(sample,7)
print("t统计量:",t)
print("p值",pVal)
结论:p值大于0.05,样本均值与总体均值差异不显著。
可参考:python统计分析——单样本t检验_单样本t分布检验python代码-CSDN博客
2、单样本均值的Wilcoxon符号秩和检验
在非正态分布的数据中,我们不应该使用单样本t检验。相反我们必须使用均值的非参数检验方法。我们可以进行Wilcoxon符号秩和检验。
wil,pVal=stats.wilcoxon(data-checkValue)
该方法有3个步骤:
①计算每个观测值和感兴趣的值的差异;
②忽略差异的符号,将它们按照大小排序;
③将所有负(或正)秩次的秩次加起来,也就是哪些低于(或高于)选定的假设值的秩次。
案例参考:

# 输入案例数据
sample=np.array([5260,5470,5640,6180,6380,6515,6805,7515,7515,8230,8770])
# 进行Wilcoxon秩和检验
wil,pVal=stats.wilcoxon(sample-7515)
print("统计量:",wil)
print("p值:",pVal)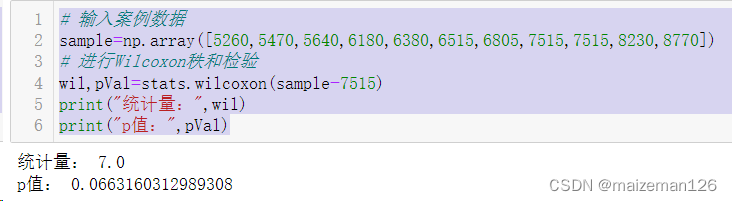
结论:样本的中位数与7515差异不显著。







和IP范围段(IP/24))











