669. 修剪二叉搜索树
669. 修剪二叉搜索树 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
你修剪的方式不对,我来给你纠正一下!| LeetCode:669. 修剪二叉搜索树_哔哩哔哩_bilibili
给你二叉搜索树的根节点
root,同时给定最小边界low和最大边界high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
输入:root = [1,0,2], low = 1, high = 2 输出:[1,null,2]示例 2:
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出:[3,2,null,1]提示:
- 树中节点数在范围
[1, 104]内0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
刚开始想得很简单,就是把左节点和区间的最小值比较,右节点和区间最大值比较,也算利用了二叉搜索树的特点,但是后来反应过来不能这样粗暴地一分为二,因为左节点连接的右子树上可能有在区间内的值,右节点连接的左子树可能有在区间内的值。
看卡哥视频题解:
递归三部曲:
1、确定参数和返回值:参数是传入的根节点root和区间。最终删除节点完成后返回根节点,就是符合区间的二叉树:
public TreeNode trimBST(TreeNode root, int low, int hight){}2、确定终止条件:遇到空姐点就返回,不然就会无休止地遍历:
if(root == null){return null;
}3、确定单层递归的逻辑:如果根节点的值小于区间的左边界的值,则递归右子树,返回右子树符合条件的头节点;如果根节点的值大于区间的右边界的值,则递归左子树,返回左子树符合条件的头节点。然后根节点更新它的左右节点,把新的递归上来的节点接住,形成新的裁剪后的二叉树:
if(root.val < low){return trimBST(root.right, low, hight);
}
if(root.val > low){return trimBST(root.left, low, hight);
}
root.left = trimBST(root.left, low, hight);
root.right = trimBST(root.right, low, hight);
return root;综合代码:
class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if (root == null) {return null;}if (root.val < low) {return trimBST(root.right, low, high);}if (root.val > high) {return trimBST(root.left, low, high);}// root在[low,high]范围内root.left = trimBST(root.left, low, high);root.right = trimBST(root.right, low, high);return root;}
}
108.将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
构造平衡二叉搜索树!| LeetCode:108.将有序数组转换为二叉搜索树_哔哩哔哩_bilibili
给你一个整数数组
nums,其中元素已经按 升序 排列,请你将其转换为一棵平衡 二叉搜索树。
示例 1:
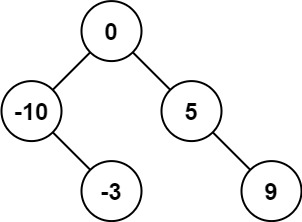
输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
第一反应是求数组的中位数,如果是奇数个节点,就求中位数;如果是偶数(n)个节点,就求第(n+1)/2位置的数为中位数,中位数为根节点,左区间的中位数为左节点,右区间的中位数为右节点,不断递归得最终的平衡二叉搜索树。
看了卡哥题解,思路Bingo!!!
递归三部曲:
1、确定参数和返回值:参数是数组和左右下标,返回值就是把根节点原地返回:
private TreeNode traversal(int[] nums, int left, int right){}2、确定终止条件:我在划分区间的时候选择的是左闭右闭区间,所以终止条件就是left>right,这时候数组里面的数就遍历完了:
if(left > right){return null;
}3、确定单层递归的逻辑:首先计算中间节点,该节点为根节点;然后构建左右子树,最后返回根节点:
int mid = left + ((right - left) >> 1); // 计算当前区间的中间索引,采用位运算右移1位相当于除以2,避免溢出。
TreeNode root = new TreeNode(nums[mid]); // 创建一个树节点,值为当前区间的中间值。
root.left = traversal(nums, left, mid - 1); // 递归构建左子树,区间为[left, mid - 1]。
root.right = traversal(nums, mid + 1, right); // 递归构建右子树,区间为[mid + 1, right]。
return root; // 返回当前根节点。综合代码:
class Solution { // 定义一个名为Solution的类public TreeNode sortedArrayToBST(int[] nums) { // 定义一个名为sortedArrayToBST的公共方法,接受一个整型数组作为输入,并返回一个TreeNode类型的根节点。这个方法的作用是将给定的有序数组转换为平衡二叉搜索树。TreeNode root = traversal(nums, 0, nums.length - 1); // 调用traversal方法,传入nums数组、数组的起始索引0和结束索引nums.length - 1,并将返回的根节点赋值给root。return root; // 返回根节点root。}// 左闭右闭区间[left, right]private TreeNode traversal(int[] nums, int left, int right) { // 定义一个名为traversal的私有方法,接受一个整型数组nums和两个整数left和right作为参数。该方法用于递归构建二叉搜索树。if (left > right) return null; // 如果left大于right,说明当前区间为空,直接返回null。int mid = left + ((right - left) >> 1); // 计算当前区间的中间索引,采用位运算右移1位相当于除以2,避免溢出。TreeNode root = new TreeNode(nums[mid]); // 创建一个树节点,值为当前区间的中间值。root.left = traversal(nums, left, mid - 1); // 递归构建左子树,区间为[left, mid - 1]。root.right = traversal(nums, mid + 1, right); // 递归构建右子树,区间为[mid + 1, right]。return root; // 返回当前根节点。}
}
538.把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
普大喜奔!二叉树章节已全部更完啦!| LeetCode:538.把二叉搜索树转换为累加树_哔哩哔哩_bilibili
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点
node的新值等于原树中大于或等于node.val的值之和。提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: . - 力扣(LeetCode) 相同
示例 1:
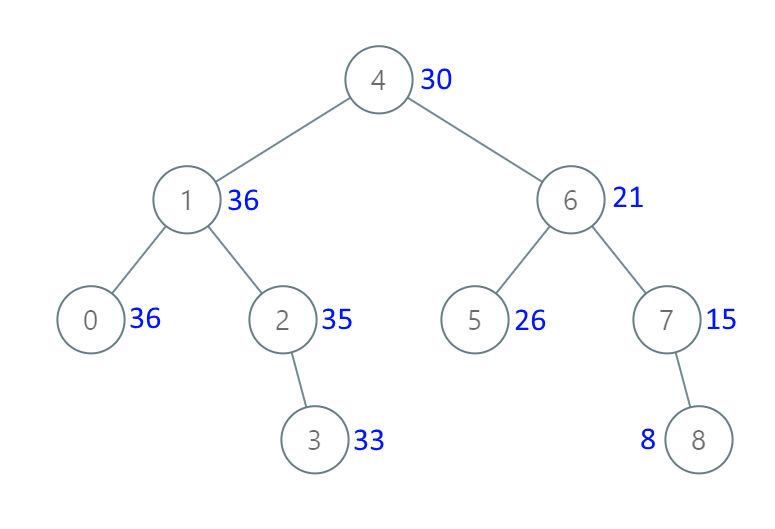
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]示例 2:
输入:root = [0,null,1] 输出:[1,null,1]示例 3:
输入:root = [1,0,2] 输出:[3,3,2]示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]提示:
- 树中的节点数介于
0和104之间。- 每个节点的值介于
-104和104之间。- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
题目没读懂,主要是累加树不懂,直接看卡哥题解了:
理解了累加树是什么之后还挺简单的,但是没想到双指针法。遍历方式为右中左:
递归三部曲:
1、确定参数和返回值:是根节点root:
public void convertBST1(TreeNode root){}2、确定终止条件:遇到空节点就终止:
if (root == null) {return;
}3、确定单层递归的逻辑:右中左来遍历二叉树, 中节点的处理逻辑就是让cur的数值加上前一个节点的数值。
convertBST1(root.right);
sum += root.val;
root.val = sum;
convertBST1(root.left);综合代码:
class Solution {int sum; // 声明一个整数变量 'sum' 用于存储节点值的累加和。// 将给定的二叉搜索树转换为累加和树的方法public TreeNode convertBST(TreeNode root) {sum = 0; // 在调用辅助函数之前将sum初始化为0。convertBST1(root); // 调用辅助函数执行转换。return root; // 返回修改后的树的根节点。}// 辅助函数通过右根左的顺序遍历树执行转换public void convertBST1(TreeNode root) {if (root == null) { // 如果当前节点为null,则返回。return;}convertBST1(root.right); // 递归地在右子树上调用函数。sum += root.val; // 将当前节点的值添加到累加和中。root.val = sum; // 将当前节点的值更新为累加和。convertBST1(root.left); // 递归地在左子树上调用函数。}
}
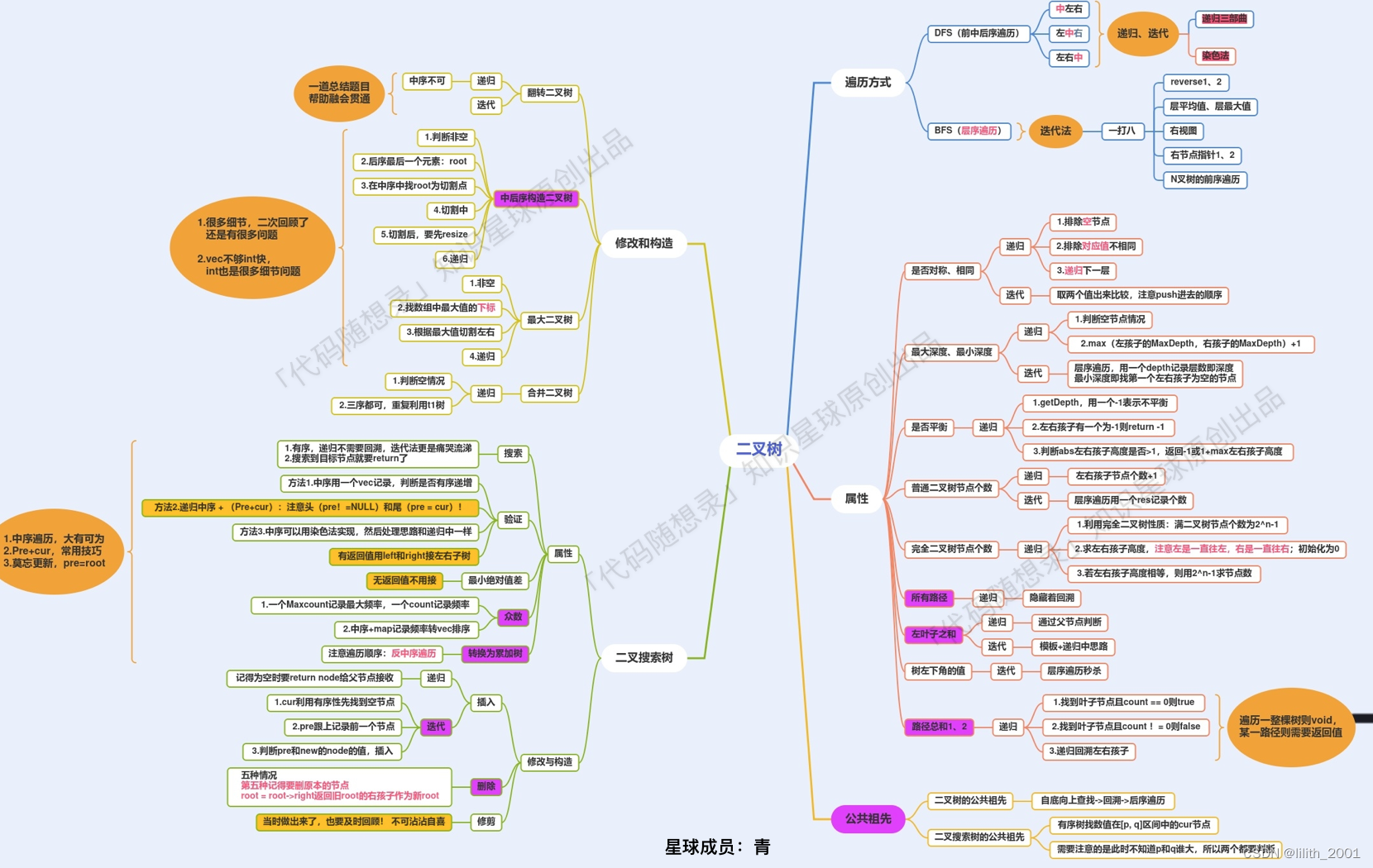
二叉树总结:












)
)





)



![[Linux]条件变量:实现线程同步(什么是条件变量、为什么需要条件变量,怎么使用条件变量(接口)、例子,代码演示(生产者消费者模型))](http://pic.xiahunao.cn/[Linux]条件变量:实现线程同步(什么是条件变量、为什么需要条件变量,怎么使用条件变量(接口)、例子,代码演示(生产者消费者模型)))