在这篇文章之前，笔者只是简单了解过位运算相关概念，但是每次刷LeetCode碰到位运算相关题目，都会敬而远之。一方面是觉得看起来晦涩难懂，另一方面觉得日常开发用处不大。

        近期本着学习的目的，静下心来研究了一下，感觉位运算确实巧妙，而且涉及知识点还不少，这里来总结一下初步接触位运算的收获。本文是基于JavaScript来进行讲解。

---

什么是位运算

        所谓位运算，就是对二进制位进行操作的运算方式。

        例如我们需要对「15」这个10进制整数进行位运算。位运算符首先会将15转换成32位的二进制串，然后再对二进制进行运算。运算后得出结果，会再次转换成标准的十进制数字，然后返回。

   例:     15 => '0000 0000 0000 0000 0000 0000 0000 1111'

首先，这里有几个知识点需要记住：

        1、位运算会将数值会转成32位的二进制。对任何数进行位运算都会转换成一个固定长度为32位的由0和1组成的二进制串。如果有一个整数很大，转换成二进制之后，位数超过32位了，那么超出的部分将会被丢弃，这样在做位运算的时候结果肯定是不准确的。因此在使用位运算的时候，确保要处理的数值转换成二进制之后不会超过32位的范围。安全范围也就是[-2147483648, 2147483647]，也可以说(-2)^31 至 (2^31) -1。

        2、第一位是符号位。在JavaScript中，位运算的32位二进制是包括符号位的。第一位通常被用作符号位，用来确定数据的正负，0表示正数，1表示负数。

        3、负数用补码表示。计算机内部是用补码来表示负数的。简单来说补码就是原码取反后+1。二进制原码补码相关规则忘记的小伙伴自行百度，这里不再详细介绍。

示例： -1 的二进制是什么呢。

首先-1用原码表示为”10000000 00000000 00000000 00000001“

然后按位取反（除符号位）："11111111 11111111 11111111 11111110"

最后再加1。

因此-1用二进制表示为：”11111111 11111111 11111111 11111111“

        至于位运算为什么必须是32位，只能说是出于规范的一致性，以及简化底层数据处理。

扩展知识点：

        1、在js中，将一个正整数转换成二进制可以通过toString方法

let a = 15;
a.toString(2);    // '1111'

        2、js中并没有直接返回一个负数二进制的方法，如果想要返回一个负数的二进制，则需要根据补码的规则编写一个简单函数来返回。

常见的位运算

        常见的位运算包括：按位与（AND）、按位或（OR）、按位异或（XOR）、按位取反（NOT）、左移（Shift Left）和右移（Shift Right）

        1、按位与（ & ）：两个二进制位都为1时，结果才为1。

        2、按位或（ | ）：两个二进制位只要有一个为1，结果就为1。

        3、按位异或（ ^ ）：两个二进制位必须一个为1，一个为0，结果才为1。（ 任何数跟0异或都是本身，跟本身异或都为0）

        4、按位取反（ ~ ）：如果一个二进制位为1，结果为0；如果为0，结果为1。

        5、左移（ << ）：将二进制整体向左移动。右侧用0填充

        6、有符号右移（ >> ）：将二进制整体向右移动，左侧用符号位填充(符号位是0填充0，符号位是1填充1)。

        7、无符号右移（ >>> ）：将二进制整体向右移动(符号位看做普通二进制位),左侧用0填充。

实战讲解

        掌握了上面这些基础的概念之后，我们来做几道算法题。

题目1：LeetCode上第136题《只出现一次的数字》

        给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

        你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

示例 1 ：

        输入：nums = [2,2,1]
        输出：1
示例 2 ：

        输入：nums = [4,1,2,1,2]
        输出：4
示例 3 ：

        输入：nums = [1]
        输出：1

提示：

        1 <= nums.length <= 3 * 10^4
        -3 * 10^4 <= nums[i] <= 3 * 10^4
        除了某个元素只出现一次以外，其余每个元素均出现两次。

思路分析：

        如果没有空间复杂度限制的话，我们可以定义一个set。只需遍历一遍数组。判断set是否存在，不存在则添加；存在则删除。最终set中剩下的肯定是只出现一次的数字。

        但是题目要求我们只能用常量额外空间来处理。同时根据提示中的范围，我们知道数组中的整数，没超过位运算的安全范围，所以我们可以考虑使用位运算来做。

        考虑到位运算，我们根据上文中异或运算的特性——任何数和0异或等于本身，和本身异或等于0。因此如果我们对数组中的每个数都进行一次异或。重复的肯定消失，最后剩下的则是那唯一的值。

        代码如下：

var singleNumber = function (nums) {let result = 0;for (const item of nums) {result = result ^ item;}return result;
};

题目2：LeetCode上第137题《只出现一次的数字 II》

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

示例 1：

        输入：nums = [2,2,3,2]
        输出：3
示例 2：

        输入：nums = [0,1,0,1,0,1,99]
        输出：99

提示：

        1 <= nums.length <= 3 * 10^4
        -2^31 <= nums[i] <= 2^31 - 1
        nums 中，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次

思路分析：

        跟第一题同理，如果没有空间复杂度限制的话，这题目也比较简单。首先遍历一遍数组，定义一个map记录一下出现次数，然后再遍历一遍，输出次数为1的元素即可。

        根据提示给出的范围，正好满足位运算的安全范围。不过这题相对第一题来说复杂一点，我们来提供一种思路。

        首先根据位运算的规则我们知道，在进行位运算的时候，会将整数转换成2进制后进行运算，因此我们将示例1的输入值 [ 2,2,3,2 ] 转换成二进制如下所示。 

        根据上图我们能够发现，最后一列有1个1，倒数第2列有4个1。

        假如有一个数出现了3次，那么在相对应的2进制位上，肯定也会出现3次。

        接着我们统计一下每一个二进制位1的个数，然后跟3取余，最后结果就是要找的那个数。

        如上图所示，每一位和3取余之后，结果为 "0011" 。而"0011"的二进制则为3。

        有了这个思路之后我们接下来要做的就是想办法统计每一个二进制位上1的个数。首先如何判断一个二进制位是1还是0呢，根据位运算中按位与的概念，「1 & 1 === 1」，「1 & 0 === 0」

        我们拿一个代表性的数字10举例，10 的二进制是"1010"。10 & 1结果是什么呢？

        如图所示，结果是0。然后我们让10右移一位（右移一位的结果我们这里并不需要关注），再跟1做与运算

        如图所示，结果是1。我们发现一个数跟1进行与运算，能判断出最后一位是否是1。然后每次都让数字右移一位，就能判断出每一位是否是1。

        知道这些之后我们回归题目来整体梳理一下逻辑。我们让数组中每一个数都跟1进行与运算，如果为1则累加。最后能够得到最后一列中有几个1。然后我们让每个数都右移一位，重新计算，以此类推就能够得到每一个位置有几个1。我们还知道二进制位有32位，所以我们只需要移动31次即可。代码如下

var singleNumber = function (nums) {for (let i = 0; i < 32; i++) {let sum = 0;for (const item of nums) {sum += (item >> i) & 1;}console.log('倒数第i列1的个数为：', sum);}};

        核心代码是第六行，我们将每个数移动i位，然后跟1进行与运算并累加。就得到能从后往前第i列有几个1。

        到这里还没结束呢，我们还需要将每一位跟3取余，并得到最终结果。

        这里想先问一下大家日常根据一个二进制怎么计算10进制呢。相信很多人跟笔者一样都是使用一二四八大法吧。随便定义一个二进制，"1010101" 结果是什么呢？

        从后往前第一位是1，第二位是2，第三位是4，第四位是8，前一位是后一位的两倍。能够得到下图。

        然后我们用1+4+16+64，能得到答案—— 85。

        之后我们再假设一下让数字1左移的话会有什么效果。能发现左移1位变为2，左移2位变为4，左移3位变为8。

        知道这个之后，我们来看完整代码

var singleNumber = function (nums) {let res = 0;for (let i = 0; i < 32; i++) {let sum = 0;for (const item of nums) {sum += (item >> i) & 1;}if (sum % 3 !== 0) {res += (1 << i);}}return res;
};

        这段代码只需关注11-13行。当我们统计到1的个数之后跟3取余，如果不等于0，说明这个二进制位就是要找的数据的某一个二进制位，然后让1左移i位，累加起来。最后的结果就是结果数据。

题目3：LeetCode上第260题《只出现一次的数字 III》

给你一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。

示例 1：

        输入：nums = [1,2,1,3,2,5]
        输出：[3,5]
        解释：[5, 3] 也是有效的答案。
示例 2：

        输入：nums = [-1,0]
        输出：[-1,0]
示例 3：

        输入：nums = [0,1]
        输出：[1,0]

提示：

        2 <= nums.length <= 3 * 10^4
        -2^31 <= nums[i] <= 2^31 - 1
        除两个只出现一次的整数外，nums 中的其他数字都出现两次

     这道题是在第一题的基础上，增加了一个只出现一次的元素。因此我们无法直接通过异或得到结果。因为异或后的最终结果是那两个数异或后的值。

        所以我们需要考虑的是有没有办法将这两个异或后的值拆分出来，是解题关键。

        这道题解法太巧妙了，笔者想破脑袋也想不到啊，仅针对LeetCode官方给出的解法，给大家解释明白。

        首先我们根据异或的概念知道，两个数不一样，结果才为1。这里我们假设最终结果A和B。如果A^B的结果二进制中有一位是1，那么肯定要不就是A中的，要不就是B中的，

        我们如果将一个数转换成2进制，并且需要找出其中一个二进制位是1的位置，相信大家有很多办法。官方给出找这个位置的巧妙办法是这样的。

        假设最终求出的两个结果为A和B。将A和B的异或结果（A ^ B）设为X。那么X 和负X进行与运算(x & -x)得出的结果，就是X中最低位的那个1。举几个例子：

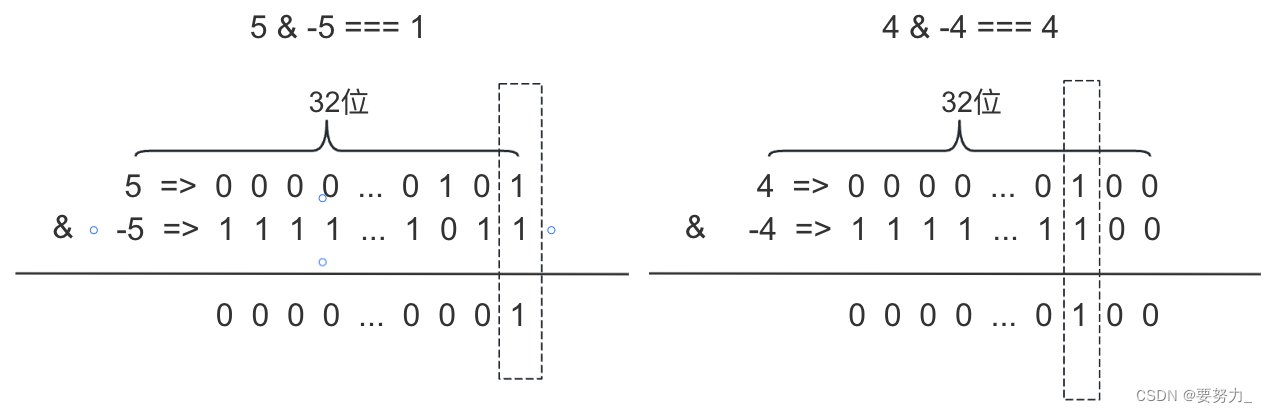
       （妙，妙到家了，这谁能想到啊。当然，我们也可以用其他办法随便找个二进制位为1的位置。剩下的处理逻辑是一样的）

        得到这个数之后，我们拿每个数都跟这个结果进行与运算。结果只有两种情况，要不就是1，要不就是0。上面讲过了，这个数非A即B，如果这个数是跟A与运算结果是1，那么B肯定是0。反之也一样。这样我们就可以将所有的数分为两部分，其中A和B肯定没有在一起。

        至于其他数，相同的数肯定在同一部分，再对这两部分分别进行异或运算，则两部分就只会剩下A和B了。代码如下：

var singleNumber = function(nums) {let answer = 0;// 首先对数组中所有数进行异或运算，得到结果A和结果B的异或结果 answerfor(const item of nums) {answer ^= item;}// 然后通过异或结果跟相反数进行与运算，得到一个表示异或结果最低位为1的值const index =  answer & (-answer);let left = 0;let right = 0;for(const item of nums) {// 遍历每一个数，跟index与运算为1的放左边，为0的放右边if (item & index) {//  对左边的所有数进行异或运算left ^= item;} else {//  对右边的所有数进行异或运算right ^= item;}}// 最终left只剩下一个，right也只剩下一个，为最后答案return [left, right]
};