目录

CM11链表分割

 OR36 链表的回文结构

 160.相交链表

 141&142环形链表

CM11链表分割

step1:思路分析 

1.首先可以想到，我们可以将原链表的元素划分到两个新的链表之中，由于必须保持顺序，所以新链表我们要用尾插。

2.为了方便进行尾插我们可以选择定义两个新的头结点。

step2:书写代码

class Partition {
public:ListNode* partition(ListNode* pHead, int x) {struct ListNode *LessPhead,*LessTail,*GreaterPhead,*GreadtTail;LessTail=LessPhead=( struct ListNode*) malloc(sizeof(struct ListNode));GreadtTail=GreaterPhead=( struct ListNode*) malloc(sizeof(struct ListNode));LessTail->next=GreadtTail->next= NULL;ListNode*cur=pHead;while(cur){if(cur->val<x){ListNode*pre1=cur;LessTail->next=pre1;LessTail=pre1;}else{   ListNode*pre2=cur;GreadtTail->next=pre2;GreadtTail=pre2;}cur=cur->next;}LessTail->next=GreaterPhead->next;GreadtTail->next= NULL;pHead=LessPhead->next;free(LessPhead);free(GreaterPhead);return  pHead;}
};

 OR36 链表的回文结构

step1：分析思路 

1.首先可以看到我们空间复杂度是有O（1）的要求的，所以不能开辟数组暴力解决。

2.我们想到回文结构是对称的，首先想到肯定是如何找到中间节点，之前写过求中间结点的代码，这次可以直接引用。

3.找到中间节点后，我们们可以让后续的翻转一下位置，又可以借用翻转链表的代码。

4.然后就是定义头和中间节点，遍历比对，实现判断。

step2：代码书写

struct ListNode {int val;struct ListNode *next;ListNode(int x) : val(x), next(NULL) {}};#include <exception>
struct ListNode* middleNode(struct ListNode* head) {struct ListNode* cur1=head;struct ListNode* cur2=head;int count=0;int i=1;while(cur1->next){cur1=cur1->next;count++;}count++;while(i!=count/2+1){cur2=cur2->next;i++;}    return cur2;}
struct ListNode* reverseList(struct ListNode* head){//我的想法：第一种 建立一个新的链表头插struct ListNode* cur=head;struct ListNode* tail=NULL;while(cur){struct ListNode* next=cur->next; cur->next=tail;tail=cur;cur=next;}return tail;}
class PalindromeList {
public:bool chkPalindrome(ListNode* A) {struct ListNode*mid= middleNode(A);struct ListNode*rehead=reverseList(mid);while(A&&rehead){if(A->val!=rehead->val){return false;}rehead=rehead->next;A=A->next;}return true;}
};

 160.相交链表

 

step1：分析思路

我们很容易想到由于单链表的特性 不可能存在next指针指向两个位置，因此只能是二合一并且尾部是保持单链的情况。

1.尝试反向遍历，违反单链表特性。

2.用一个数组存储一个链表的元素然后和另一个链表元素进行比较，显然时间复杂度因该是

O（N）空间复杂度也变成了O（N）。可行

3.统计链表长度，然后计算长度差值，长表先走相应的差值使得两个指针能够同步走，对比第一次元素相等时，就是想要的结果。时复O（N）  空复O(1)

step2：代码书写

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {struct ListNode* cur1=headA;struct ListNode* cur2=headB;int count1=0;int count2=0;while(cur1->next){cur1=cur1->next;count1++;}count1++;while(cur2->next){cur2=cur2->next;count2++;}count2++;if(cur1!=cur2)//勿忽略{return NULL;}int gap=abs(count1-count2);struct ListNode*longlist=headA;struct ListNode*shortlist=headB;if(count1<count2){longlist=headB;shortlist=headA;}while(gap--){longlist=longlist->next;}while(longlist!=shortlist){longlist=longlist->next;shortlist=shortlist->next;}return shortlist;}

注意1：int gap=abs(count1-count2); //这是取了一个绝对值。

注意2：if(cur1!=cur2)//勿忽略
           {
                  return NULL;
            }
 

 141&142环形链表

step1：分析思路

判断是否有环

1.直接快慢指针，快指针会在环中兜圈会和慢指针相遇。

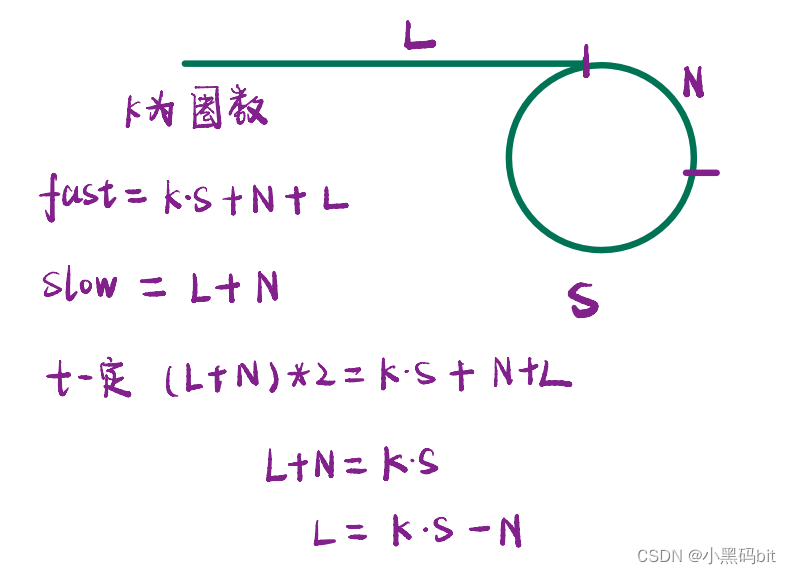
2.相遇的条件取决于两者的速度，这样就变成了一个数学的逻辑问题，如何制造相遇呢，假设slow一次走1步，fast一次走2步，入环前长度为L，环的长度为S，那么他们都差距步是一个2-1，4-2， 6-3，是一个顺序序列。那么当他们的差距步刚好为L+S时，就会相遇，所以如果有环他们迟早会相遇。

那么我们让fast一走3.4.5步又是什么情况呢，刚刚是通过差距步来判断的，现在同样如果fast一次走3步，那么差距步就是3-1,6-2,9-3是一个偶序列，最终如果(L+S )不是偶数或许永远不存在相遇。

判断环的入口

1.利用上面的参数，那么我们入环的入口就是L处，假设入口处与相遇处相差N

2. k是因为我们并不知道快指针走的圈数所以假设的值，但从图中我们可以得出相遇处到入口处S-N.

3.那么我们先走S-N将会到达入口处，其余走的都是整圈也就是我们定义一个meet再相遇处，一个origin在起始处，两者最终将会在入口处相遇。

step2:书写代码

判断是否有环

bool hasCycle(struct ListNode *head) {struct ListNode *fast=head;struct ListNode *slow=head;//如果没有环while(fast&&fast->next){slow=slow->next;fast=fast->next->next;if(slow==fast){return true;}}return false;}

判断环的入口

struct ListNode *detectCycle(struct ListNode *head) {struct ListNode *fast=head;struct ListNode *slow=head;//如果没有环while(fast&&fast->next){slow=slow->next;fast=fast->next->next;if(slow==fast){struct ListNode *meet=slow;struct ListNode *origin=head; while(meet!=origin){meet=meet->next;origin=origin->next;}return meet;}}return NULL;}