基础操作:
matlab命令行操作:
matlab可以使用命令行执行程序,例如下图运行后在右边工作区会产生响应的变量,如不写分号,则会直接运行。

- clear命令:clear用于清除变量。
- clc命令:clc用于清屏。
matlab编写脚本
新建脚本运行matlab程序,对比命令行操作更方便,对应的脚本后缀为.m
matlab默认变量名:
| ans | 最近一次运行结果 |
| eps | 浮点数的相对误差 |
| i,j | 虚数单位 |
| Inf | 表示无穷大 |
| NaN | 代表不定值,也就是不是数字 |
| pi | 圆周率 |
简单的赋值判断运算:
a = 5;%定义a为5
b = 2;%定义b为2
c = a > b;%a > b返回逻辑值1,逻辑值1赋值给c
d = a~= b;%a 不等于 b返回逻辑值1,逻辑值1赋值给d输入字符:
%input接收用户输入字符
x=input('请输入数字');
y=x*2;
y进阶操作
向量:
创建向量:
在matlab中,可以将数组,向量,矩阵,理解为一个东西,具体需要解决什么问题再细分为向量或矩阵或数组,创建向量时,逗号与分号等价,分号用于换行,如下程序:
a=[1 2 3 4 5];
b = [1, 2, 3, 4, 5];%与a等价
c=[6 7 8; 9 10 11];%二维矩阵
a
b
c还可以用另一种方式创建向量:
x = 2 : 2: 10;
这表示从2开始,步长为2,终点为10的向量。也就是x = [2, 4, 6, 8, 10]。
向量运算:
矩阵点积运算,也就是各个元素相乘。
a=[1 2 3 4 5];
b=[6 7 8 9 10];
c=a.*b
sum(c)%c所有元素之和向量的叉乘运算:(三维向量)


a=[1 2 3 ];
b=[6 7 8 ];
c=cross(a,b)%计算a,b的叉积从拉普拉斯角度计算:

使用拉普拉斯在第一行展开:
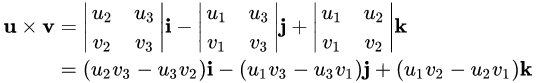
分支语句:
Matlab的分支结构语法为:
if 表达式执行语句
end
例1:使用if比较a,b的大小:
a = 2;
b = 1;
if a > bfprintf("a大于b");
end例2:使用if-else语句
a = 1;
b = 2;
if a > bfprintf("a大于b");
elsefprintf("a小于b");
end例3:使用if-elif语句
a = 1;
b = 1;
if a > bfprintf("a大于b");
elseif a == bfprintf("a等于b");
end例4:分支嵌套语句:
a = 4;
b = 1;
if a > bfprintf("a大于b,");if rem(a,2) == 0%取余运算fprintf("a是偶数");end
end循环结构:
for循环
for循环格式为:
for 变量 = 表达式循环体
end通常采用这种格式for 变量 = 开始值:步长:结束值
代码如下:
for a = 1:2:10 fprintf('第 %d次循环 \n', a);
end步长若不写,那么默认为1。
表达式为向量:
for a = [2 3 4 5 6]fprintf('第 %d次循环 \n', a);
end
while循环
while循环语句格式:
while 表达式循环体
end
例:实现1到100的累加和
i=1;
sum=0;
while(i<=100)sum=sum+i;i=i+1;
end
fprintf('1到100的累加和为: %d \n', sum);函数:
普通函数基本结构:
function 输出形参表 = 函数名(输入形参表)函数体语句
end
编写一个函数:
新建文件命名为MyMethod.m
function y= MyMethod(x)
% x为一个整数
if x>0y=2*x;
elseif x==0y=0;
elsey=x^2;
end
disp(y)
end运行时在命令行输入:MyMethod(2)即可
例2匿名函数:
f = @(变量列表)表达式
close all;
clc;
b=@(x)(sin(x)+cos(x)); %创建关于x的匿名函数
c=b(pi) %带入pi
d=@(x,y)(sin(x)+cos(y)) %创建x和y的匿名函数
e=d(pi,pi) %带入pi值测试建立矩阵函数:
| ones(n) | 建立一个n×n的1矩阵 |
| ones(m,n,……,p) | 建立一个m×n×……×p的1矩阵 |
| ones(size(A)) | 建立一个和矩阵A同样大小的1矩阵 |
| zeros(n) | 建立一个n×n的0矩阵 |
| zeros(m,n,……,p) | 建立一个m×n×……×p的0矩阵 |
| zeros(size(A)) | 建立一个和矩阵A同样大小的0矩阵 |
| eye(n) | 建立一个n×n的单位矩阵 |
| eye(m,n) | 建立一个m×n的单位矩阵 |
| eye(size(A)) | 建立一个和矩阵A同样大小的单位矩阵 |
随机数函数:
| rand | 产生在0~1之间均匀分布的随机数;每调用一次给一个新的数值 |
| rand + i*rand | 产生一个复数随机数 |
| rand(n) | 产生一个n×n的矩阵,其元素均为0~1之间均匀分布的随机数 |
| rand(m,n,……,p) | 产生一个m×n×……×p的矩阵,其元素均为0~1之间均匀分布的随机数 |
| randn | 产生零均值、单位方差的正太分布随机数 |
| randn(m,n,……,p) | 产生一个m×n×……×p的矩阵, 其元素均为零均值、单位方差的正太分布随机数 |













![[c++] 自写 MyString 类](http://pic.xiahunao.cn/[c++] 自写 MyString 类)



---Python中进程的Queue 和进程锁,以及进程池的创建 (包含详细注释代码))

