目录
- 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
- 第三周:浅层神经网络(Shallow neural networks)
- 3.6 激活函数(Activation functions)
- 3.7 为什么需要非线性激活函数?(why need a nonlinear activation function?)
- 3.8 激活函数的导数(Derivatives of activation functions)
第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)
第三周:浅层神经网络(Shallow neural networks)
3.6 激活函数(Activation functions)
使用一个神经网络时,需要决定使用哪种激活函数用隐藏层上,哪种用在输出节点上。到目前为止,之前的视频只用过 sigmoid 激活函数,但是,有时其他的激活函数效果会更好。
在神经网路的前向传播中, a [ 1 ] = σ ( z [ 1 ] ) a^{[1]}= σ(z^{[1]}) a[1]=σ(z[1])和 a [ 2 ] = σ ( z [ 2 ] ) a^{[2]} = σ(z^{[2]}) a[2]=σ(z[2])这两步会使用到sigmoid函数。sigmoid 函数在这里被称为激活函数。
公式 3.18: a = σ ( z ) = 1 1 + e − z a = σ(z) =\frac{1}{1+e^{-z}} a=σ(z)=1+e−z1
更通常的情况下,使用不同的函数 g ( z [ 1 ] ) g(z^{[1]}) g(z[1]),g可以是除了 sigmoid 函数意外的非线性函数。tanh 函数或者双曲正切函数是总体上都优于 sigmoid 函数的激活函数。如图,a= tan(z)的值域是位于+1 和-1 之间。
公式 3.19: a = t a n h ( z ) = e z − e − z e z + e − z a = tanh(z) =\frac{e^z−e^{-z}}{e^z+e^{-z}} a=tanh(z)=ez+e−zez−e−z
事实上,tanh 函数是 sigmoid 的向下平移和伸缩后的结果。对它进行了变形后,穿过了(0,0)点,并且值域介于+1 和-1 之间。
结果表明,如果在隐藏层上使用函数公式 3.20: g ( z [ 1 ] ) = t a n h ( z [ 1 ] ) g(z^{[1]}) = tanh(z^{[1]}) g(z[1])=tanh(z[1]) 效果总是优于 sigmoid 函数。因为函数值域在-1 和+1的激活函数,其均值是更接近零均值的。在训练一个算法模型时,如果使用 tanh 函数代替sigmoid 函数中心化数据,使得数据的平均值更接近 0 而不是 0.5.
在讨论优化算法时,有一点要说明:我基本已经不用 sigmoid 激活函数了,tanh 函数在所有场合都优于 sigmoid 函数。但有一个例外:在二分类的问题中,对于输出层,因为𝑦的值是 0 或 1,所以想让 y ^ \hat{y} y^的数值介于 0 和 1 之间,而不是在-1 和+1 之间。所以需要使用 sigmoid 激活函数。
这里的公式 3.21: g ( z [ 2 ] ) = σ ( z [ 2 ] ) g(z^{[2]}) = σ(z^{[2]}) g(z[2])=σ(z[2])在这个例子里看到的是,对隐藏层使用 tanh 激活函数,输出层使用 sigmoid 函数。
所以,在不同的神经网络层中,激活函数可以不同。为了表示不同的激活函数,在不同的层中,使用方括号上标来指出𝑔上标为[1]的激活函数,可能会跟𝑔上标为[2]不同。方括号上标[1]代表隐藏层,方括号上标[2]表示输出层。
sigmoid 函数和 tanh 函数两者共同的缺点是,在𝑧特别大或者特别小的情况下,导数的梯度或者函数的斜率会变得特别小,最后就会接近于 0,导致降低梯度下降的速度。
在机器学习另一个很流行的函数是:修正线性单元的函数(ReLu),ReLu 函数图像是如下图。 公式 3.22: 𝑎 = 𝑚𝑎𝑥(0, 𝑧) 所以,只要𝑧是正值的情况下,导数恒等于 1,当𝑧是负值的时候,导数恒等于 0。从实际上来说,当使用𝑧的导数时,𝑧=0 的导数是没有定义的。但是当编程实现的时候,𝑧的取值刚好等于 0.00000001,这个值相当小,所以,在实践中,不需要担心这个值,𝑧是等于 0 的时候,假设一个导数是 1 或者 0 效果都可以。
这有一些选择激活函数的经验法则:如果输出是 0、1 值(二分类问题),则输出层选择 sigmoid 函数,然后其它的所有单元都选择 Relu 函数。
这是很多激活函数的默认选择,如果在隐藏层上不确定使用哪个激活函数,那么通常会使用 Relu 激活函数。有时,也会使用 tanh 激活函数,但 Relu 的一个优点是:当𝑧是负值的时候,导数等于 0。
这里也有另一个版本的 Relu 被称为 Leaky Relu。当𝑧是负值时,这个函数的值不是等于 0,而是轻微的倾斜,如图。这个函数通常比 Relu 激活函数效果要好,尽管在实际中 Leaky ReLu 使用的并不多。
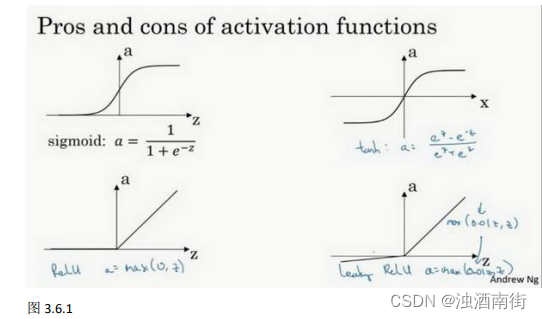
两者的优点是:
第一,在𝑧的区间变动很大的情况下,激活函数的导数或者激活函数的斜率都会远大于0,在程序实现就是一个 if-else 语句,而 sigmoid 函数需要进行浮点四则运算,在实践中,使用 ReLu 激活函数神经网络通常会比使用 sigmoid 或者 tanh 激活函数学习的更快。
第二,sigmoid 和 tanh 函数的导数在正负饱和区的梯度都会接近于 0,这会造成梯度弥散,而 Relu 和 Leaky ReLu 函数大于 0 部分都为常数,不会产生梯度弥散现象。(同时应该注意到的是,Relu 进入负半区的时候,梯度为 0,神经元此时不会训练,产生所谓的稀疏性,而 Leaky ReLu 不会有这问题)
𝑧在 ReLu 的梯度一半都是 0,但是,有足够的隐藏层使得 z 值大于 0,所以对大多数的训练数据来说学习过程仍然可以很快。
快速概括一下不同激活函数的过程和结论:
sigmoid 激活函数:除了输出层是一个二分类问题基本不会用它。
tanh 激活函数:tanh 是非常优秀的,几乎适合所有场合。
ReLu 激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用 ReLu 或者Leaky ReLu。
公式 3.23: 𝑎 = 𝑚𝑎𝑥(0.01𝑧, 𝑧)
为什么常数是 0.01?当然,可以为学习算法选择不同的参数。
在选择自己神经网络的激活函数时,有一定的直观感受,在深度学习中的经常遇到一个问题:在编写神经网络的时候,会有很多选择:隐藏层单元的个数、激活函数的选择、初始化权值……这些选择想得到一个对比较好的指导原则是挺困难的。
鉴于以上三个原因,以及在工业界的见闻,提供一种直观的感受,哪一种工业界用的多,哪一种用的少。但是,自己的神经网络的应用,以及其特殊性,是很难提前知道选择哪些效果更好。所以通常的建议是:如果不确定哪一个激活函数效果更好,可以把它们都试试,然后在验证集或者发展集上进行评价。然后看哪一种表现的更好,就去使用它。
为自己的神经网络的应用测试这些不同的选择,会在以后检验自己的神经网络或者评估算法的时候,看到不同的效果。如果仅仅遵守使用默认的 ReLu 激活函数,而不要用其他的激励函数,那就可能在近期或者往后,每次解决问题的时候都使用相同的办法。
3.7 为什么需要非线性激活函数?(why need a nonlinear activation function?)
为什么神经网络需要非线性激活函数?事实证明:要让你的神经网络能够计算出有趣的函数,你必须使用非线性激活函数,证明如下:
这是神经网络正向传播的方程,现在我们去掉函数g,然后令 a [ 1 ] = z [ 1 ] a^{[1]}= z^{[1]} a[1]=z[1],或者我们也可以令g(z) = z,这个有时被叫做线性激活函数(更学术点的名字是恒等激励函数,因为它们就是把输入值输出)。为了说明问题我们把 a [ 2 ] = z [ 2 ] a^{[2]} = z^{[2]} a[2]=z[2],那么这个模型的输出𝑦或仅仅只是输入特征𝑥的线性组合。
如果我们改变前面的式子,令:
(1) a [ 1 ] = z [ 1 ] = W [ 1 ] x + b [ 1 ] a^{[1]} = z^{[1]} = W^{[1]}x + b^{[1]} a[1]=z[1]=W[1]x+b[1]
(2) a [ 2 ] = z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ] a^{[2]} = z^{[2]} = W^{[2]}a^{[1]} + b^{[2]} a[2]=z[2]=W[2]a[1]+b[2]
将式子 (1) 代 入 式 子 (2) 中 , 则 : a [ 2 ] = z [ 2 ] = W [ 2 ] ( W [ 1 ] x + b [ 1 ] ) + b [ 2 ] a^{[2]} = z^{[2]} =W^{[2]}(W^{[1]}x + b^{[1]}) + b^{[2]} a[2]=z[2]=W[2](W[1]x+b[1])+b[2]
(3) a [ 2 ] = z [ 2 ] = W [ 2 ] W [ 1 ] x + W [ 2 ] b [ 1 ] + b [ 2 ] a^{[2]} = z^{[2]} = W^{[2]}W^{[1]}x + W^{[2]}b^{[1]} + b^{[2]} a[2]=z[2]=W[2]W[1]x+W[2]b[1]+b[2]
简化多项式得 a [ 2 ] = z [ 2 ] = W ′ x + b ′ a^{[2]} = z^{[2]} = W'x + b' a[2]=z[2]=W′x+b′
如果你是用线性激活函数或者叫恒等激励函数,那么神经网络只是把输入线性组合再输出。
我们稍后会谈到深度网络,有很多层的神经网络,很多隐藏层。事实证明,如果你使用线性激活函数或者没有使用一个激活函数,那么无论你的神经网络有多少层一直在做的只是计算线性函数,所以不如直接去掉全部隐藏层。在我们的简明案例中,事实证明如果你在隐藏层用线性激活函数,在输出层用 sigmoid 函数,那么这个模型的复杂度和没有任何隐藏层的标准 Logistic 回归是一样的,如果你愿意的话,可以证明一下。
在这里线性隐层一点用也没有,因为这两个线性函数的组合本身就是线性函数,所以除非你引入非线性,否则你无法计算更有趣的函数,即使你的网络层数再多也不行;只有一个地方可以使用线性激活函数------𝑔(𝑧) = 𝑧,就是你在做机器学习中的回归问题。𝑦 是一个实数,举个例子,比如你想预测房地产价格,𝑦 就不是二分类任务 0 或 1,而是一个实数,从0 到正无穷。如果𝑦 是个实数,那么在输出层用线性激活函数也许可行,你的输出也是一个实数,从负无穷到正无穷。
总而言之,不能在隐藏层用线性激活函数,可以用 ReLU 或者 tanh 或者 leaky ReLU 或者其他的非线性激活函数,唯一可以用线性激活函数的通常就是输出层;除了这种情况,会在隐层用线性函数的,除了一些特殊情况,比如与压缩有关的,那方面在这里将不深入讨论。在这之外,在隐层使用线性激活函数非常少见。因为房价都是非负数,所以我们也可以在输出层使用 ReLU 函数这样你的𝑦^都大于等于 0。
理解为什么使用非线性激活函数对于神经网络十分关键,接下来我们讨论梯度下降,并在下一个视频中开始讨论梯度下降的基础——激活函数的导数。
3.8 激活函数的导数(Derivatives of activation functions)
在神经网络中使用反向传播的时候,你真的需要计算激活函数的斜率或者导数。针对以下四种激活,求其导数如下:
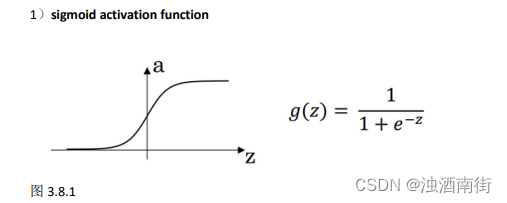
其具体的求导如下:
公式 3.25:
d d z g ( z ) = 1 1 + e − z ( 1 − 1 1 + e − z ) = g ( z ) ( 1 − g ( z ) ) \frac{d}{dz}g(z)=\frac{1}{1+e^{-z}}(1 −\frac{1}{1+e^{-z}}) = g(z)(1−g(z)) dzdg(z)=1+e−z1(1−1+e−z1)=g(z)(1−g(z))
注:
当z = 10 或z= −10 d d z g ( z ) \frac{d}{dz}g(z) dzdg(z) ≈ 0; 当z= 0 d d z g ( z ) = g ( z ) ( 1 − g ( z ) ) \frac{d}{dz}g(z)= g(z)(1 − g(z)) dzdg(z)=g(z)(1−g(z)) = 1/4
在神经网络中 a = g(z); g(z)′ = d d z g ( z ) = a ( 1 − a ) \frac{d}{dz}g(z) =a(1 − a) dzdg(z)=a(1−a)
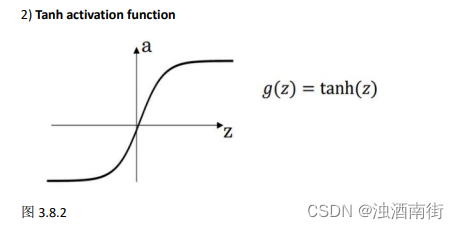
其具体的求导如下:
公式 3.26: g ( z ) = t a n h ( z ) = e z − e − z e z + e − z g(z) =tanh(z) =\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} g(z)=tanh(z)=ez+e−zez−e−z
公式 3.27: d d z g ( z ) = 1 − ( t a n h ( z ) ) 2 \frac{d}{dz}g(z) =1 -(tanh(z))^2 dzdg(z)=1−(tanh(z))2
注:
当𝑧 = 10 或𝑧 = −10 d d z g ( z ) \frac{d}{dz}g(z) dzdg(z) ≈ 0; 当𝑧 = 0, d d z g ( z ) \frac{d}{dz}g(z) dzdg(z) = 1 − (0) = 1;
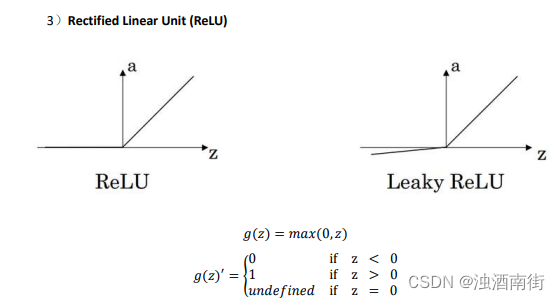
注:通常在𝑧= 0 的时候给定其导数 1,0;当然𝑧=0 的情况很少
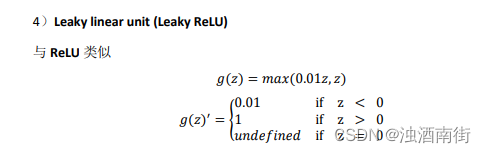
注:通常在𝑧 = 0的时候给定其导数 1,0.01;当然𝑧 = 0的情况很少












)





--SpringCloud简介)
