引言
状态空间方程是现代控制理论的基础,它以矩阵的形式表达系统的状态变量,输入及输出的关系。它可以描述和处理多输入多输出的系统。
目前流行的一些算法,比如:模型预测控制、卡尔曼滤波器及最优化控制都是在状态空间方程的表达形式基础上发展而来的。
状态空间方程
状态空间方程表达式
- 我们可以从如下这个例子入手,下面是一个弹簧质量阻尼系统:
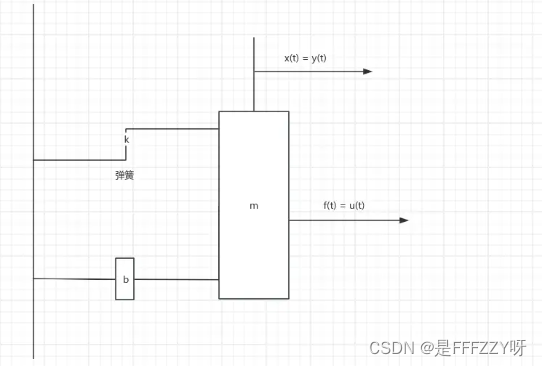
- 它的动态微分方程为:

- 其中:x(t)是位移,方向向右;m是质量;b是阻尼系数,k是弹簧系数;f(t)就表示外力
- 我们对于等式的两边同时进行拉普拉斯变换,并将u(t)=f(t)、y(t) = x(t)代入进行调整,并且同时假定零初始条件为:
- 那么这样可以得到系统的传递函数为:
- 对应的系统框图如图所示:
- 对于同样的系统,在现代控制理论中,会采取状态空间方程的表达方式。
- 状态空间方程是一个集合,它包含了系统的输入、输出以及状态变量,并把他们用一系列的一阶微分方程表达出来。
- 对于上述的二阶系统,为了将其写成状态空间方程,我们需要选取合适的空间变量,才能使二阶系统转换为一些列的一阶系统:
- 选取两个状态变量:
 (式1)
(式1)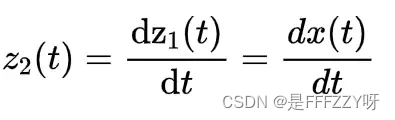
- 代入上述的微分方程中可以得到:

 (式2)
(式2)
- 接下来,我们就可以把式1和式2联合起来,写成一个紧凑的矩阵表达形式:
 (式 3)
(式 3)
- 系统的输出y(t) = x(t)也可以写成矩阵的形式:
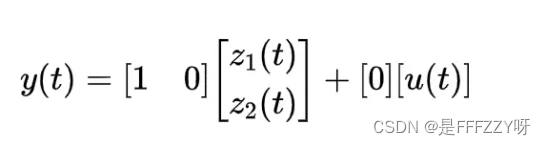 (式 4)
(式 4)
- 上面的式3和式4就是弹簧质量阻尼系统的状态空间方程
- 选取两个状态变量:
上面的形式可以推广到状态空间方程的一般形式,也就是:
其中:
- z(t)是状态变量,是一个n维向量
- y(t)是系统输出,是一个m维向量
- u(t)是系统输入,是p维向量
这样也就说明:
- 当使用状态空间方程来描述系统时,有n个状态变量,m个输出和p个输入。
- 它可以表示多状态、多输出、多输入的系统。
- A是一个n×n的矩阵,表示系统状态变量之间的关系,称为状态矩阵或系统矩阵。
- B是一个n×p的矩阵,表示输入对状态之间的影响,称为输入矩阵或者控制矩阵
- C是一个m×n的矩阵 ,表示系统的输入与系统状态变量之间的关系,称为输出矩阵
- D是一个m×p的矩阵,表示系统的输入直接作用在系统输出的部分,称为直接传递矩阵
单输入单输出矩阵
在上述的系统中,系统的输出是y(t) = x(t),是一个m=1维向量,输入u(t) = f(t)表示也是一维向量,所以是一个单输入单输出系统。
多输入多输出矩阵
- 下面是一个多输入、多输出矩阵的例子,电路网络系统:
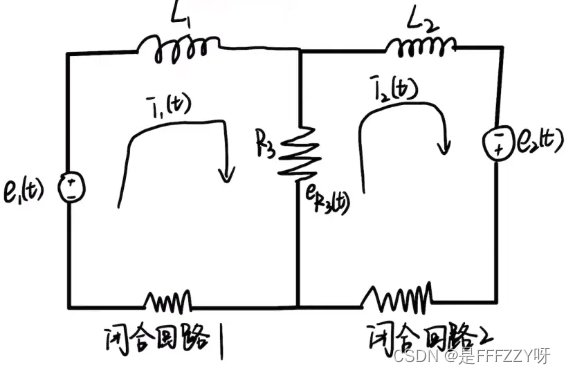
- 此时系统中有两个输入和两个输出,分别是:
- 输入:
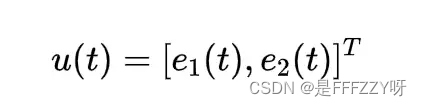
- 输出:
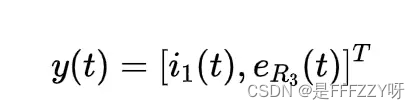
- 输入:
- 如果我们需要建立上述系统的状态空间方程,那么就需要先掌握它的动态微分方程。那么这个系统就可以考虑成两个闭合的回路,在每一个闭合回路中使用基尔霍夫电压定律,那么就可以得到:
- 闭合回路1:
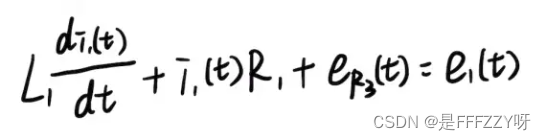 (式5)
(式5) - 闭合回路2:
 (式6)
(式6) - 其中:
 (式7)
(式7) - 那我们再把式7带入到(式5和式6)中,进行化简,可以得到:
 ( 式 8)
( 式 8) (式 9)
(式 9)
- 选取系统的状态变量
 ,其中:
,其中: - 将状态变量,带入到(式 8)和(式 9)中,可以得到:
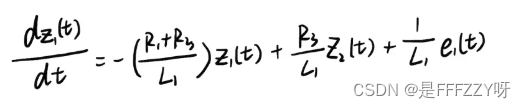 (式 10)
(式 10) (式 11)
(式 11)
- 将式11 和式 12 写成紧凑的矩阵的形式,得到:
- 系统输出
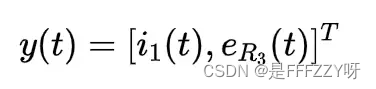 ,可以表达为:
,可以表达为: - 将上面两个式子,写成一般表达式,就可以得到状态空间方程的,即:
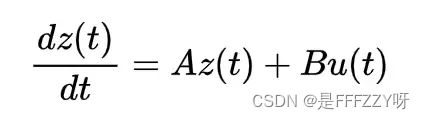
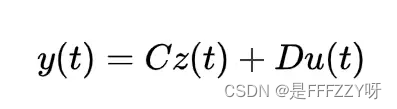
- 其中:
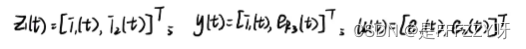
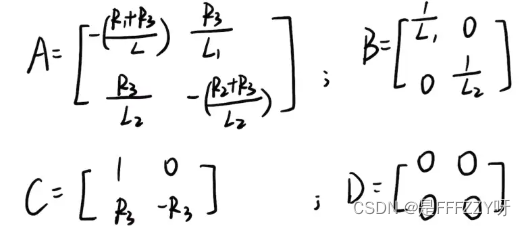
- 闭合回路1:
状态空间与传递函数之间的关系
- 对于空间状态方程的等号两边,同时做拉普拉斯变换,我们可以得到:
- 考虑其零初始状态,我们可以得到如下的式子:
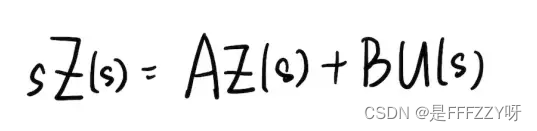 (式 12)
(式 12) (式 13)
(式 13)
- 对于式12调整之后,我们可以得到:
 (式 14)
(式 14) - 其中,I表示的是一个n×n的单位矩阵
- 我们把式14带入到式13中进行调整,我们可以得到:
- 这样,我们就可以得到传递函数的表达式为:
- 同时,我们再考虑弹簧质量的阻尼系统,其中D=0,根据矩阵求逆公式,带入上述式子中,可以得到:
- 我们可以观察到上面的这个公式,如果分母部分为0,那么也就是行列式值为0,得出来的s的值就有两个含义:
- 第一、从传递函数的角度考虑,他是传递函数的极点
- 第二、从状态矩阵的角度考虑,它是矩阵A的特征值
- 那么根据上面的两点,我们就可以做出判断:当我们把当前系统写成状态空间方程之后,状态矩阵A的特征值即为其对应的传递函数G(s)的极点。

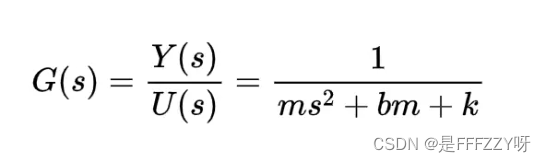
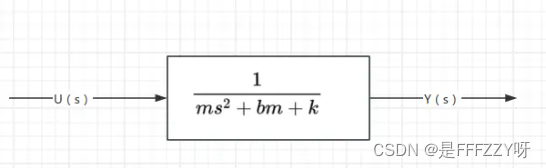



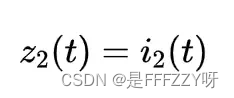

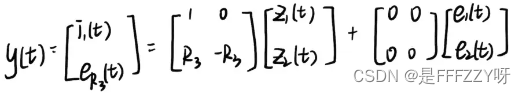

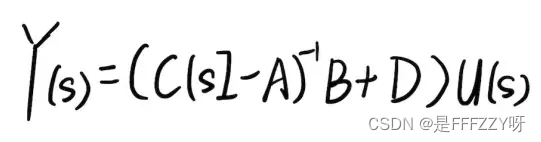

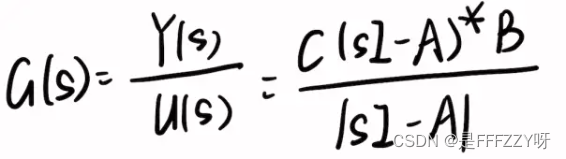




Springboot的纹理生产图片系统(有论文))


)



)



)


)
