2016年认证杯SPSSPRO杯数学建模
C题 如何有效的抑制校园霸凌事件的发生
原题再现:
近年来,我国发生的多起校园霸凌事件在媒体的报道下引发了许多国人的关注。霸凌事件对学生身体和精神上的影响是极为严重而长远的,因此对于这些情况我们应该给予高度的重视。霸凌是各种形式校园暴力中的一种,从某种意义上说,也是危害程度较高的一种。不同于偶发的暴力事件,霸凌行为通常伴随着肉体与精神的双重伤害,并且这种伤害通常会持续很长时间,有时可能会对受害者的心灵产生终身创伤。如果没有受到专业的心理引导,受害者有可能转变为报复社会的人,进而从受害者转变为施暴者,将自己的遭遇原封不动或放大百倍地转嫁到他人身上。
2015 年 6 月 21 日,一段“小学生被多人围殴”的视频在网上广泛传播。据网民爆料,浙江省丽水市庆元县几名初中生把一名小学一年级的学生关在黑屋子里暴力殴打,并用香烟头烫伤小孩。6 月 21 日晚 8 时左右,著名演员陈坤在微博上转发了这一视频。媒体人“大鹏看天下”当晚也在微博上呼吁公安部门立即介入,“别再手软,此类事件必须严惩,结果广为通报!”多名网络“大 V”的关注,让这一事件迅速发酵为热点。不少网民震惊于视频中的情景,慨叹“校园霸凌现象竟严重至此”。
科学技术的飞速发展和互联网的普及,给青少年带来的不仅仅是积极的影响。很多初中生表示曾遭受手机、互联网上的谩骂、侮辱等新型暴力行为的影响。网络霸凌的暴力行为由于侮辱性信息传播速度快,因此造成了更直接的伤害。此外,信息扩散范围速度极快,往往来不及阻止信息的传播,也来不及保护学生,就已经对受害者造成了极大程度的伤害。
驱使青少年施加网络暴力行为的原因很多,但最主要的诱因还是年龄。青少年由于年龄较小,不够成熟,不知道如何应对和转化暴力性冲动,才造成对自身和他人的伤害。我们设计了一次针对不同年龄段青少年的心理状况的问卷调查,试图建立一个模型来判断青少年存在一些潜在心理问题的可能性。调查分为 5 个年龄段,这要涉及生命教育、生活方式、娱乐三个领域,分别包括正向和负向两个框架。其中因变量被设计成一种二选一式的评价变量,使用 A 或 B 来表示。自变量包括风险偏好、认知需要(包括 18 个题目)、决策风格(包括理智型、直觉型、依赖型、回避型、冲动型,这 5 个维度,每个维度下包括 5 个题目)三个主要方面,每个方面的题目可以按照选择的答案来计算相应的得分。调查的结果如附件一所示。
第二阶段问题:
3. 请你建立合理的数学模型,对于附件中的案例进行评价,评估案例中人物存在心理问题的风险。
4. 请你结合第一阶段的模型,建立一套青少年心理问题的预警机制,并结合实际的案例给出相应的解决方案。
整体求解过程概述(摘要)
近年来,世界各地频繁地发生校园霸凌事件,给学生、家长和学校等各方面带来了极大的危害,也引起了社会广泛的关注.想要有效的抑制校园霸凌,就要从根本上去解决问题,也就是需要从学生的心理问题着手处理.但是由于并不是每一个家长、老师都精通心理学,所以建立一个具有普适性、科学性的预警机制就十分必要.本文首先使用 EXCEL 和 SPSS 对附件所给数据进行了重组、格式转换、缺失值填充、标准化处理和剔除异常样本等处理,并运用K-means算法对各个年龄组的样本进行聚类,以检验数据预处理的结果是否可靠,为接下来的模型建立提供根本的数据保证.
针对问题一,本文建立了基于 TOPSIS 和灰色关联分析的风险指数模型,去评估附件所给案例的心理现状.该模型首先使用 R 型聚类分析确定了五个综合评价指标,通过熵权法客观地确定了各个指标的权重;然后分别通过 TOPSIS 和灰色关联分析两种方法求出风险指数k1和k2 ,其中k1为案例到正负理想解的距离之比,k2 为案例对正理想解的灰色加权关联度的倒数与 0.05 的乘积;最后为了得到最终的风险指数模型,随机选取 10 个样本对k1和k2进行对比,得到了k1和k2 两个风险指数的值基本一致、互不矛盾的结论,故可以定义最终的风险指数k = 0.5 *(k1 + k2).根据案例的风险指数值,本文将案例分成了存在心理问题的风险高、较高、中、较低、低五种类别.
针对问题二,根据第一阶段模型得到的六个框架均有四个主要影响因素的结论,本文首先建立了基于 BP 神经网络模型和 RBF 神经网络模型的两种心理预警机制,将每个框架的值视作输出变量,其主要影响因素视作对应的输入变量,通过两种神经网络模型分别进行对输出变量的预测,若六个输出变量的平均值大于 0.17,则对样本的心理问题进行预警;然后将两种模型输出的预测值进行对比,得到了 BP 神经网络预测值的平均相对误差更小的结论,进而将基于 BP 神经网络的心理问题预警机制当作最终的心理问题预警机制;在此基础之上,本文生成了 10 组随机数据对最终的预警机制进行模型仿真,检验出该模型是可以在实际中进行应用的;最后利用该预警机制与实际案例相结合,从附件样本中随机选取三个预测样本作为案例,给出相应的心理问题的解决方案.
考虑到收集数据的误差,本文对风险指数模型作了灵敏度分析,以检验模型的实用性.本文客观公正地描述了模型的优缺点,并对部分缺点提出了改进建议,以期待它们能被完善,并得到推广和应用.
问题分析:
问题一的分析
为了进行综合评价,本文用 R 型聚类分析筛选出 5 个指标,并用熵权法计算尺每个指标的权重.为了评价附件中每个案例存在心理问题的风险大小,首先,本文尝试通过理想解法,构造心理状况最好的、存在心理问题的风险最小的假想案例 1 和心理状况最差的、存在心理问题的风险最大的假想案例 2,即正理想解和负理想解,并将每个案例与正负理想解的距离之比视作其存在心理问题的风险指数 1 k .接着,本文尝试通过灰色关联分析法,计算出每个案例对正理想解的灰色加权关联度r ,并将0.05/r视作其存在心理问题的风险指数k2。最后可得每个案例的风险指数为
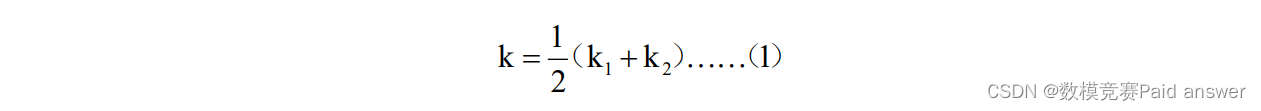
问题二的分析
通过查阅文献可以知道,针对同一个问题时个体会同时有正向和负向两种看法与心态,只是各自程度不同.而对于同一问题,无论正负向框架,评价 A 和 B 都是指个体的心理状况的同一倾向.[3] 将 A 当作个体心理状况正常的倾向,B 当作个体心理状况异常的倾向,由于框架值为 A 时的标准化后的数据值为-0.73,框架值为 B 时标准化后的数据值为 1.07,故当个体六个正负框架的得分的平均值大于 0.17 时,说明个体可能出现心理问题.
根据第一阶段的模型,影响生命教育正向框架的因素主要有风险偏好得分、直觉性得分、理智型得分和认知需要得分,影响生命教育负向框架的因素主要有风险偏好得分、直觉型得分、理智型得分和认知需要得分,影响生活方式正向框架的因素主要有风险偏好得分、理智型得分、依赖型得分和直觉型得分,影响生活方式负向框架的因素主要有风险偏好得分、回避型得分、冲动型得分和依赖型得分,影响娱乐正向框架的因素主要有风险偏好得分、回避型得分、冲动型得分和直觉型得分,影响娱乐负向框架的因素主要有风险偏好得分、依赖型得分、直觉型得分和冲动型得分.
为了建立青少年心理问题的预警机制,本文将六个正负框架值视为因变量,将其影响因素视为与其对应的自变量,构成六个网络,每个网络均有 4 个输入神经元和 1 个输出神经元.将部分样本的数据作为训练样本集,其余样本的数据作为预测检验样本,建立 BP 神经网络和 RBF 神经网络模型,对比两个模型的预测结果误差,选取平均误差小的模型作为最后的预测模型.对于一个新的青少年样本,可根据其输入变量的相关数据对输出变量进行预测,当六个预测结果的平均值大于 0.17 时,即提出预警,表示该青少年心理很可能出现问题.
模型假设:
1.假设附件中的数据真实可靠;
2.假设除风险偏好、认知需求、决策风格外的其他因素对生命教育、生活方式、娱乐的正负框架的影响可以忽略;
3.假设人在 20 岁之后心理已经稳定,不会发生较大突变;
4.假设题中所给数据对应的青少年样本是真实存在的;
5.假设 R 型聚类后,属于不同类别的指标之间相互独立;
6.假设在进行青少年心理问题预警时,生命教育正负向框架、生活方式正负向框架和娱乐方式正向框架的重要性是相同的,即在这里不考虑各个框架的权重对预警结果的影响.
论文缩略图:



全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
k=4;
x =[]; %数据
[n,d] = size(x);
bn=round(n/k*rand);%第一个随机数在前 1/K 的范围内
%;表示按列显示,都好表示按行显示
nc=[x(bn,:);x(2*bn,:);x(3*bn,:);x(4*bn,:)];%初始聚类中心
%x(bn,:) 选择某一行数据作为聚类中心,其列值为全部
%x 数据源,k 聚类数目,nc 表示 k 个初始化聚类中心
%cid 表示每个数据属于哪一类,nr 表示每一类的个数,centers 表示聚类中心
[cid,nr,centers] = kmeans(x,k,nc)%调用 kmeans 函数
%认为不该是 150,或者说不该是个确定值,该是 size(x,1)就是 x 行数
for i=1:150if cid(i)==1, plot(x(i,1),x(i,2),'r*') % 显示第一类%plot(x(i,2),'r*') % 显示第一类hold on elseif cid(i)==2, plot(x(i,1),x(i,2),'b*') %显示第二类% plot(x(i,2),'b*') % 显示第一类hold on elseif cid(i)==3, plot(x(i,1),x(i,2),'g*') %显示第三类% plot(x(i,2),'g*') % 显示第一类hold on elseif cid(i)==4, plot(x(i,1),x(i,2),'k*') %显示第四类% plot(x(i,2),'k*') % 显示第一类
hold on end end end end
end
strt=['红色*为第一类;蓝色*为第二类;绿色*为第三类;黑色*为第四类' ];
text(-4,-3.6,strt);
%x 数据源,k 聚类数目,nc 表示 k 个初始化聚类中心
%cid 表示每个数据属于哪一类,nr 表示每一类的个数,centers 表示聚类中心
function [cid,nr,centers] = kmeans(x,k,nc) [n,d] = size(x); % 设置 cid 为分类结果显示矩阵cid = zeros(1,n); % Make this different to get the loop started. oldcid = ones(1,n); % The number in each cluster. nr = zeros(1,k); % Set up maximum number of iterations. maxgn= 100; iter = 1; %计算每个数据到聚类中心的距离 ,选择最小的值得位置到 cidwhile iter < maxgn for i = 1:n %repmat 即 Replicate Matrix ,复制和平铺矩阵,是 MATLAB 里面的一
个函数。%B = repmat(A,m,n)将矩阵 A 复制 m×n 块,即把 A 作为 B 的元素,B
由 m×n 个 A 平铺而成。B 的维数是 [size(A,1)*m, size(A,2)*n] 。%点乘方 a.^b,矩阵 a 中每个元素按 b 中对应元素乘方或者 b 是常数%sum(x,2)表示矩阵 x 的横向相加,求每行的和,结果是列向量。 而缺省
的 sum(x)就是竖向相加,求每列的和,结果是行向量。dist = sum((repmat(x(i,:),k,1)-nc).^2,2); [m,ind] = min(dist); % 将当前聚类结果存入 cid 中cid(i) = ind; end %找到每一类的所有数据,计算他们的平均值,作为下次计算的聚类中心for i = 1:k %find(A>m,4)返回矩阵 A 中前四个数值大于 m 的元素所在位置ind = find(cid==i); %mean(a,1)=mean(a)纵向;mean(a,2)横向nc(i,:) = mean(x(ind,:)); %统计每一类的数据个数nr(i) = length(ind); end iter = iter + 1;
end % Now check each observation to see if the error can be minimized some
more. % Loop through all points. maxiter = 2;iter = 1; move = 1; %j~=k 这是一个逻辑表达式,j 不等于 k,如果 j 不等于 k,返回值为 1,否则为 0while iter < maxiter & move ~= 0 move = 0; %对所有的数据进行再次判断,寻求最佳聚类结果for i = 1:n dist = sum((repmat(x(i,:),k,1)-nc).^2,2); r = cid(i); % 将当前数据属于的类给 r %点除,a.\b 表示矩阵 b 的每个元素除以 a 中对应元素或者除以常数 a,a.
/b 表示常数 a 除以矩阵 b 中每个元素或者矩阵 a 除以矩阵 b 对应元素或者常数 b%nr 是没一类的的个数%点乘(对应元素相乘),必须同维或者其中一个是标量,a.*bdadj = nr./(nr+1).*dist'; % 计算调整后的距离[m,ind] = min(dadj); % 找到该数据距哪个聚类中心最近if ind ~= r % 如果不等则聚类中心移动cid(i) = ind;%将新的聚类结果送给 cid ic = find(cid == ind);%重新计算调整当前类别的聚类中心nc(ind,:) = mean(x(ic,:)); move = 1; end end iter = iter+1; end centers = nc; if move == 0 disp('No points were moved after the initial clustering procedure.')elsedisp('Some points were moved after the initial clustering procedure.
') end
)


)
)


)











