目录
- 题目描述
- 解法
- 方法一:数组标记
- 方法二:原地标记
- 运行结果
- 方法一
- 方法二
题目描述
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
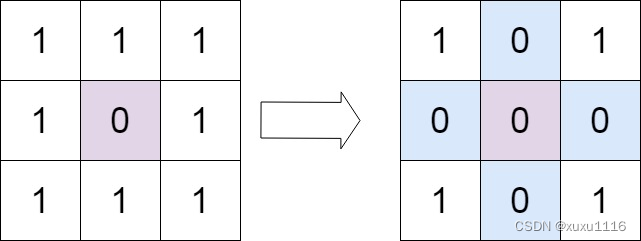
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
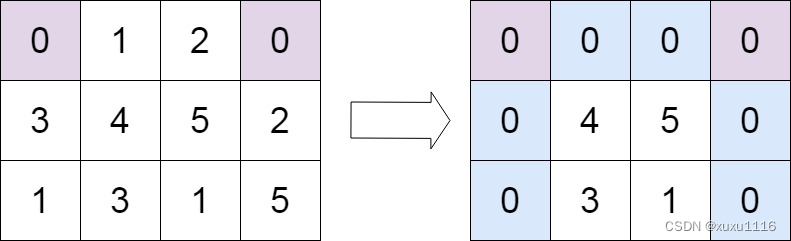
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
- m == matrix.length
- n == matrix[0].length
- 1 <= m, n <= 200
- -231 <= matrix[i][j] <= 231 - 1
解法
方法一:数组标记
我们分别用数组 rows 和 cols 标记待清零的行和列。
然后再遍历一遍矩阵,将 rows 和 cols 中标记的行和列对应的元素清零。
时间复杂度 O(m×n),空间复杂度 O(m+n)。其中 m 和 n 分别为矩阵的行数和列数。
class Solution(object):def setZeroes(self, matrix):""":type matrix: List[List[int]]:rtype: None Do not return anything, modify matrix in-place instead."""m, n = len(matrix), len(matrix[0])rows = [0] * mcols = [0] * nfor i, row in enumerate(matrix):for j, v in enumerate(row):if v == 0:rows[i] = cols[j] = 1for i in range(m):for j in range(n):if rows[i] or cols[j]:matrix[i][j] = 0
方法二:原地标记
方法一中使用了额外的数组标记待清零的行和列,实际上我们也可以直接用矩阵的第一行和第一列来标记,不需要开辟额外的数组空间。
由于第一行、第一列用来做标记,它们的值可能会因为标记而发生改变,因此,我们需要额外的变量 i0, j0 来标记第一行、第一列是否需要被清零。
时间复杂度 O(m×n),空间复杂度 O(1)。其中 m 和 n 分别为矩阵的行数和列数。
class Solution(object):def setZeroes(self, matrix):""":type matrix: List[List[int]]:rtype: None Do not return anything, modify matrix in-place instead."""m, n = len(matrix), len(matrix[0])i0 = any(v == 0 for v in matrix[0])j0 = any(matrix[i][0] == 0 for i in range(m))for i in range(1, m):for j in range(1, n):if matrix[i][j] == 0:matrix[i][0] = matrix[0][j] = 0for i in range(1, m):for j in range(1, n):if matrix[i][0] == 0 or matrix[0][j] == 0:matrix[i][j] = 0if i0:for j in range(n):matrix[0][j] = 0if j0:for i in range(m):matrix[i][0] = 0
运行结果
方法一
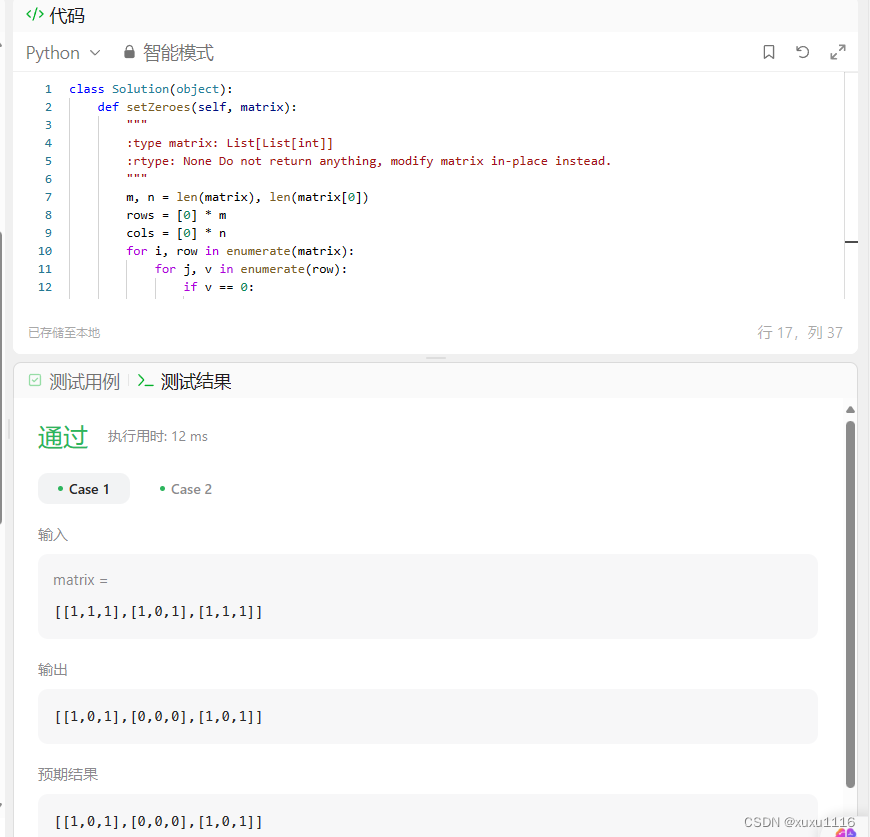
方法二
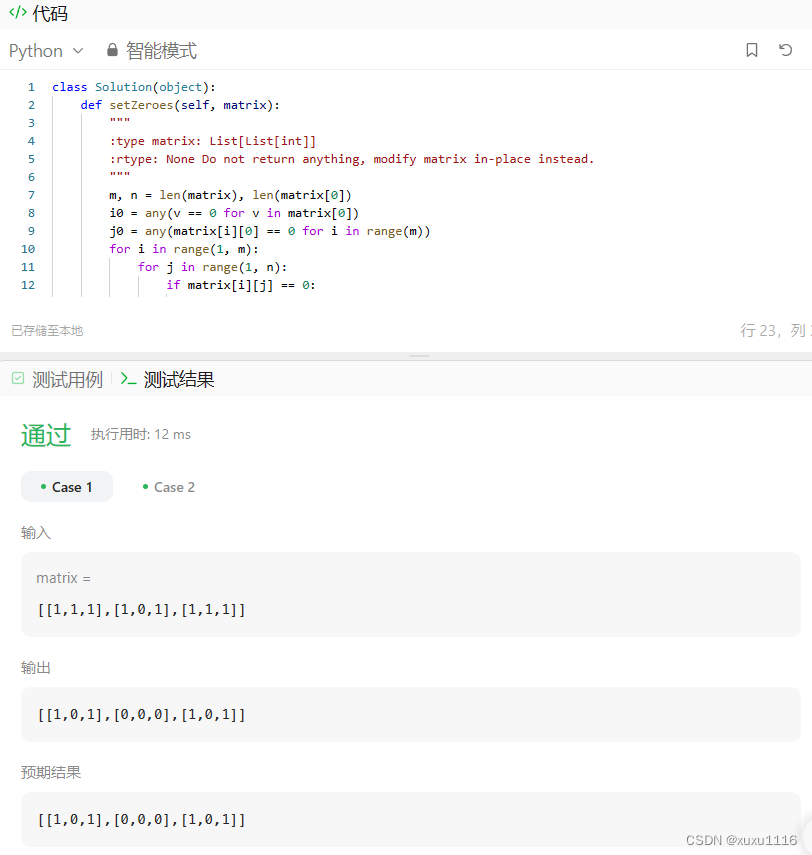





)


)

——以太网数据帧和DNS协议(数据链路层和应用层))
)

)
)




