理解混淆矩阵和ROC曲线之前，先区分几个概念。对于分类问题，不论是多分类还是二分类，对于某个关注类来说，都可以看成是二分类问题，当前的这个关注类为正类，所有其他非关注类为负类。因为样本的真实值有正负两类，而模型的预测值也有正负两类，因此样本的真实值和模型的预测值之间产生了下面4种组合：

• 真正例(True Positives/TP)：在所有真实值为正类的样本中，模型预测值也为正类的样本数。
• 假正例(False Positives/FP)：在所有真实值为负类的样本中，模型预测值为正类的样本数。
• 真负例(True Negatives/TN)：所有真实值为负类的样本中，模型预测值也为负类的样本数。
• 假负例(False Negatives/FN)：所有真实值为正类的样本中，模型预测值为负类的样本数。

从上面几个定义可以知道：
1）样本总数 = TP+FP+TN+FN
2）所有真实值为正类的样本总数 = TP+FN
3）所有真实值为负类的样本总数 = TN+FP

1.混淆矩阵

使用sklearn自带的鸢尾花数据集，数据集里鸢尾花包含3个分类。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix# 获取特征值与目标值
data = load_iris()
X, y = data['data'], data['target']# 自带的数据集分类准确率为1，为了后面更好的基于混淆矩阵验证相关指标的计算，为训练集添加均值0，标准差2的高斯噪声
np.random.seed(42)
noise = np.random.normal(0, 2, (len(X), len(X[0])))
X += noise# 特征值归一化到区间[-1,1]
scaler = MinMaxScaler(feature_range=(-1, 1))
X_scaled = scaler.fit_transform(X)# 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)# 创建逻辑回归模型、训练并预测
model = LogisticRegression(multi_class='multinomial', max_iter=1000)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)# 获取模型混淆矩阵、分类报告、准确率
print(f"混淆矩阵：\n{confusion_matrix(y_test, y_pred)}")
print(f"分类报告：\n{classification_report(y_test, y_pred)}")
print(f"准确率：\n{accuracy_score(y_test, y_pred)}")

output：

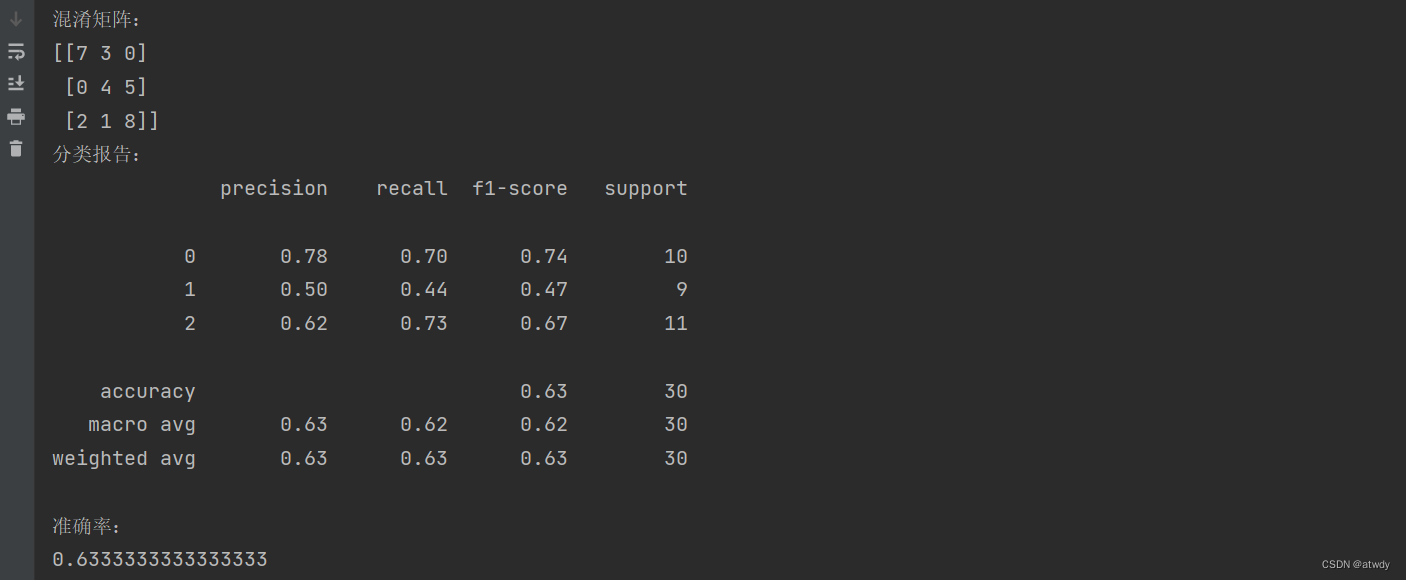
混淆矩阵中，横向表示真实值，纵向表示预测值。比如第一个位置7，表示实际类别为0且预测类别为0的样本有7个。基于此混淆矩阵，可以衍生下面相关指标：
1）准确率(accuracy)：准确率表示模型对一个样本类别预测正确的可能性，是相对整体来说的。计算方式为所有预测正确的样本（斜对角线之和）/ 样本总数，本例中accuracy=(7+4+8)/30=0.63…
2）精确率(precision)：精确率是针对某个具体关注类来说的，精确率关注的是，对于所有预测值为该类的样本中，真实值也属于该类的样本所占的比例，计算公式为$\frac{TP}{TP+FP}$。比如对于类别0，模型预测的该类样本数=(7+0+2)=9，而真实值为该类的样本数为7，那么类别0的precision=7/9=0.77…。精确率反映了“模型找的对不对”
3）召回率(recall)：同样召回率也是针对某个具体关注类来说的，关注的是所有真实值为该类的样本中，模型能正确预测为该类的样本所占的比例，计算公式$\frac{TP}{TP+FN}$。还是拿类别0来说，真实值为0的样本总数=(7+3+0)=10，模型能正确预测为该类的样本总数为7，所以类别0的召回率=7/10=0.7。召回率代表了“模型找的全不全”
4）F1-score：F1分数是精确率与召回率的调和平均数，计算公式为$\frac{2\ast precision\ast recall}{precision+recall}$。对于类别0的F1-score=$\frac{2\ast 0.78\ast 0.7}{0.78+0.7}$=0.737…，F1分数用来表示模型在关注的类上识别正类的综合表现，最大值1表示分类效果最好完全正确，最小值0表示分类效果最差完全错误。

分类报告直接提供了每个分类下的精确率、召回率、F1分数等指标。最下面两行的macro avg和weighted avg分别表示对每个指标的算术平均和加权平均，最后一列的support表示对应的样本数量。

2.ROC曲线 & AUC指标

ROC：Receiver Operating Characteristic。
AUC：Area Under the [ROC] Curve，ROC曲线下的面积。

ROC曲线的绘制中需要用到两个指标：

• 真正率(True Positive Rate/TPR)：在所有真实类别为正类的样本中，模型正确识别为正类的样本所占的比例，也就是把正类样本识别成正类样本的概率。反映了模型识别正类的能力，可以看成是模型在识别正类样本时的收获能力，计算公式$\frac{TP}{TP+FN}$。
• 假正率(False Positive Rate/FPR)：在所有真实类别为负类的样本中，模型错误识别为正类的样本所占的比例，即把负类样本识别为正类样本的概率。反映了模型识别为正类样本时的错误程度，可以理解成模型在识别正类样本时付出的代价，计算公式$\frac{FP}{TN+FP}$。

大多数分类模型都是通过计算出每个样本属于正类的概率，和属于正类的概率阈值进行比较来对样本进行分类的。正类的概率>=阈值，判定为正类，反之判定为负类。

ROC曲线是由不同概率阈值下真正率(y轴)和假正率(x轴)对应的一系列点所构成的曲线，x轴从左到右判定为正类的概率阈值从1到0逐渐递减。ROC曲线用来描述二分类模型预测效果，对于多分类问题，是将关注类视为正类，其他类视为负类。

ROC曲线的具体绘制过程可以理解为：

1. 对于测试集中的每个样本，利用分类器预测其为正类的概率值。
2. 将这些概率值按照从大到小的顺序排列，作为阈值。
3. 对于每个阈值，分别计算真正率和假正率，对应坐标轴上的一个点。
4. 连接这些点。

从真正率和假正率的计算，可以看出曲线越往右，判定为正类的概率阈值越低，那么就有更多的样本被归类到正类当中，因为分母是不变的，分子(TP/FP)随着正类样本增多都会逐渐增大，因此ROC的曲线走势应该是一个从(0, 0)到(1, 1)逐渐上升的曲线。

同时，因为x轴代表了在识别正类时付出的代价，y轴代表了在识别正类时的收获，因此当x值越小，y值越大，即曲线越靠近左上角(0, 1)，说明模型的分类效果越好。

而AUC，是ROC曲线下的面积，它衡量的是模型在所有概率阈值下识别正类时“收获”与“代价”的比重，因此AUC值越大越好，值域范围[0, 1]。
AUC=0.5：模型不具有分类效果，相当于盲猜。
AUC<0.5：分类效果最差，不如盲猜。
AUC>0.5：有一定的分类效果，值越接近1分类效果越好。

下面还是以鸢尾花的数据集为例，通过一个demo对ROC和AUC进行计算和绘制。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, auc# 获取特征值与目标值
data = load_iris()
X, y = data['data'], data['target']# 仅使用两个类别：0 & 1
X = X[y != 2]
y = y[y != 2]# 训练集添加噪声
np.random.seed(42)
noise = np.random.normal(0, 2, (len(X), len(X[0])))
X += noise# 归一化
scaler = MinMaxScaler(feature_range=(-1, 1))
X_scaled = scaler.fit_transform(X)# 划分数据集、创建逻辑回归模型、训练
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
model = LogisticRegression(multi_class='multinomial', max_iter=1000)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)# 获取每个样本预测为正类样本的概率，[:, 0]是负类样本的概率
y_pred_prob = model.predict_proba(X_test)[:, 1]# 计算FPR、TPR和AUC值
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
roc_auc = auc(fpr, tpr)# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, color='green', lw=1, label=f'ROC Curve (AUC={roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='red', lw=1, linestyle='--')
plt.xlim([0.0, 1])
plt.ylim([0.0, 1.05])
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()

output：

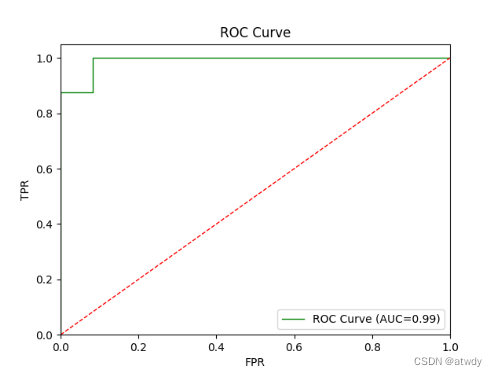
绿线代表ROC曲线，红线相当于盲猜，绿线在红线上方距离红线越远模型分类效果越好。