5.5 树与二叉树的应用
5.5.1 哈夫曼树
结点的权:有某种现实含义的数值。
结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积。
树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL,Weighted Path Length)


哈夫曼树的定义:在含有 n 个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树
哈夫曼树的构造
给定n个权值分别为w1, w2,..., wn的结点,构造哈夫曼树的算法描述如下:
1) 将这n个结点分别作为n棵仅含一个结点的二叉树,构成森林F.
2) 构造一个新结点,从F中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和。
3) 从F中删除刚才选出的两棵树,同时将新得到的树加入F中。
4) 重复步骤2)和3),直至F中只剩下一棵树为止。

![]()
哈夫曼树的性质
1) 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大。
2) 哈夫曼树的结点总数为 2n−1。
3) 哈夫曼树中不存在度为 1 的结点。
4) 哈夫曼树并不唯一,但 WPL 必然相同且为最优。
哈夫曼编码
固定长度编码――每个字符用相等长度的二进制位表示
可变长度编码――允许对不同字符用不等长的二进制位表示
若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码
有哈夫曼树得到哈夫曼编码――字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,根据之前介绍的方法构造哈夫曼树
哈夫曼编码可用于数据压缩
5.5.2_1 并查集
逻辑结构:数据元素之间为“集合”关系
集合的两个基本操作——“并”和“查”
Find ——“查”操作:确定一个指定元 素所属集合
Union ——“并”操作:将两个不想交 的集合合并为一个
注:并查集(Disjoint Set)是逻辑结构——集合的一种具体实现,只进行 “并”和“查”两种基本操作
“并查集”的存储结构
“并查集”的代码实现——初始化
#define SIZE 13
int uFsets [ SIZE]; //集合元素数组
//初始化并查集
void Initial (int S[]){for(int i=0;i<SIZE;i++)s[i]=-1;
}“并查集”的代码实现——并、查
//Find“查”操作,找x所属集合(返回x所属根结点)
int Find (int S[],int x){while(S[x]>=0) //循环寻找x的根x=S[x] ;return x; //根的s[]小于0
)// union“并”操作,将两个集合合并为一个
void union(int S[],int Root1,int Root2){//要求Root1与Root2是不同的集合if(Root1==Root2)return;//将根Root2连接到另一根Root1下面S[Root2]=Root1;Union操作的优化
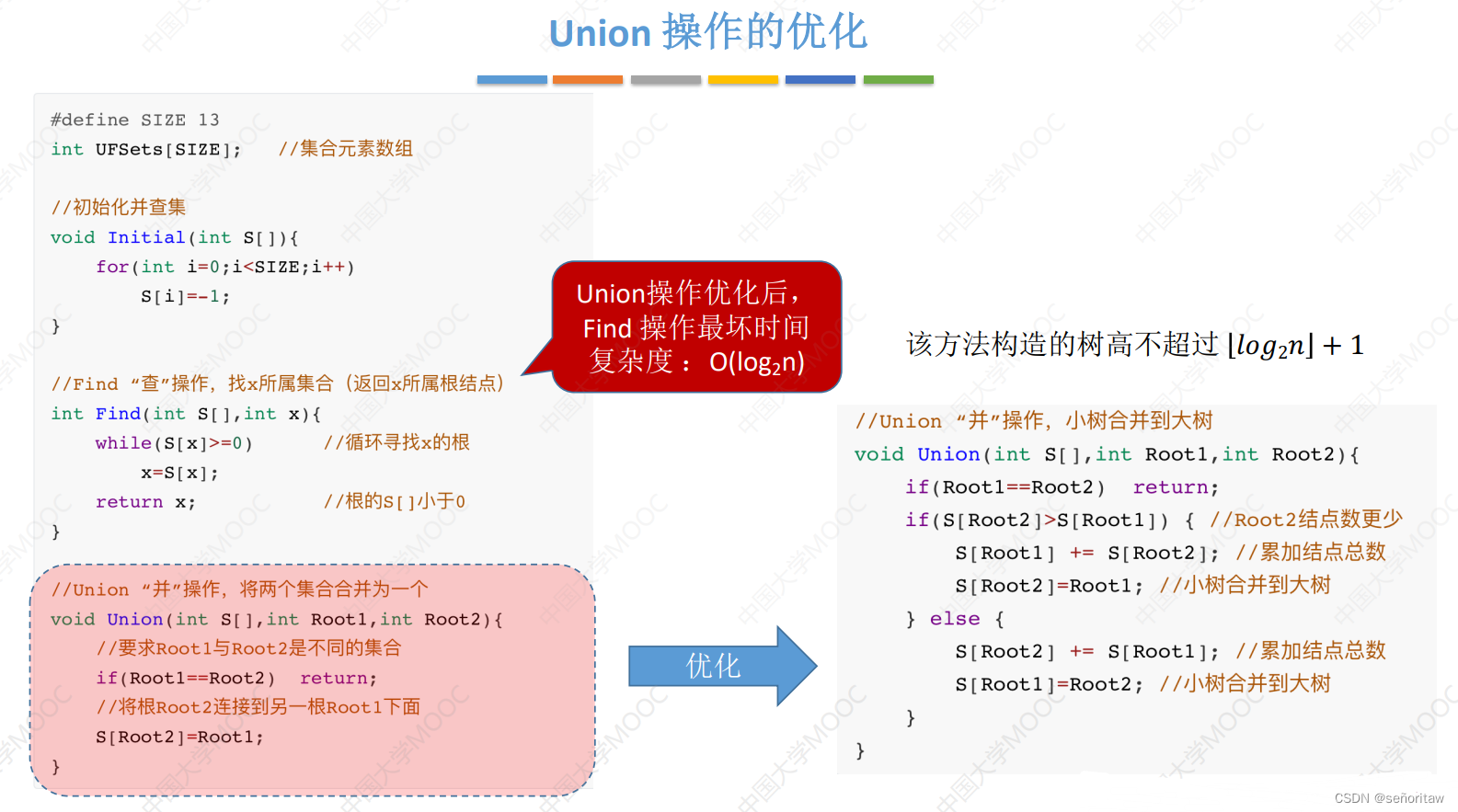
优化思路:在每次Union操作构建树的时候,尽可能让树不长高
①用根节点的绝对值表示树的结点总数
②Union操作,让小树合并到大树
// Union“并”操作,小树合并到大树
void Union (int S[],int Root1,int Root2 ){if(Root1==Root2 ) return;if(S[Root2]>S[Root1]) { //Root2结点数更少S[Root1]+=S[Root2]; //累加结点总数S[Root2]=Root1; //小树合并到大树}else{S[Root2]+=S[Root1]; //累加结点总数S[Root1]=Root2; //小树合并到大树}
}

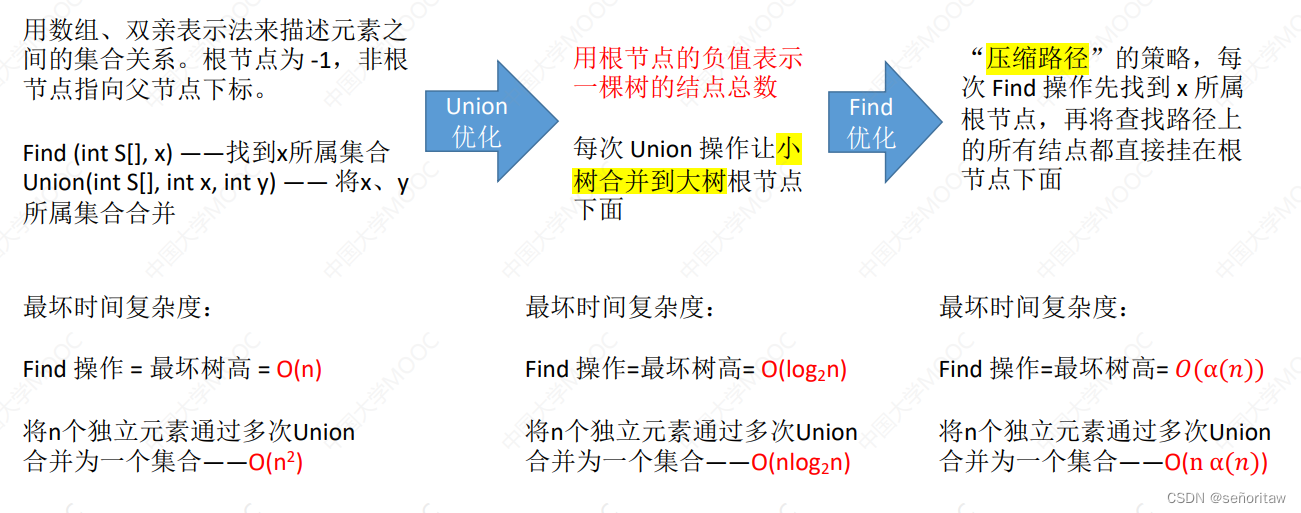
5.5.2_2 并查集的进一步优化
拓展:Find操作的优化(压缩路径)
先找到根结点,再将查找路径上所有结点都挂到根结点下
//Find“查"操作优化,先找到根节点,再进行“压缩路径”
int Find(int S[],int x){int root = x;while(S[root]>=0) root=S[root]; //循环找到根while(x! =root){ //压缩路径int t=S[x]; //t指向x的父节点S[x]=root; //x直接挂到根节点下x=t;}
return root; //返回根节点编号
}




——页面布局方法)




)




—编码基础,数据类型与变量)





