世中逢尔
雨中逢花
目录
计数排序的介绍
代码展示
时间复杂度和空间父复杂度
计数排序的用途
计数排序的局限性

计数排序的介绍
排序原理
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 是一个不比较排序算法,通过计数将时间复杂度降到了O(N)。
排序步骤
第一步⭐
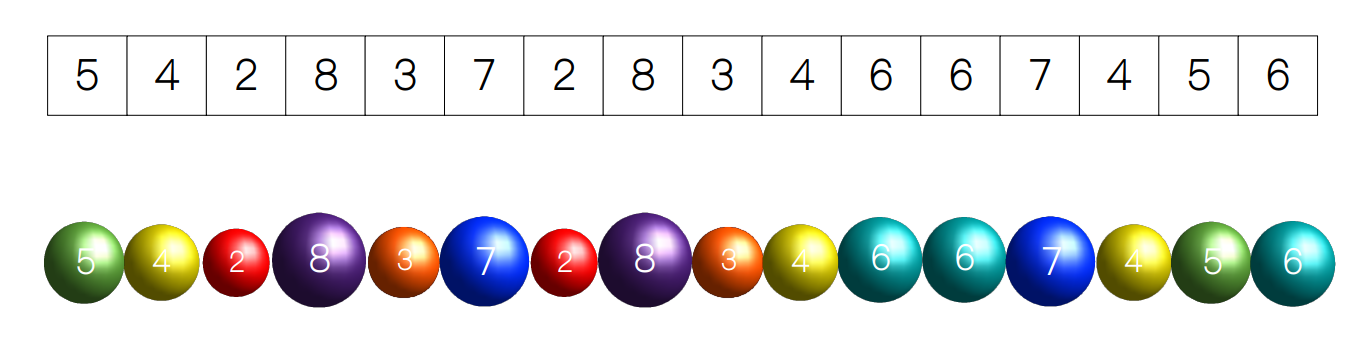
第二步⭐

第三步⭐

第四、五步⭐

第六步⭐
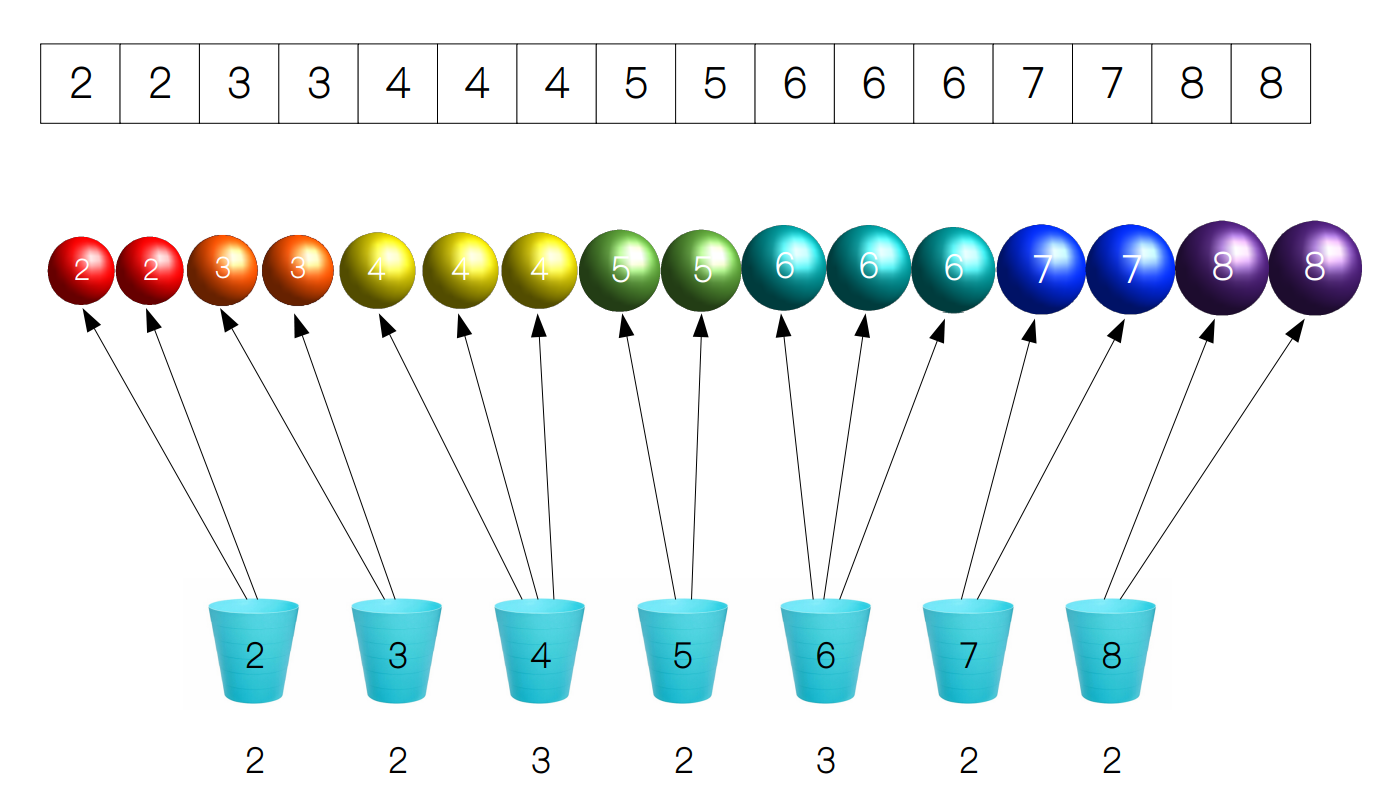
| 第一步 | 找出待排序数组中最大和最小的元素 |
| 第二步 | 根据待排序元素的数值范围大小 range (max-min+1),建立一个 range 大小的频数统计数组count |
| 第三步 | 将统计数组 count 内的元素全部初始化为0 |
| 第四步 | 统计数组中每个值为 i 的元素出现的次数,存入数组count的第 i 项 |
| 第五步 | 对所有的计数累加 |
| 第六步 | 待计数统计完成后遍历count数组,根据次数值来输出原待排序元素值,此时即完成排序 |
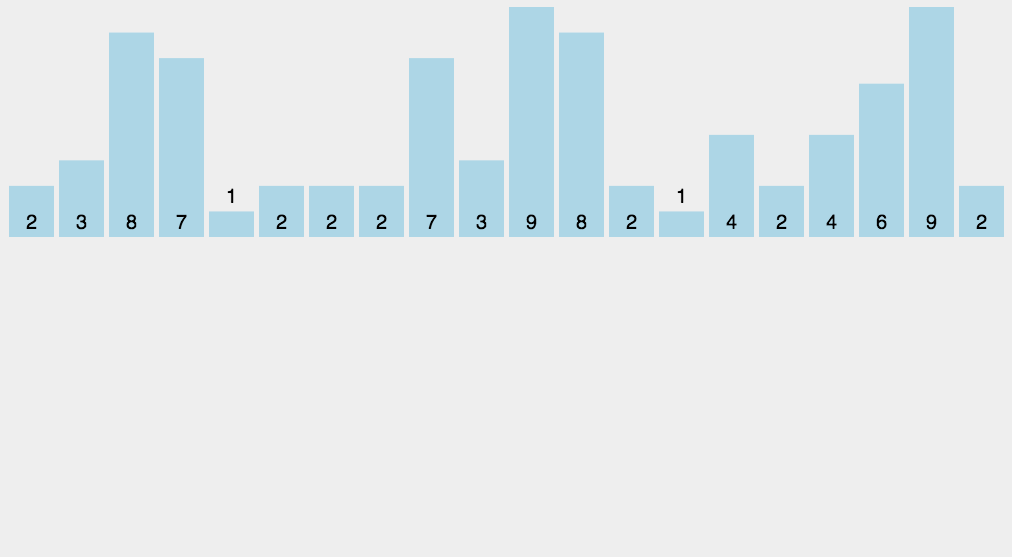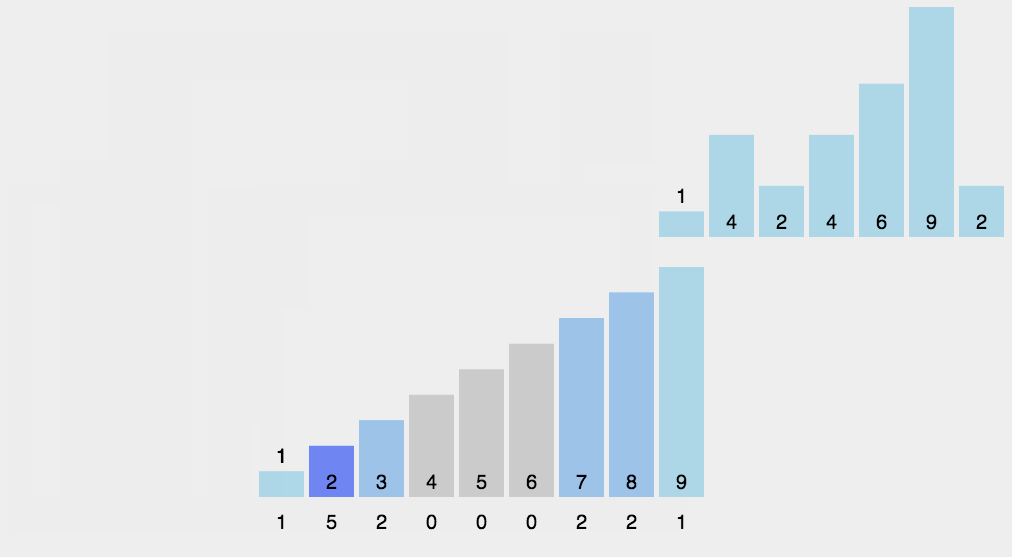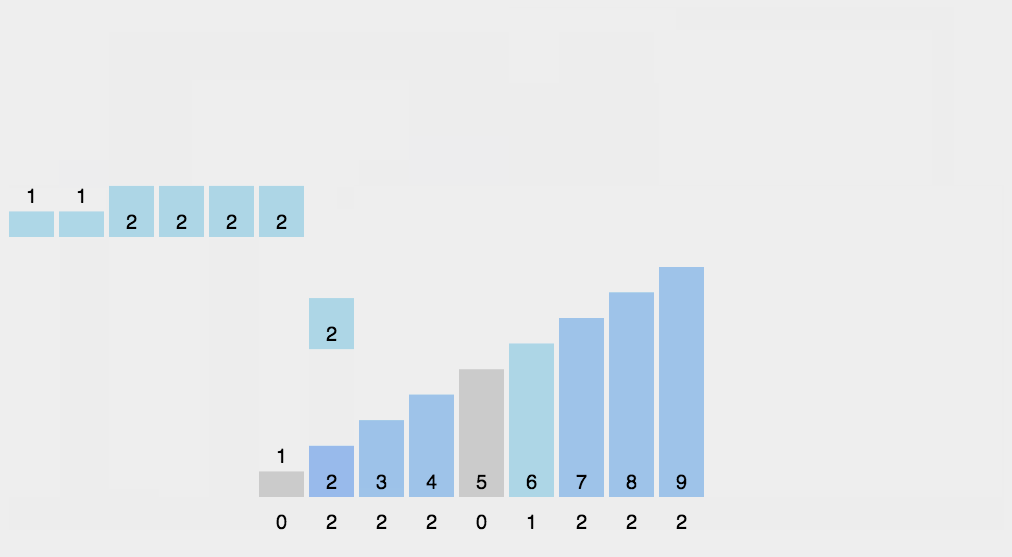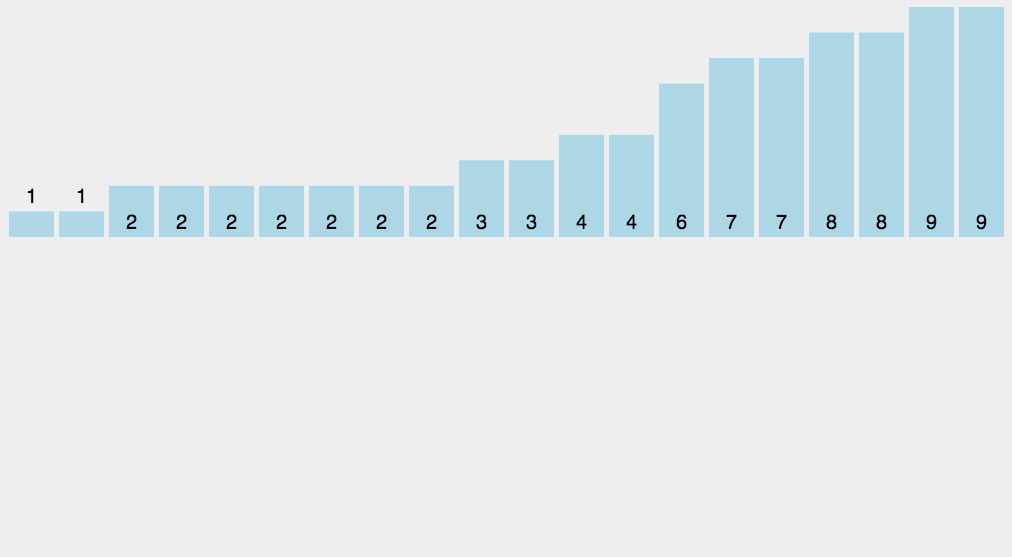
代码展示
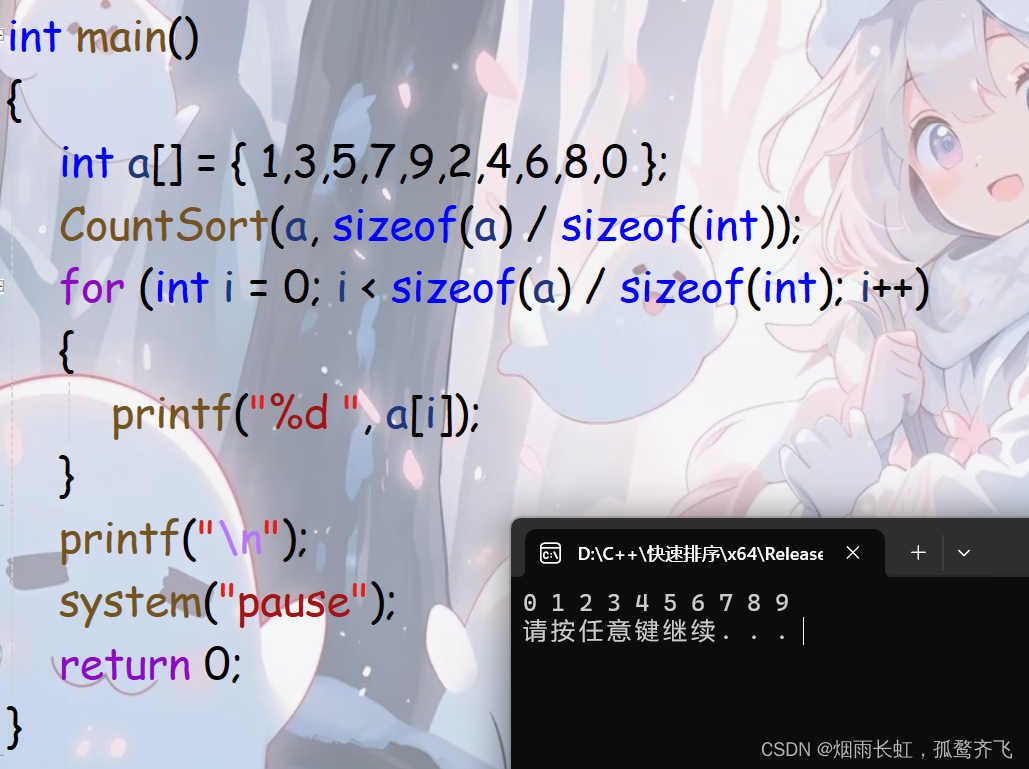
void CountSort(int* a, int n) {int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc");return;}memset(count, 0, sizeof(int) * range);// 统计次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}free(count);count = NULL; }代码测试
时间复杂度和空间父复杂度
时间复杂度:O(n+k)
空间复杂度:O(k)
整个过程需要遍历两次数组,一次是遍历长度为 n 的数组,另一次是从计数器(假设有 k 个计数器)中遍历,因此时间复杂度为 O(n+k)。而在计数排序的过程中用到了长度为 k 的额外数组,故空间复杂度为 O(k)
计数排序的用途
计数排序的一个重要性质就是它是稳定的:具有相同值的元素在输出数组中的相对次序相同。也就是说,对两个相同的数来说,在输入数组中先出现的数,在输出数组中在位于前面。
(在日常中可以运用于相同分数下先交卷的排名靠前等案列中)
计数排序的局限性
| 当数据最大值和最小值差距过大时,并不适用于计数排序 | 比如给定 20 个随机整数,范围在 0 到 1 亿之间,此时如果使用计数排序的话,就需要创建长度为 1 亿的数组,不但严重浪费了空间,而且时间复杂度也随之升高 |
| 当数列元素不是整数时,并不适用于计数排序 | 如果数列中的元素都是小数,比如 3.1415,这则无法创建对应的统计数组,这样显然无法进行计数排序 |
✨计数排序只适用于元素值较为集中的情况
✨计数排序只适用于整型元素







;)




——树森林)





muduo网络库)

