树状数组原理和代码

树状数组

求下标的对应

求i管着的下标的范围

方法：拆掉最右侧的1然后+1 到你自己

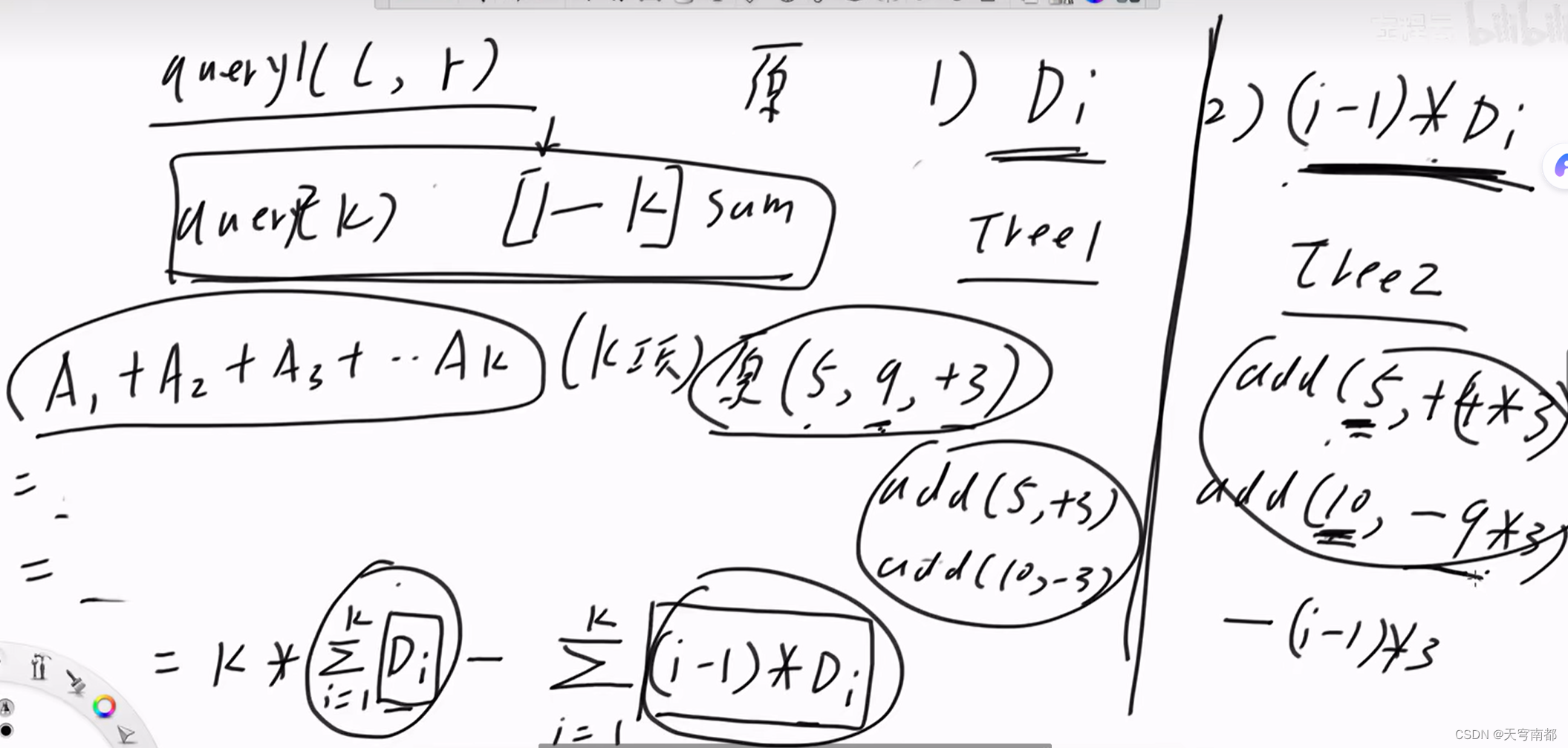
query sum

1-i的和

拆掉最右侧的1 再把下一个数值吸收到sum 重复这个过程直到全变0为止

add

方法：加上最右侧的1 到上限为止

lowbit方法

单点增加范围查询模板

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
#include<vector>
#include<climits>
#include<cmath>
using namespace std;
typedef long long LL;
const int N=5e5+10;
int tree[N];
int n,m;int lowbit(int i){return i&-i;
}void add(int i,int v){while(i<=n){tree[i]+=v;i+=lowbit(i);}
}int sum(int i){int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}int range(int l,int r){return sum(r)-sum(l-1);
}int main() {ios::sync_with_stdio(false); // 可选的，用于加快I/Ocin.tie(0);while (cin >> n >> m) {for (int i = 1, v; i <= n; i++) {cin >> v;add(i, v);}for (int i = 1, a, b, c; i <= m; i++) {cin >> a >> b >> c;if (a == 1) {add(b, c);} else {cout << range(b, c) << '\n';}}}return 0;
}

范围增加单点查询的模板

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
#include<vector>
#include<climits>
#include<cmath>
using namespace std;
typedef long long LL;
const int N=5e5+10;
int tree[N];
int n,m;int lowbit(int i){return i&-i;
}void add(int i,int v){while(i<=n){tree[i]+=v;i+=lowbit(i);}
}int sum(int i){int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}int range(int l,int r){return sum(r)-sum(l-1);
}int main() {while (cin >> n >> m) {for (int i = 1, v; i <= n; i++) {cin >> v;add(i, v);add(i + 1, -v);}for (int i = 1; i <= m; i++) {int op;cin >> op;if (op == 1) {int l, r, v;cin >> l >> r >> v;add(l, v);add(r + 1, -v);} else {int index;cin >> index;cout << sum(index) << '\n';}}}return 0;
}

树状数组实现范围增加范围查询

#include <iostream>
using namespace std;const int MAXN = 100001;
long long info1[MAXN]; // 维护原始数组的差分信息：Di
long long info2[MAXN]; // 维护原始数组的差分加工信息：(i-1) * Di
int n, m;int lowbit(int i) {return i & -i;
}void add(long long tree[], int i, long long v) {while (i <= n) {tree[i] += v;i += lowbit(i);}
}long long sum(long long tree[], int i) {long long ans = 0;while (i > 0) {ans += tree[i];i -= lowbit(i);}return ans;
}void rangeAdd(int l, int r, long long v) {add(info1, l, v);add(info1, r + 1, -v);add(info2, l, (l - 1) * v);add(info2, r + 1, -(r * v));
}long long rangeQuery(int l, int r) {return sum(info1, r) * r - sum(info2, r) - sum(info1, l - 1) * (l - 1) + sum(info2, l - 1);
}int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n >> m;long long cur;for (int i = 1; i <= n; ++i) {cin >> cur;rangeAdd(i, i, cur);}int op, l, r;long long v;for (int i = 1; i <= m; ++i) {cin >> op;if (op == 1) {cin >> l >> r >> v;rangeAdd(l, r, v);} else {cin >> l >> r;cout << rangeQuery(l, r) << '\n';}}return 0;
}

相关题目

逆序对

归并分治法

#include <iostream>
#include <vector>
using namespace std;const int MAXN = 500001;
int arr[MAXN];
int help[MAXN];
int n;
long long merge(int l, int m, int r);long long f(int l, int r) {if (l == r) {return 0;}int m = (l + r) / 2;return f(l, m) + f(m + 1, r) + merge(l, m, r);
}long long merge(int l, int m, int r) {long long ans = 0;// 统计逆序对数量for (int i = m, j = r; i >= l; i--) {while (j >= m + 1 && arr[i] <= arr[j]) {j--;}ans += j - m;}// 归并排序，让arr[l...r]变成有序int i = l, a = l, b = m + 1;while (a <= m && b <= r) {help[i++] = arr[a] <= arr[b] ? arr[a++] : arr[b++];}while (a <= m) {help[i++] = arr[a++];}while (b <= r) {help[i++] = arr[b++];}for (i = l; i <= r; i++) {arr[i] = help[i];}return ans;
}int main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> arr[i];}cout << f(1, n) << '\n';return 0;
}

树状数组解法

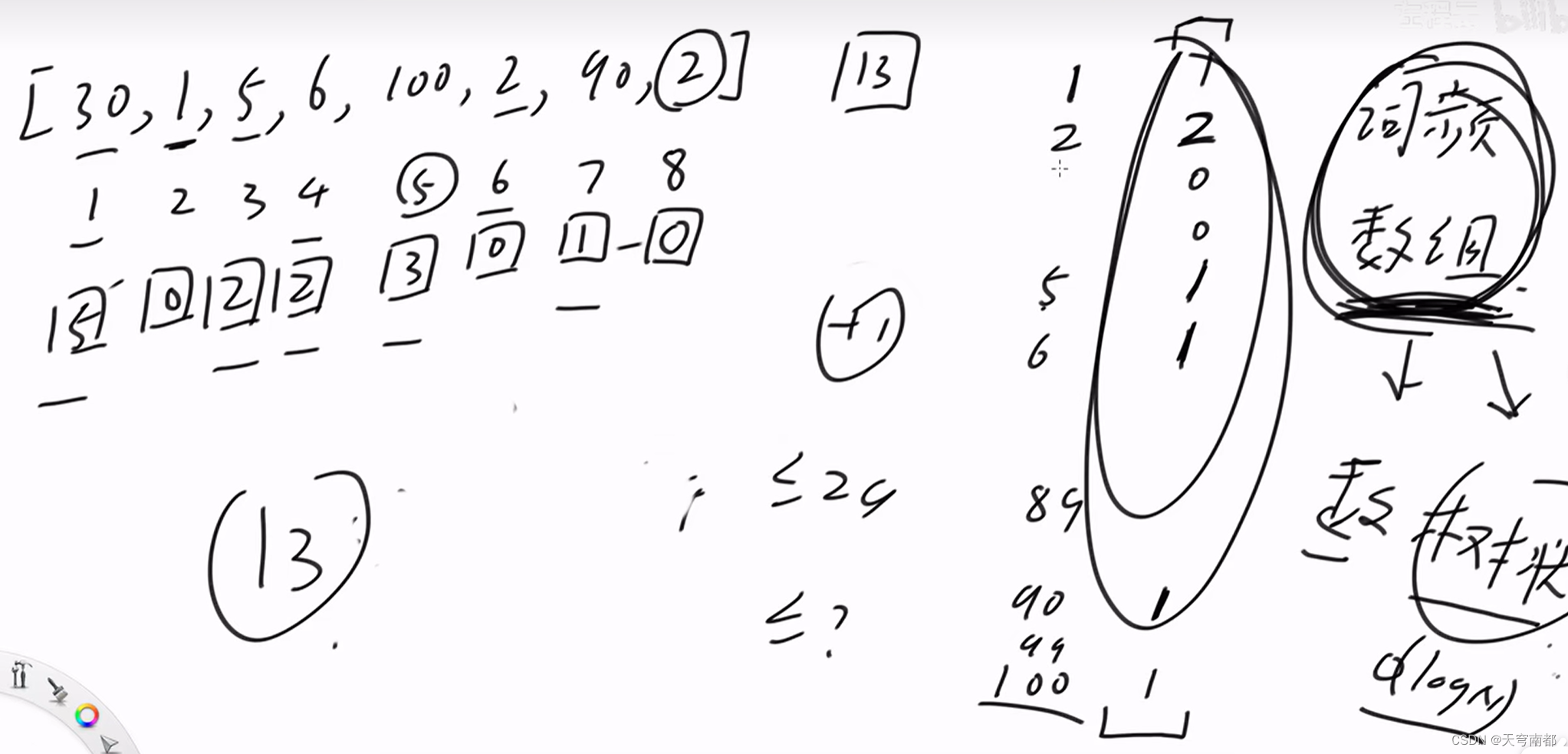
去重+离散化

#include <iostream>
#include <algorithm>
using namespace std;const int MAXN = 500001;
int arr[MAXN];
int sortArr[MAXN]; // 用于排序和去重的数组
int tree[MAXN]; // 树状数组
int n, m; // n为数组长度，m为离散化后的值域大小int lowbit(int x) {return x & (-x);
}void add(int idx, int val) {while (idx <= m) {tree[idx] += val;idx += lowbit(idx);}
}long long sum(int idx) {long long res = 0;while (idx > 0) {res += tree[idx];idx -= lowbit(idx);}return res;
}// 离散化函数，将数组arr中的值映射到1~m
void discretization() {sort(sortArr + 1, sortArr + n + 1);m = unique(sortArr + 1, sortArr + n + 1) - (sortArr + 1); // unique返回去重后的尾后迭代器for (int i = 1; i <= n; ++i) {arr[i] = lower_bound(sortArr + 1, sortArr + m + 1, arr[i]) - sortArr;}
}long long compute() {long long ans = 0;for (int i = n; i >= 1; --i) {ans += sum(arr[i] - 1);add(arr[i], 1);}return ans;
}int main() {ios::sync_with_stdio(false); // 关闭同步cin.tie(0); // 解除cin和cout的绑定cout.tie(0);cin >> n;for (int i = 1; i <= n; ++i) {cin >> arr[i];sortArr[i] = arr[i];}discretization(); // 离散化处理cout << compute() << endl; // 计算逆序对数量并输出return 0;
}

上升三元组

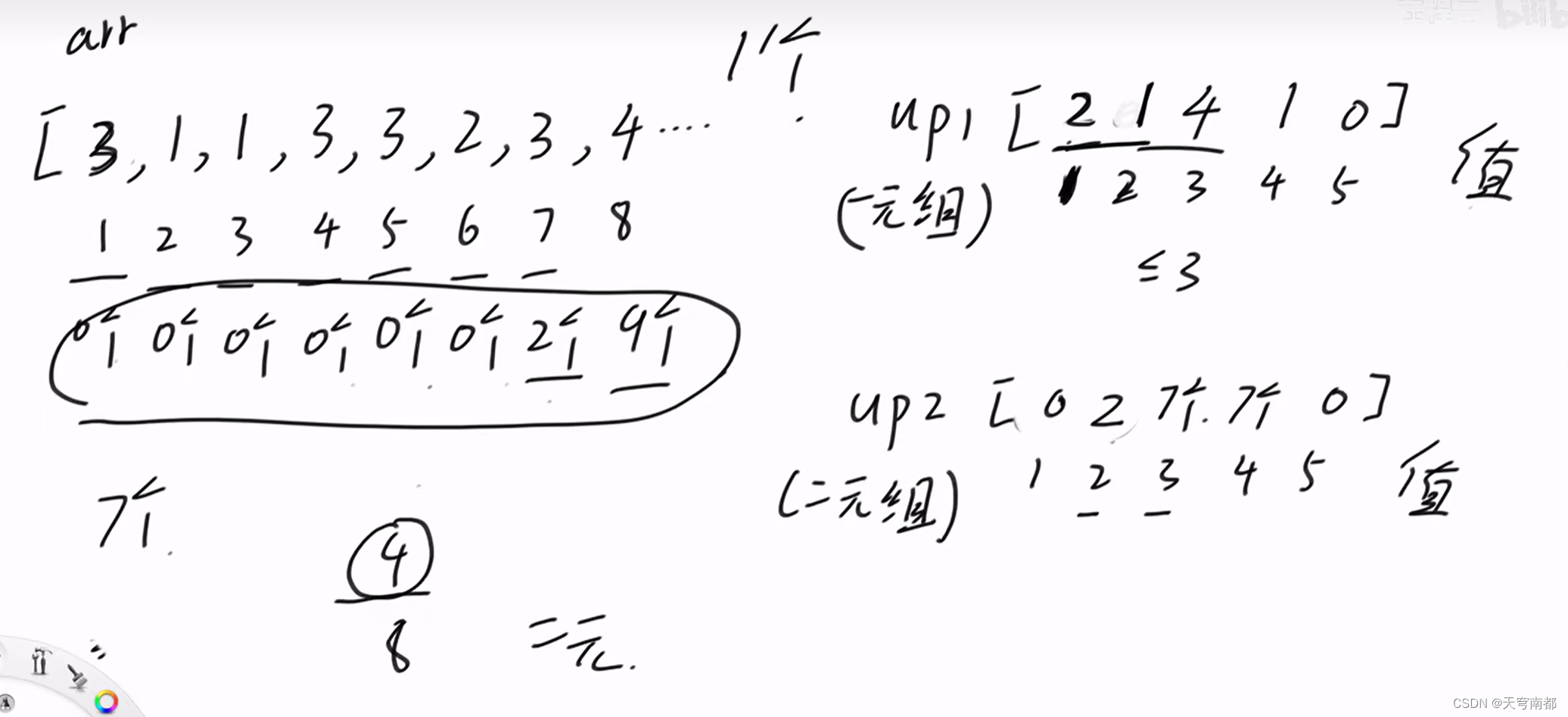
#include <iostream>
#include <algorithm>
#include <vector>using namespace std;const int MAXN = 30001;
int arr[MAXN], sortArr[MAXN];
long long tree1[MAXN], tree2[MAXN];
int n, m;int lowbit(int i) {return i & -i;
}void add(long long tree[], int i, long long c) {while (i <= m) {tree[i] += c;i += lowbit(i);}
}long long sum(long long tree[], int i) {long long ans = 0;while (i > 0) {ans += tree[i];i -= lowbit(i);}return ans;
}long long compute() {copy(arr + 1, arr + n + 1, sortArr + 1);sort(sortArr + 1, sortArr + n + 1);m = unique(sortArr + 1, sortArr + n + 1) - (sortArr + 1);for (int i = 1; i <= n; i++) {// Using lower_bound to replace the manual rank functionarr[i] = lower_bound(sortArr + 1, sortArr + m + 1, arr[i]) - sortArr;}long long ans = 0;for (int i = 1; i <= n; i++) {ans += sum(tree2, arr[i] - 1);add(tree1, arr[i], 1);add(tree2, arr[i], sum(tree1, arr[i] - 1));}return ans;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cin >> n;for (int i = 1; i <= n; i++) {cin >> arr[i];}cout << compute() << endl;return 0;
}

最长递增子序列个数

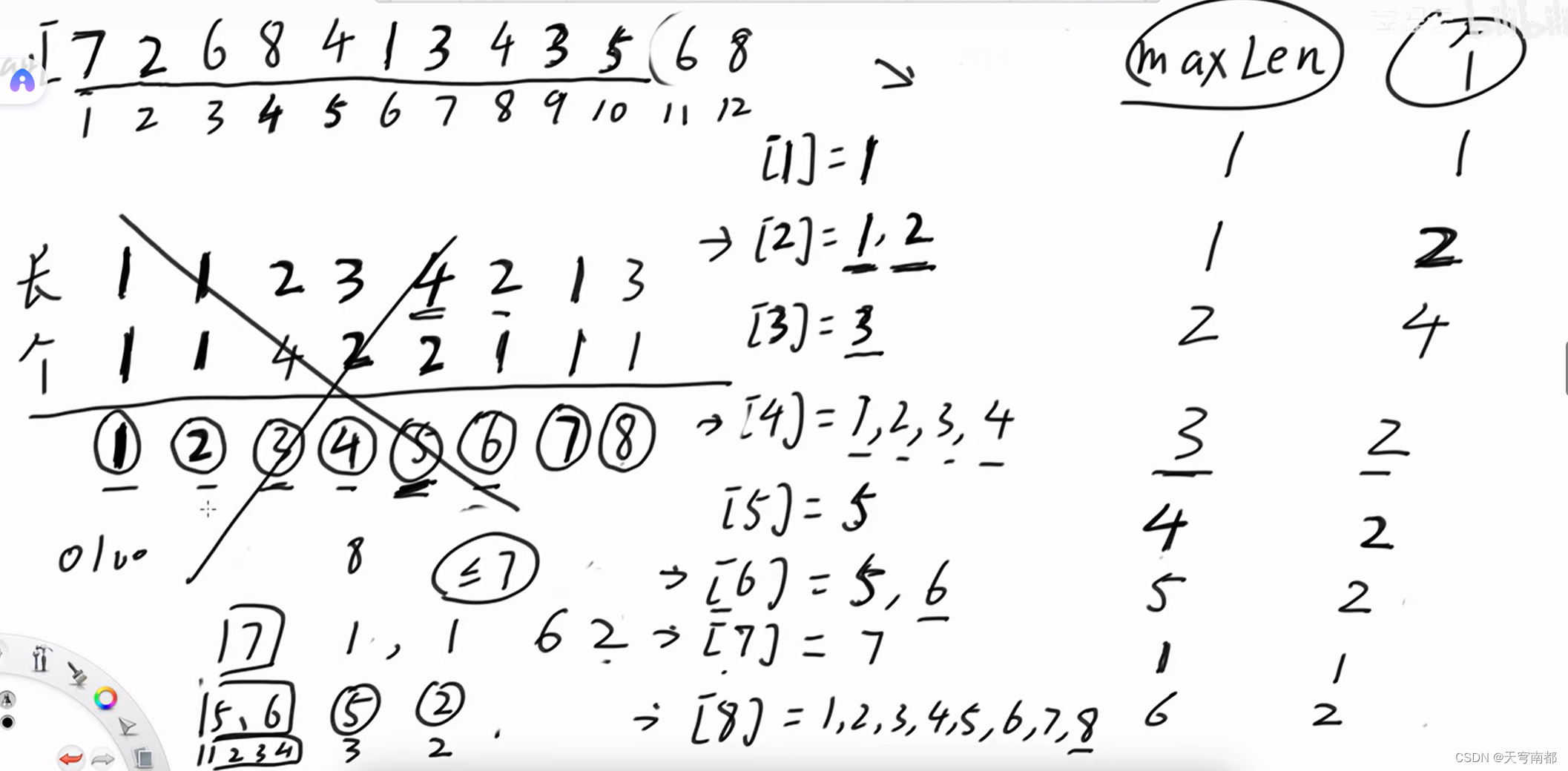
673. 最长递增子序列的个数

#include <vector>
#include <algorithm>
#include <numeric> // 用于iota函数
using namespace std;class Solution {
public:static const int MAXN = 2001; // 设置最大数值范围vector<int> treeMaxLen = vector<int>(MAXN, 0); // 以数值i结尾的最长递增子序列的长度vector<int> treeMaxLenCnt = vector<int>(MAXN, 0); // 以数值i结尾的最长递增子序列的个数int m; // 数组去重排序后的长度int lowbit(int i) {return i & (-i);}void query(int i, int& maxLen, int& maxLenCnt) {maxLen = maxLenCnt = 0;while (i > 0) {if (treeMaxLen[i] == maxLen) {maxLenCnt += treeMaxLenCnt[i];} else if (treeMaxLen[i] > maxLen) {maxLen = treeMaxLen[i];maxLenCnt = treeMaxLenCnt[i];}i -= lowbit(i);}}void add(int i, int len, int cnt) {while (i <= m) {if (treeMaxLen[i] == len) {treeMaxLenCnt[i] += cnt;} else if (treeMaxLen[i] < len) {treeMaxLen[i] = len;treeMaxLenCnt[i] = cnt;}i += lowbit(i);}}int findNumberOfLIS(vector<int>& nums) {if (nums.empty()) return 0;vector<int> sortedNums(nums.begin(), nums.end());sort(sortedNums.begin(), sortedNums.end());auto it = unique(sortedNums.begin(), sortedNums.end()); // 去重，it指向去重后新的末尾m = distance(sortedNums.begin(), it); // 使用迭代器之间的距离作为去重后数组的长度// 根据去重后的长度调整树状数组的大小treeMaxLen.assign(m + 1, 0);treeMaxLenCnt.assign(m + 1, 0);for (int num : nums) {// 注意这里的lower_bound的范围，应当是begin()到itint i = lower_bound(sortedNums.begin(), it, num) - sortedNums.begin() + 1; // 获取排名（1-based）int maxLen, maxLenCnt;query(i - 1, maxLen, maxLenCnt);add(i, maxLen + 1, maxLenCnt == 0 ? 1 : maxLenCnt);}int totalMaxLen = 0, totalCount = 0;query(m, totalMaxLen, totalCount);return totalCount;
}};

P1972 [SDOI2009] HH的项链

每种颜色只留最右边的

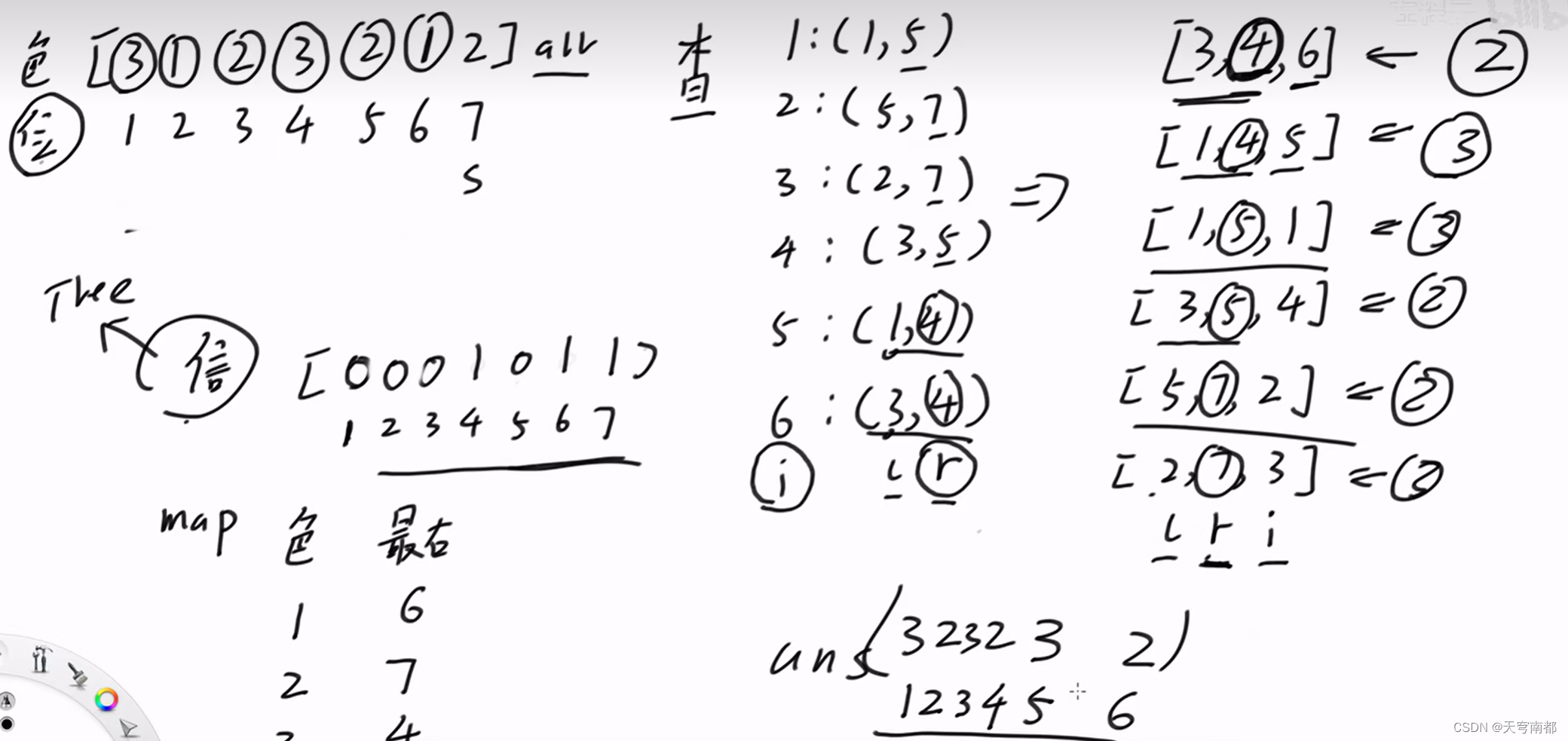
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstdio>using namespace std;const int MAXN = 1000010;
int arr[MAXN], ans[MAXN], map[MAXN], tree[MAXN], n, m;struct Query {int l, r, idx;Query(int l = 0, int r = 0, int idx = 0) : l(l), r(r), idx(idx) {}
};vector<Query> queries(MAXN);int lowbit(int i) {return i & -i;
}void add(int i, int v) {while (i <= n) {tree[i] += v;i += lowbit(i);}
}int sum(int i) {int ans = 0;while (i > 0) {ans += tree[i];i -= lowbit(i);}return ans;
}int range(int l, int r) {return sum(r) - sum(l - 1);
}void compute() {sort(queries.begin() + 1, queries.begin() + m + 1, [](const Query& a, const Query& b) {return a.r < b.r;});for (int s = 1, q = 1; q <= m; q++) {int r = queries[q].r;for (; s <= r; s++) {if (map[arr[s]] != 0) {add(map[arr[s]], -1);}add(s, 1);map[arr[s]] = s;}ans[queries[q].idx] = range(queries[q].l, r);}
}int main() {scanf("%d", &n);for (int i = 1; i <= n; i++) {scanf("%d", &arr[i]);}scanf("%d", &m);for (int i = 1; i <= m; i++) {int l, r;scanf("%d %d", &l, &r);queries[i] = Query(l, r, i);}compute();for (int i = 1; i <= m; i++) {printf("%d\n", ans[i]);}return 0;
}