问题预览

1. 模型的参数（w和b）有什么作用？
2. 不同的w和b对线性回归模型有什么影响？
3. 训练集里的y和线性回归模型预测的y（y帽）的区别是什么？
4. 成本函数的作用是什么？
5. 成本函数的公式是什么？
6. 成本函数是如何计算的？
7. 成本函数最小化意味着什么？

解读

（笔者备注：成本函数和代价函数是一个意思。）

• 参数w和b：为了使模型预测的y值更准确，我们需要调整w和b的值。w和b也叫做系数或权重。例如，我们需要挑选合适的w和b，来让f(x)这条直线大致通过或接近训练集数据。
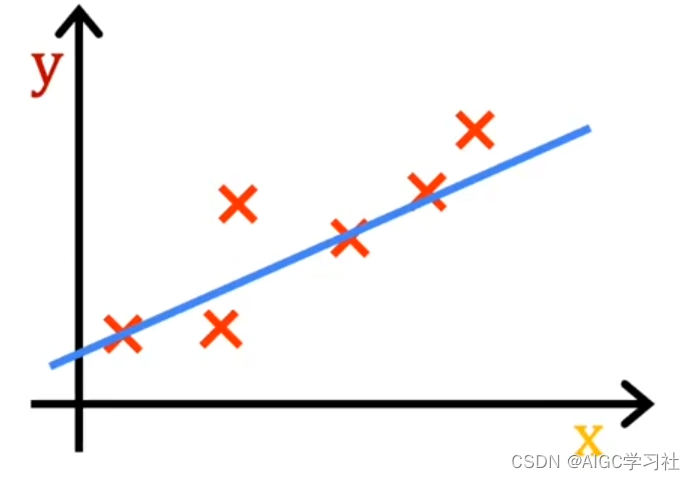
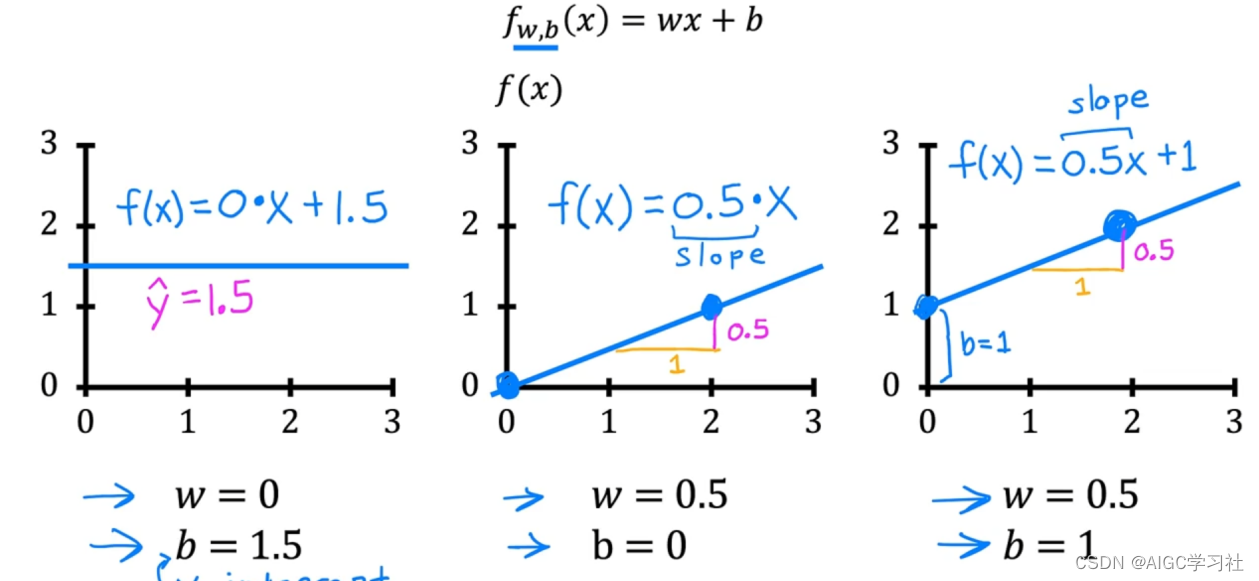
• 不同的w和b：设置不同的w和b，我们会得到不同的f(x)函数模型，因此计算出的结果也会不同。
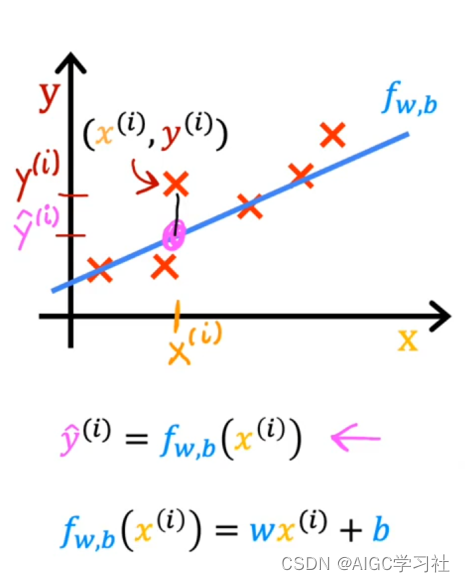
• y和y帽：图里红色的×是训练集的数据，x是特征，y是目标变量，而通过蓝色线条（线性回归模型）计算出的y，我们叫做y帽（预测值）。
• 代价函数：我们的目的是为了找到合适的w和b，前几点都在看w和b对线性回归的影响，而通过代价函数的计算，我们就能够找到合适的w和b。
• 代价函数的公式：Σ是求和的意思，对符号后面的公式求和，从i=1到i=m，有几次就要计算几次，然后累积所有计算结果。
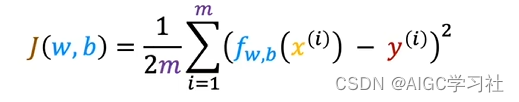
• 计算代价函数：我们先计算第一行训练样本，f(w,b)就是通过线性回归，计算的第一行训练样本y帽（预测值），预测值在减去第一行训练样本的目标变量y，也就是真实训练集的y，然后对这个差值求平方。然后在计算第二行，第三行，一直到第m行，每次计算的结果都要一直记录累加，然后最终结果乘以1/2m（m是样本数量）。
• 代价函数最小值：将我们找到的w和b代入到成本函数中，如果成本函数能计算出最小值，表示我们当前的w和b的值是最合适的。

总结

想要比较完美的拟合数据，我们需要找到合适的w和b来构建线性回归模型。

通过将当前w和b代入到成本函数，我们可以通过成本函数的值来判断w和b是否合适，如果成本函数是最小值，则w和b的参数是最合适的。

成本函数的计算方式是每一行的训练样本都要计算，然后累加每一行的结果。

后续课程会详细讲解代价函数以及如何计算成本函数的最小值。