---------------🎈🎈题目链接🎈🎈-------------------

解法

😒: 我的代码实现============>

动规五部曲

✒️确定dp数组以及下标的含义

dp[i] 表示跳跃到第 i 层，需要的最少花费总和

✒️确定递推公式

可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。
dp[i-1] ：表示跳到 i -1 层需要的花费
dp[i-2] ：表示跳到 i -2 层需要的花费
从dp[i-1] 跳到 dp[i] 层需要的花费：dp[i-1] + cost[i-1]
从dp[i-2] 跳到 dp[i] 层需要的花费：dp[i-2] + cost[i-2]

那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢？——选小的
因此: dp[i] = Min( dp[i-1] + cost[i-1] ， dp[i-2] + cost[i-2] )

✒️dp数组初始化

在第0层，和第1层的时候不花费。
如果要跳走，那就需要花费
所以初始化dp[0] = 0 , dp[1] = 1

✒️确定遍历顺序

从前到后

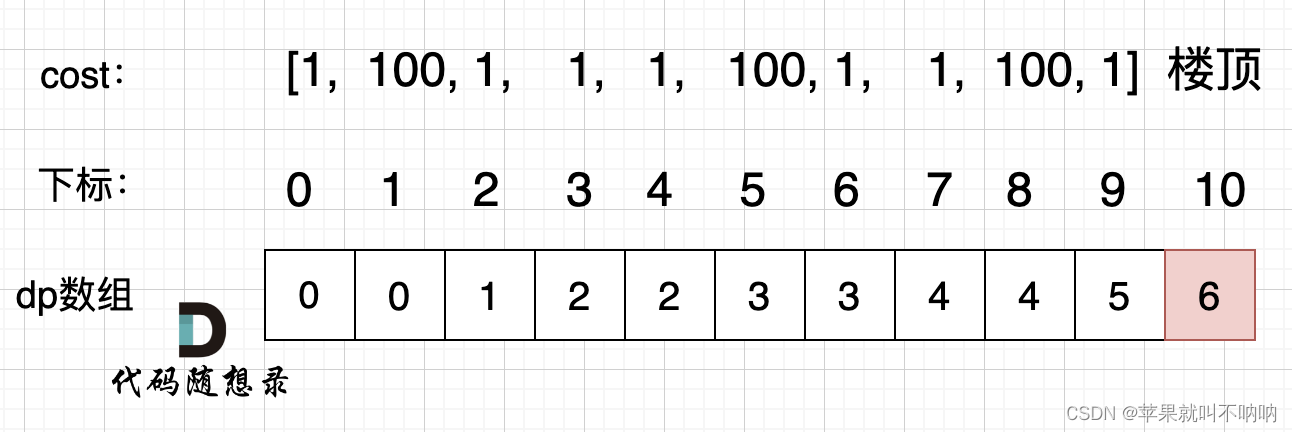
✒️举例推导dp数组

时间复杂度O(N)
空间复杂度O(N)

📘代码

class Solution {public int minCostClimbingStairs(int[] cost) {// 动态规划// dp数组：dp[i] 到达第i台阶所花费的最少费用为dp[i]int[] dp = new int[cost.length+1];// 到达第0层和第1层不需要花费，所以初始化为：dp[0] = 0;dp[1] = 0;for(int i = 2; i < cost.length+1; i++){ // 顺序遍历 从2开始到到达楼梯顶部（cost.length+1）dp[i] = Math.min( (dp[i-1] + cost[i-1]), (dp[i-2] + cost[i-2]) );}return dp[cost.length];}