给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

示例 1：

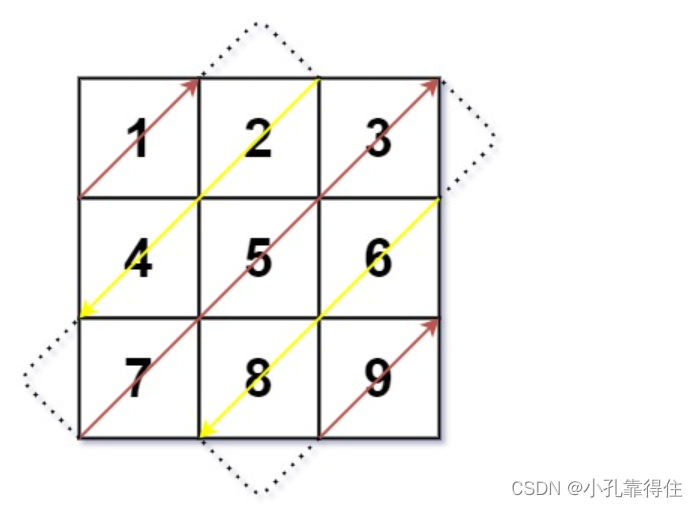
输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,4,7,5,3,6,8,9]
示例 2：

输入：mat = [[1,2],[3,4]]
输出：[1,2,3,4]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 10^4
• 1 <= m * n <= 10^4
• 10 ^ 5 <= mat[i][j] <= 10^5

代码实现

public static int[] findDiagonalOrder(int[][] matrix) {if (matrix.length == 0) {return new int[0]; // 如果矩阵为空，则返回空数组}int m = matrix.length; // 获取矩阵的行数int n = matrix[0].length; // 获取矩阵的列数int[] ans = new int[m * n]; // 初始化存放结果的一维数组int count = n + m - 1; // 对角线方向次数，即矩阵的行数加列数减1int row = 0, col = 0, Index = 0; // 初始化行标记、列标记和存放数组的索引for (int i = 0; i < count; i++) { // 循环遍历对角线次数if (i % 2 == 0) { // 如果当前是偶数次对角线，则从右上角开始遍历while (row >= 0 && col < n) { // 右上遍历ans[Index] = matrix[row][col]; // 将矩阵中的元素存入结果数组Index++; // 索引后移row--; // 行减一col++; // 列加一}if (col < n) { // 判断是否越界row++; // 如果不越界，正常行加一} else { // 如果越界，则是最长的左下对角线row += 2; // 行加二col--; // 列减一}} else { // 如果当前是奇数次对角线，则从左下角开始遍历while (row < m && col >= 0) { // 左下遍历，与右上相反ans[Index] = matrix[row][col]; // 将矩阵中的元素存入结果数组Index++; // 索引后移row++; // 行加一col--; // 列减一}if (row < m) { // 判断是否越界col++; // 如果不越界，正常列加一} else { // 如果越界，则是最长的右上对角线row--; // 行减一col += 2; // 列加二}}}return ans; // 返回存放结果的数组
}

详细说明：

• 首先检查输入矩阵是否为空，如果为空则直接返回一个空数组。
• 然后获取矩阵的行数 m 和列数 n。
• 初始化存放结果的一维数组 ans，其长度为 m * n。
• 初始化对角线方向的次数 count，即矩阵的行数加列数减1。
• 初始化行标记 row、列标记 col 和存放数组的索引 Index，分别表示当前位置的行、列以及存放数组的索引。
• 开始对角线循环，循环次数为 count。
• 在循环中，根据当前对角线次数的奇偶性，选择从右上或左下开始遍历矩阵。
• 在遍历过程中，根据遍历的方向将矩阵中的元素存入结果数组，并更新行标记和列标记。
• 在遍历完成后，返回存放结果的数组 ans。